
Previous in Relation and Functions Next in Relation and Functions
Question Number 57412 by Abdo msup. last updated on 03/Apr/19
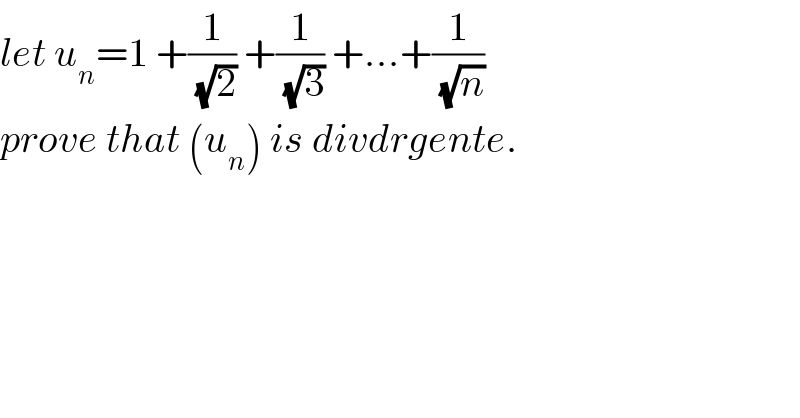
$${let}\:{u}_{{n}} =\mathrm{1}\:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:+\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:+...+\frac{\mathrm{1}}{\sqrt{{n}}} \\ $$$${prove}\:{that}\:\left({u}_{{n}} \right)\:{is}\:{divdrgente}. \\ $$
Commented by maxmathsup by imad last updated on 07/Apr/19
![let f(x)=(√x) ∃c ∈]k,k+1[ /f(k+1)−f(k)=(k+1−k)f^′ (c)⇒(√(k+1)) −(√k)=(1/(2(√c))) we have k<c<k+1 ⇒(√k)<(√c)<(√(k+1)) ⇒(1/(2(√c))) <(1/(2(√k))) ⇒ (1/(2(√k))) >(√(k+1))−(√k) ⇒ Σ_(k=1) ^n (1/(√k)) >2 Σ_(k=1) ^n {(√(k+1))−(√k)) ⇒ U_(n ) > 2{(√(n+1))−1} →+∞ (n→+∞) ⇒U_n diverges and lim_(n→+∞) U_n =+∞ .](Q57532.png)
$$\left.{let}\:{f}\left({x}\right)=\sqrt{{x}}\:\:\:\exists{c}\:\in\right]{k},{k}+\mathrm{1}\left[\:\:\:/{f}\left({k}+\mathrm{1}\right)−{f}\left({k}\right)=\left({k}+\mathrm{1}−{k}\right){f}^{'} \left({c}\right)\Rightarrow\sqrt{{k}+\mathrm{1}}\:−\sqrt{{k}}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{c}}}\right. \\ $$$${we}\:{have}\:\:\:\:{k}<{c}<{k}+\mathrm{1}\:\Rightarrow\sqrt{{k}}<\sqrt{{c}}<\sqrt{{k}+\mathrm{1}}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{2}\sqrt{{c}}}\:<\frac{\mathrm{1}}{\mathrm{2}\sqrt{{k}}}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\sqrt{{k}}}\:>\sqrt{{k}+\mathrm{1}}−\sqrt{{k}}\:\Rightarrow\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\sqrt{{k}}}\:>\mathrm{2}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\left\{\sqrt{{k}+\mathrm{1}}−\sqrt{{k}}\right)\:\Rightarrow \\ $$$${U}_{{n}\:} \:>\:\mathrm{2}\left\{\sqrt{{n}+\mathrm{1}}−\mathrm{1}\right\}\:\rightarrow+\infty\:\left({n}\rightarrow+\infty\right)\:\Rightarrow{U}_{{n}} \:{diverges}\:{and}\:{lim}_{{n}\rightarrow+\infty} {U}_{{n}} =+\infty\:. \\ $$
