
Previous in Relation and Functions Next in Relation and Functions
Question Number 32335 by abdo imad last updated on 23/Mar/18
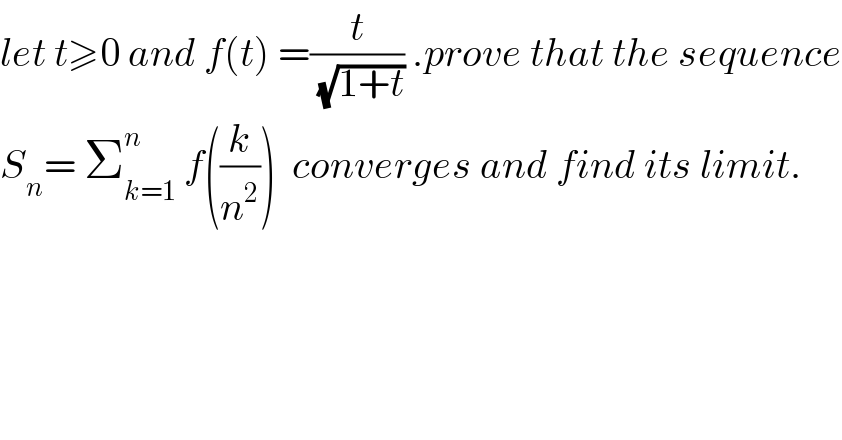
$${let}\:{t}\geqslant\mathrm{0}\:{and}\:{f}\left({t}\right)\:=\frac{{t}}{\sqrt{\mathrm{1}+{t}}}\:.{prove}\:{that}\:{the}\:{sequence} \\ $$$${S}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}} \:{f}\left(\frac{{k}}{{n}^{\mathrm{2}} }\right)\:\:{converges}\:{and}\:{find}\:{its}\:{limit}. \\ $$
