
Question Number 33702 by math khazana by abdo last updated on 22/Apr/18
![let p(x) =a_0 +a_1 x +a_2 x^2 +...a_n x^n prove that a_k = ((p^((k)) (0))/(k!)) ∀ k ∈[[0,n]] .](Q33702.png)
$${let}\:{p}\left({x}\right)\:={a}_{\mathrm{0}} \:+{a}_{\mathrm{1}} {x}\:+{a}_{\mathrm{2}} {x}^{\mathrm{2}} \:+...{a}_{{n}} {x}^{{n}} \\ $$$${prove}\:{that}\:\:{a}_{{k}} =\:\frac{{p}^{\left({k}\right)} \left(\mathrm{0}\right)}{{k}!}\:\:\forall\:{k}\:\in\left[\left[\mathrm{0},{n}\right]\right]\:. \\ $$
Commented by math khazana by abdo last updated on 29/Apr/18
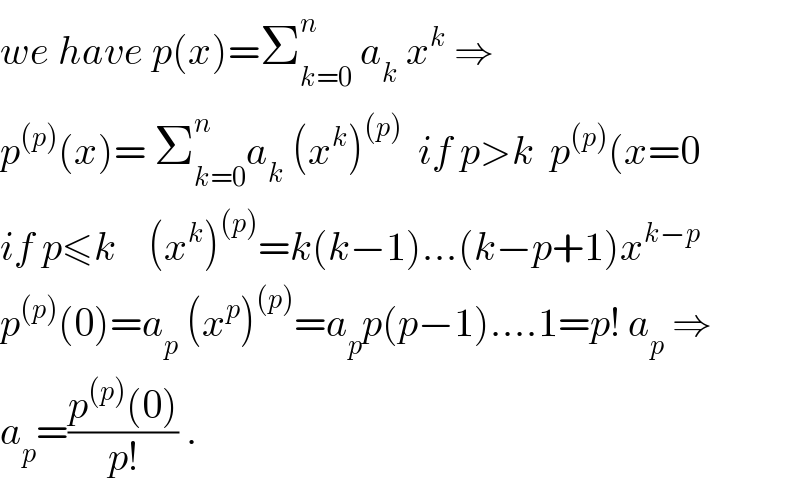
$${we}\:{have}\:{p}\left({x}\right)=\sum_{{k}=\mathrm{0}} ^{{n}} \:{a}_{{k}} \:{x}^{{k}} \:\Rightarrow \\ $$$${p}^{\left({p}\right)} \left({x}\right)=\:\sum_{{k}=\mathrm{0}} ^{{n}} {a}_{{k}} \:\left({x}^{{k}} \right)^{\left({p}\right)} \:\:{if}\:{p}>{k}\:\:{p}^{\left({p}\right)} \left({x}=\mathrm{0}\right. \\ $$$${if}\:{p}\leqslant{k}\:\:\:\:\left({x}^{{k}} \right)^{\left({p}\right)} ={k}\left({k}−\mathrm{1}\right)...\left({k}−{p}+\mathrm{1}\right){x}^{{k}−{p}} \\ $$$${p}^{\left({p}\right)} \left(\mathrm{0}\right)={a}_{{p}} \:\left({x}^{{p}} \right)^{\left({p}\right)} ={a}_{{p}} {p}\left({p}−\mathrm{1}\right)....\mathrm{1}={p}!\:{a}_{{p}} \:\Rightarrow \\ $$$${a}_{{p}} =\frac{{p}^{\left({p}\right)} \left(\mathrm{0}\right)}{{p}!}\:. \\ $$
