
Previous in Relation and Functions Next in Relation and Functions
Question Number 65915 by mathmax by abdo last updated on 05/Aug/19
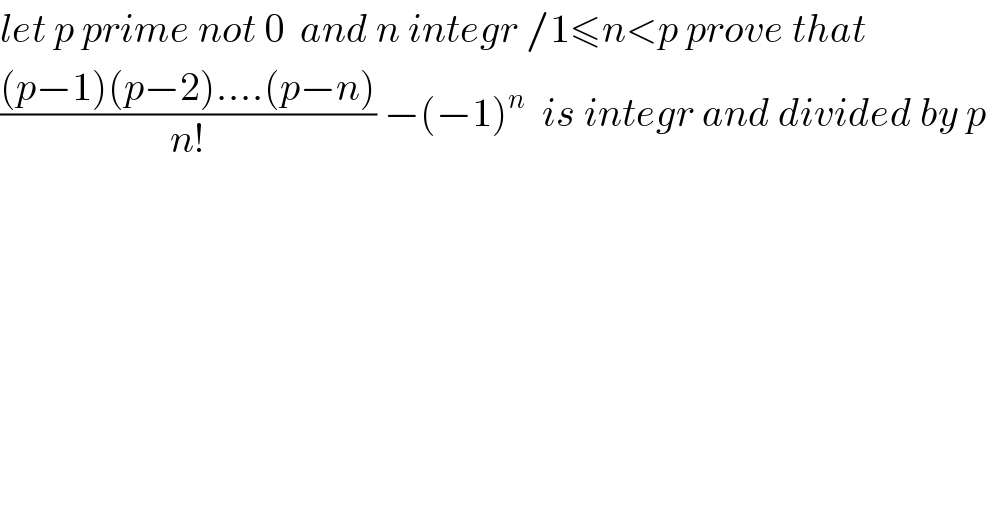
$${let}\:{p}\:{prime}\:{not}\:\mathrm{0}\:\:{and}\:{n}\:{integr}\:/\mathrm{1}\leqslant{n}<{p}\:{prove}\:{that} \\ $$$$\frac{\left({p}−\mathrm{1}\right)\left({p}−\mathrm{2}\right)....\left({p}−{n}\right)}{{n}!}\:−\left(−\mathrm{1}\right)^{{n}} \:\:{is}\:{integr}\:{and}\:{divided}\:{by}\:{p} \\ $$
