Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 194710 by York12 last updated on 14/Jul/23

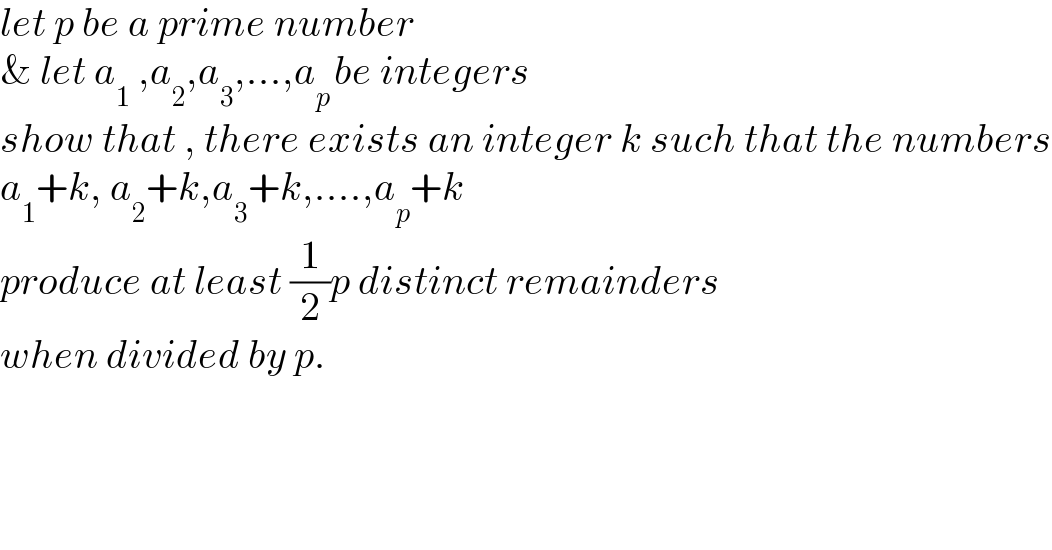
let p be a prime number & let a_1 ,a_2 ,a_3 ,...,a_(p ) be integers show that , there exists an integer k such that the numbers a_1 +k, a_2 +k,a_3 +k,....,a_p +k produce at least (1/2)p distinct remainders when divided by p.

$${let}\:{p}\:{be}\:{a}\:{prime}\:{number} \\ $$$$\&\:{let}\:{a}_{\mathrm{1}} \:,{a}_{\mathrm{2}} ,{a}_{\mathrm{3}} ,...,{a}_{{p}\:} {be}\:{integers} \\ $$$${show}\:{that}\:,\:{there}\:{exists}\:{an}\:{integer}\:{k}\:{such}\:{that}\:{the}\:{numbers} \\ $$$${a}_{\mathrm{1}} +{k},\:{a}_{\mathrm{2}} +{k},{a}_{\mathrm{3}} +{k},....,{a}_{{p}} +{k} \\ $$$${produce}\:{at}\:{least}\:\frac{\mathrm{1}}{\mathrm{2}}{p}\:{distinct}\:{remainders} \\ $$$${when}\:{divided}\:{by}\:{p}. \\ $$

Commented by Tinku Tara last updated on 14/Jul/23

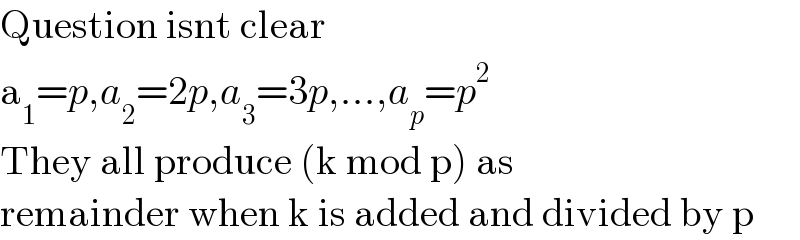
Question isnt clear a_1 =p,a_2 =2p,a_3 =3p,...,a_p =p^2 They all produce (k mod p) as remainder when k is added and divided by p

$$\mathrm{Question}\:\mathrm{isnt}\:\mathrm{clear} \\ $$$$\mathrm{a}_{\mathrm{1}} ={p},{a}_{\mathrm{2}} =\mathrm{2}{p},{a}_{\mathrm{3}} =\mathrm{3}{p},...,{a}_{{p}} ={p}^{\mathrm{2}} \\ $$$$\mathrm{They}\:\mathrm{all}\:\mathrm{produce}\:\left(\mathrm{k}\:\mathrm{mod}\:\mathrm{p}\right)\:\mathrm{as} \\ $$$$\mathrm{remainder}\:\mathrm{when}\:\mathrm{k}\:\mathrm{is}\:\mathrm{added}\:\mathrm{and}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{p} \\ $$

Commented by York12 last updated on 14/Jul/23

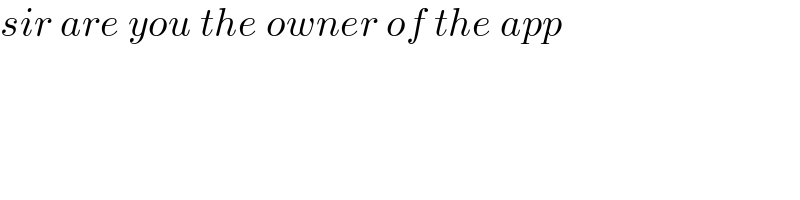
sir are you the owner of the app

$${sir}\:{are}\:{you}\:{the}\:{owner}\:{of}\:{the}\:{app} \\ $$

Commented by York12 last updated on 14/Jul/23

if so please work on converting into latex tool it produces wrong latax codes

$${if}\:{so}\:{please}\:{work}\:{on}\:{converting}\:{into}\: \\ $$$${latex}\:{tool} \\ $$$${it}\:{produces}\:{wrong}\:{latax}\:{codes} \\ $$$$ \\ $$

Commented by Tinku Tara last updated on 14/Jul/23

Type the equation that generated wrong latex as comment here and and we will check.

$$\mathrm{Type}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{that}\:\mathrm{generated} \\ $$$$\mathrm{wrong}\:\mathrm{latex}\:\mathrm{as}\:\mathrm{comment}\:\mathrm{here}\:\mathrm{and} \\ $$$$\mathrm{and}\:\mathrm{we}\:\mathrm{will}\:\mathrm{check}. \\ $$

Commented by York12 last updated on 14/Jul/23

okay sir thanks

$${okay}\:{sir}\:{thanks} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by Tinku Tara last updated on 14/Jul/23

You can visit Https://www.tinkutara.com. The web site has the same forum displayed as latex.

Commented by York12 last updated on 14/Jul/23

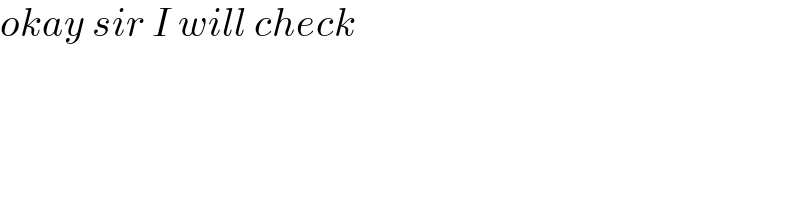
okay sir I will check

$${okay}\:{sir}\:{I}\:{will}\:{check} \\ $$

Commented by York12 last updated on 14/Jul/23

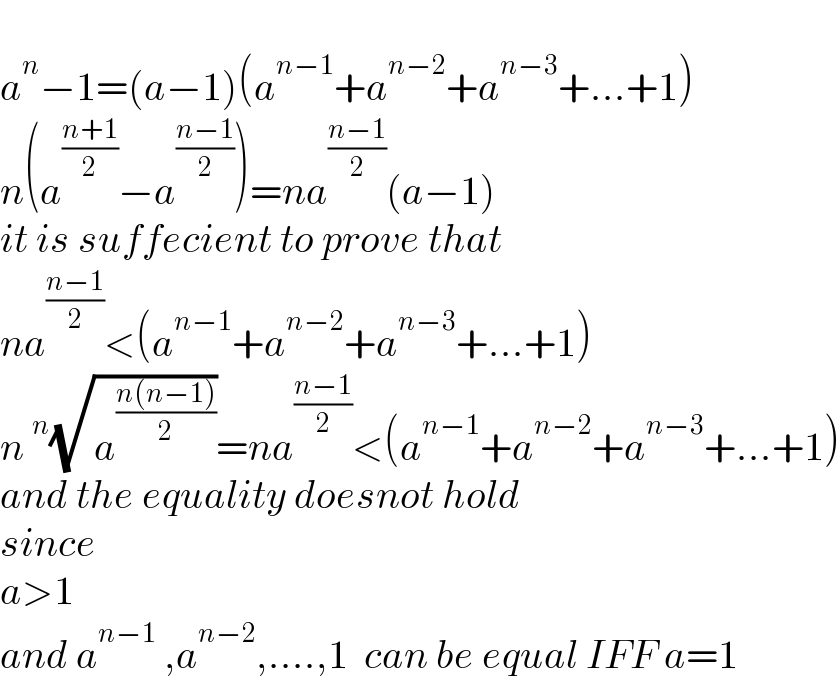
a^n −1=(a−1)(a^(n−1) +a^(n−2) +a^(n−3) +...+1) n(a^((n+1)/2) −a^((n−1)/2) )=na^((n−1)/2) (a−1) it is suffecient to prove that na^((n−1)/2) <(a^(n−1) +a^(n−2) +a^(n−3) +...+1) n^n (√a^((n(n−1))/2) )=na^((n−1)/2) <(a^(n−1) +a^(n−2) +a^(n−3) +...+1) and the equality doesnot hold since a>1 and a^(n−1) ,a^(n−2) ,....,1 can be equal IFF a=1

$$ \\ $$$${a}^{{n}} −\mathrm{1}=\left({a}−\mathrm{1}\right)\left({a}^{{n}−\mathrm{1}} +{a}^{{n}−\mathrm{2}} +{a}^{{n}−\mathrm{3}} +...+\mathrm{1}\right) \\ $$$${n}\left({a}^{\frac{{n}+\mathrm{1}}{\mathrm{2}}} −{a}^{\frac{{n}−\mathrm{1}}{\mathrm{2}}} \right)={na}^{\frac{{n}−\mathrm{1}}{\mathrm{2}}} \left({a}−\mathrm{1}\right) \\ $$$${it}\:{is}\:{suffecient}\:{to}\:{prove}\:{that} \\ $$$${na}^{\frac{{n}−\mathrm{1}}{\mathrm{2}}} <\left({a}^{{n}−\mathrm{1}} +{a}^{{n}−\mathrm{2}} +{a}^{{n}−\mathrm{3}} +...+\mathrm{1}\right) \\ $$$${n}\:^{{n}} \sqrt{{a}^{\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}} }={na}^{\frac{{n}−\mathrm{1}}{\mathrm{2}}} <\left({a}^{{n}−\mathrm{1}} +{a}^{{n}−\mathrm{2}} +{a}^{{n}−\mathrm{3}} +...+\mathrm{1}\right) \\ $$$${and}\:{the}\:{equality}\:{doesnot}\:{hold} \\ $$$${since} \\ $$$${a}>\mathrm{1} \\ $$$${and}\:{a}^{{n}−\mathrm{1}} \:,{a}^{{n}−\mathrm{2}} ,....,\mathrm{1}\:\:{can}\:{be}\:{equal}\:{IFF}\:{a}=\mathrm{1} \\ $$

Commented by York12 last updated on 14/Jul/23

u=Σ_(n=1) ^(2023) ⌊((n^2 −na)/5)⌋ , ⌊((n^2 −na)/5)⌋=((n^2 −na)/5)−{((n^2 −na)/5)} where {⊛} indicates the fractional part function 0≤{((n^2 −na)/5)}<1 ⇒ 0≤Σ_(n=1) ^(2023) {((n^2 −na)/5)}<2023 −1000<Σ_(n=1) ^(2023) ⌊((n^2 −na)/5)⌋<1000 ⇒ 0<Σ_(n=1) ^(2023) (((n^2 −na)/5))−Σ_(n=1) ^(2023) {((n^2 −na)/5)}<1000 ⇒−3023<Σ_(n=1) ^(2023) (((n^2 −na)/5))<1000 ⇒−3023<((Σ_(n=1) ^(2023) (n^2 ))/5)−((aΣ_(n=1) ^(2023) (n))/5)<1000 ⇒5×(3023+((Σ_(n=1) ^(2023) (n^2 ))/5))>a>5×(((Σ_(n=1) ^(2023) (n))/5)−1000) ⇒ 1349.007>a>1348.998 ⇒ a=1349 ∴u=Σ_(n=1) ^(2023) ⌊((n^2 −1349n)/5)⌋=Σ_(n=1) ^(2023) (((n^2 −1349n)/5))−Σ_(n=1) ^(2023) {((n^2 −1349n)/5)} Σ_(n=1) ^(2023) (((n^2 −1349n)/5))=0 ⇒ u=−Σ_(n=1) ^(2023) {((n^2 −1349n)/5)} so now we are only intrested in the value of the Remainder of the expression ((n^2 −1349n)/5) , one of the special properties of mod (5) & mod (10) that a_n a_(n−1) a_(n−2) a_(n−2) ...a_1 a_0 ≡ a_0 mod (5) a_n a_(n−1) a_(n−2) a_(n−2) ...a_1 a_0 ≡ a_0 mod(10) Σ_(n=1) ^(2023) {((n^2 −1349n)/5)}=⌊((2023)/5)⌋Σ_(n=1) ^5 ((((((n^2 −1349n)/5))mod(5))/5))+Σ_(n=1) ^(2023 mod(5)) ((((((n^2 −1349n)/5))mod(5))/5)) Σ_(n=1) ^5 ((((((n^2 −1349n)/5))mod(5))/5))=1 , Σ_(n=1) ^(2023 mod(5)) ((((((n^2 −1349n)/5))mod(5))/5))=1 ⇒u= −1×((404×1)+1)=−405 ⇒ u +a =944

$$ \\ $$$$ \\ $$$$ \\ $$$$\boldsymbol{{u}}=\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}\lfloor\frac{\boldsymbol{{n}}^{\mathrm{2}} −\boldsymbol{{na}}}{\mathrm{5}}\rfloor\:,\:\lfloor\frac{\boldsymbol{{n}}^{\mathrm{2}} −\boldsymbol{{na}}}{\mathrm{5}}\rfloor=\frac{\boldsymbol{{n}}^{\mathrm{2}} −\boldsymbol{{na}}}{\mathrm{5}}−\left\{\frac{\boldsymbol{{n}}^{\mathrm{2}} −\boldsymbol{{na}}}{\mathrm{5}}\right\} \\ $$$$\boldsymbol{{where}}\:\left\{\circledast\right\}\:\boldsymbol{{indicates}}\:\boldsymbol{{the}}\:\boldsymbol{{fractional}}\: \\ $$$$\boldsymbol{{part}}\:\boldsymbol{{function}}\: \\ $$$$\mathrm{0}\leqslant\left\{\frac{\boldsymbol{{n}}^{\mathrm{2}} −\boldsymbol{{na}}}{\mathrm{5}}\right\}<\mathrm{1}\:\Rightarrow\:\mathrm{0}\leqslant\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}\left\{\frac{\boldsymbol{{n}}^{\mathrm{2}} −\boldsymbol{{na}}}{\mathrm{5}}\right\}<\mathrm{2023} \\ $$$$−\mathrm{1000}<\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}\lfloor\frac{\boldsymbol{{n}}^{\mathrm{2}} −\boldsymbol{{na}}}{\mathrm{5}}\rfloor<\mathrm{1000}\:\Rightarrow\:\mathrm{0}<\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}\left(\frac{\boldsymbol{{n}}^{\mathrm{2}} −\boldsymbol{{na}}}{\mathrm{5}}\right)−\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}\left\{\frac{\boldsymbol{{n}}^{\mathrm{2}} −\boldsymbol{{na}}}{\mathrm{5}}\right\}<\mathrm{1000} \\ $$$$\Rightarrow−\mathrm{3023}<\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}\left(\frac{\boldsymbol{{n}}^{\mathrm{2}} −\boldsymbol{{na}}}{\mathrm{5}}\right)<\mathrm{1000} \\ $$$$\Rightarrow−\mathrm{3023}<\frac{\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}\left(\boldsymbol{{n}}^{\mathrm{2}} \right)}{\mathrm{5}}−\frac{\boldsymbol{{a}}\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}\left(\boldsymbol{{n}}\right)}{\mathrm{5}}<\mathrm{1000} \\ $$$$\Rightarrow\mathrm{5}×\left(\mathrm{3023}+\frac{\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}\left(\boldsymbol{{n}}^{\mathrm{2}} \right)}{\mathrm{5}}\right)>\boldsymbol{{a}}>\mathrm{5}×\left(\frac{\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}\left(\boldsymbol{{n}}\right)}{\mathrm{5}}−\mathrm{1000}\right) \\ $$$$\Rightarrow\:\mathrm{1349}.\mathrm{007}>{a}>\mathrm{1348}.\mathrm{998}\:\Rightarrow\:{a}=\mathrm{1349} \\ $$$$\therefore\boldsymbol{{u}}=\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}\lfloor\frac{\boldsymbol{{n}}^{\mathrm{2}} −\mathrm{1349}\boldsymbol{{n}}}{\mathrm{5}}\rfloor=\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}\left(\frac{\boldsymbol{{n}}^{\mathrm{2}} −\mathrm{1349}\boldsymbol{{n}}}{\mathrm{5}}\right)−\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}\left\{\frac{\boldsymbol{{n}}^{\mathrm{2}} −\mathrm{1349}\boldsymbol{{n}}}{\mathrm{5}}\right\} \\ $$$$\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}\left(\frac{\boldsymbol{{n}}^{\mathrm{2}} −\mathrm{1349}\boldsymbol{{n}}}{\mathrm{5}}\right)=\mathrm{0}\:\Rightarrow\:\boldsymbol{{u}}=−\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}\left\{\frac{\boldsymbol{{n}}^{\mathrm{2}} −\mathrm{1349}\boldsymbol{{n}}}{\mathrm{5}}\right\} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{now}}\:\boldsymbol{{we}}\:\boldsymbol{{are}}\:\boldsymbol{{only}}\:\boldsymbol{{intrested}}\:\boldsymbol{{in}}\:\boldsymbol{{the}}\:\boldsymbol{{value}} \\ $$$$\boldsymbol{{of}}\:\boldsymbol{{the}}\:\boldsymbol{{Remainder}}\:\boldsymbol{{of}}\:\boldsymbol{{the}}\:\boldsymbol{{expression}} \\ $$$$\frac{\boldsymbol{{n}}^{\mathrm{2}} −\mathrm{1349}\boldsymbol{{n}}}{\mathrm{5}}\:\:,\:\boldsymbol{{one}}\:\boldsymbol{{of}}\:\boldsymbol{{the}}\:\boldsymbol{{special}}\:\boldsymbol{{properties}} \\ $$$$\boldsymbol{{of}}\:\boldsymbol{{mod}}\:\left(\mathrm{5}\right)\:\&\:\boldsymbol{{mod}}\:\left(\mathrm{10}\right)\:\boldsymbol{{that}}\: \\ $$$$\boldsymbol{{a}}_{\boldsymbol{{n}}} \boldsymbol{{a}}_{\boldsymbol{{n}}−\mathrm{1}} \boldsymbol{{a}}_{\boldsymbol{{n}}−\mathrm{2}} \boldsymbol{{a}}_{\boldsymbol{{n}}−\mathrm{2}} ...\boldsymbol{{a}}_{\mathrm{1}} \boldsymbol{{a}}_{\mathrm{0}} \:\equiv\:\boldsymbol{{a}}_{\mathrm{0}} \:\boldsymbol{{mod}}\:\left(\mathrm{5}\right) \\ $$$$\boldsymbol{{a}}_{\boldsymbol{{n}}} \boldsymbol{{a}}_{\boldsymbol{{n}}−\mathrm{1}} \boldsymbol{{a}}_{\boldsymbol{{n}}−\mathrm{2}} \boldsymbol{{a}}_{\boldsymbol{{n}}−\mathrm{2}} ...\boldsymbol{{a}}_{\mathrm{1}} \boldsymbol{{a}}_{\mathrm{0}} \:\equiv\:\boldsymbol{{a}}_{\mathrm{0}} \:\boldsymbol{{mod}}\left(\mathrm{10}\right) \\ $$$$\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}\left\{\frac{\boldsymbol{{n}}^{\mathrm{2}} −\mathrm{1349}\boldsymbol{{n}}}{\mathrm{5}}\right\}=\lfloor\frac{\mathrm{2023}}{\mathrm{5}}\rfloor\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\mathrm{5}} {\sum}}\left(\frac{\left(\frac{\boldsymbol{{n}}^{\mathrm{2}} −\mathrm{1349}\boldsymbol{{n}}}{\mathrm{5}}\right)\boldsymbol{{mod}}\left(\mathrm{5}\right)}{\mathrm{5}}\right)+\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\mathrm{2023}\:\boldsymbol{{mod}}\left(\mathrm{5}\right)} {\sum}}\left(\frac{\left(\frac{\boldsymbol{{n}}^{\mathrm{2}} −\mathrm{1349}\boldsymbol{{n}}}{\mathrm{5}}\right)\boldsymbol{{mod}}\left(\mathrm{5}\right)}{\mathrm{5}}\right) \\ $$$$\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\mathrm{5}} {\sum}}\left(\frac{\left(\frac{\boldsymbol{{n}}^{\mathrm{2}} −\mathrm{1349}\boldsymbol{{n}}}{\mathrm{5}}\right)\boldsymbol{{mod}}\left(\mathrm{5}\right)}{\mathrm{5}}\right)=\mathrm{1}\:,\:\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\mathrm{2023}\:\boldsymbol{{mod}}\left(\mathrm{5}\right)} {\sum}}\left(\frac{\left(\frac{\boldsymbol{{n}}^{\mathrm{2}} −\mathrm{1349}\boldsymbol{{n}}}{\mathrm{5}}\right)\boldsymbol{{mod}}\left(\mathrm{5}\right)}{\mathrm{5}}\right)=\mathrm{1} \\ $$$$\Rightarrow\boldsymbol{{u}}=\:−\mathrm{1}×\left(\left(\mathrm{404}×\mathrm{1}\right)+\mathrm{1}\right)=−\mathrm{405} \\ $$$$\Rightarrow\:\boldsymbol{{u}}\:+\boldsymbol{{a}}\:=\mathrm{944}\: \\ $$

Commented by York12 last updated on 14/Jul/23

and I hope if you can add some codes for text colour

$${and}\:{I}\:{hope}\:{if}\:{you}\:{can}\:{add}\:{some}\:{codes}\:{for} \\ $$$${text}\:{colour} \\ $$

Commented by Tinku Tara last updated on 14/Jul/23

for the equation with a^n latex is correct tap on 3 dots → get latex paste latex in mathjax to validate

$$\mathrm{for}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{with}\:{a}^{{n}} \:\mathrm{latex}\:\mathrm{is}\:\mathrm{correct} \\ $$$$\mathrm{tap}\:\mathrm{on}\:\mathrm{3}\:\mathrm{dots}\:\rightarrow\:{get}\:{latex} \\ $$$${paste}\:{latex}\:{in}\:{mathjax}\:{to}\:{validate} \\ $$

Commented by York12 last updated on 14/Jul/23

I was using overleaf okay sir I will try

$${I}\:{was}\:{using}\:{overleaf} \\ $$$${okay}\:{sir}\:{I}\:{will}\:{try} \\ $$

Commented by Tinku Tara last updated on 14/Jul/23

https://www.mathjax.org/#demo

Commented by Tinku Tara last updated on 14/Jul/23

text color is additional latex module not supported in many places so colors are not coded

$$\mathrm{text}\:\mathrm{color}\:\mathrm{is}\:\mathrm{additional}\:\mathrm{latex}\:\mathrm{module}\:\mathrm{not} \\ $$$$\mathrm{supported}\:\mathrm{in}\:\mathrm{many}\:\mathrm{places}\:\mathrm{so}\:\mathrm{colors} \\ $$$$\mathrm{are}\:\mathrm{not}\:\mathrm{coded} \\ $$

Commented by York12 last updated on 14/Jul/23

okay sir thanks

$${okay}\:{sir}\:{thanks} \\ $$

Commented by York12 last updated on 18/Aug/23

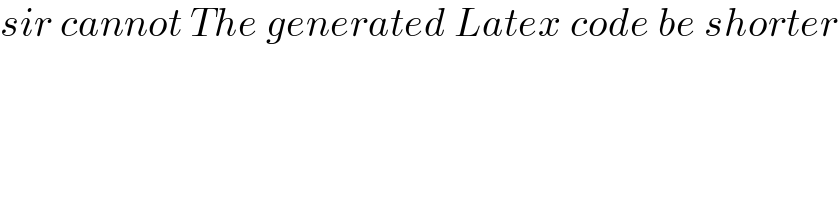
sir cannot The generated Latex code be shorter

$${sir}\:{cannot}\:{The}\:{generated}\:{Latex}\:{code}\:{be}\:{shorter} \\ $$

Commented by York12 last updated on 18/Aug/23

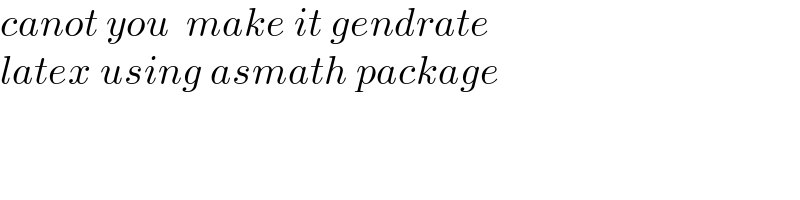
canot you make it gendrate latex using asmath package

$${canot}\:{you}\:\:{make}\:{it}\:{gendrate}\: \\ $$$${latex}\:{using}\:{asmath}\:{package} \\ $$

Commented by Tinku Tara last updated on 18/Aug/23

The generate could probably be shorter but you really need to make minor modification only Microsoft Equation Editor and MathJax are able to show this code without modification

$$\mathrm{The}\:\mathrm{generate}\:\mathrm{could}\:\mathrm{probably}\:\mathrm{be}\:\mathrm{shorter} \\ $$$$\mathrm{but}\:\mathrm{you}\:\mathrm{really}\:\mathrm{need}\:\mathrm{to}\:\mathrm{make}\:\mathrm{minor}\:\mathrm{modification} \\ $$$$\mathrm{only} \\ $$$$\mathrm{Microsoft}\:\mathrm{Equation}\:\mathrm{Editor}\:\mathrm{and}\:\mathrm{MathJax} \\ $$$$\mathrm{are}\:\mathrm{able}\:\mathrm{to}\:\mathrm{show}\:\mathrm{this}\:\mathrm{code}\:\mathrm{without} \\ $$$$\mathrm{modification} \\ $$

Commented by York12 last updated on 18/Aug/23

thanks

$${thanks} \\ $$

Commented by Tinku Tara last updated on 18/Aug/23

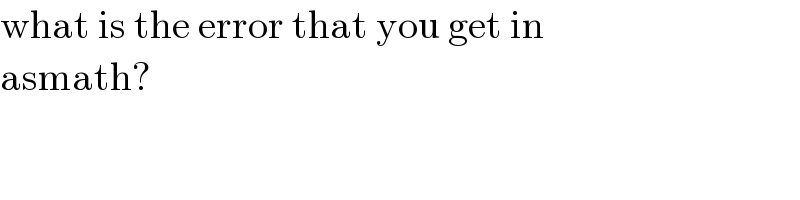
what is the error that you get in asmath?

$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{error}\:\mathrm{that}\:\mathrm{you}\:\mathrm{get}\:\mathrm{in} \\ $$$$\mathrm{asmath}? \\ $$

Commented by York12 last updated on 18/Aug/23

Ovearleaf was giving alerts for errors but it is okay now

$${Ovearleaf}\:{was}\:{giving}\:{alerts}\:{for}\:{errors} \\ $$$${but}\:{it}\:{is}\:{okay}\:{now} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com