
Question Number 29461 by prof Abdo imad last updated on 09/Feb/18
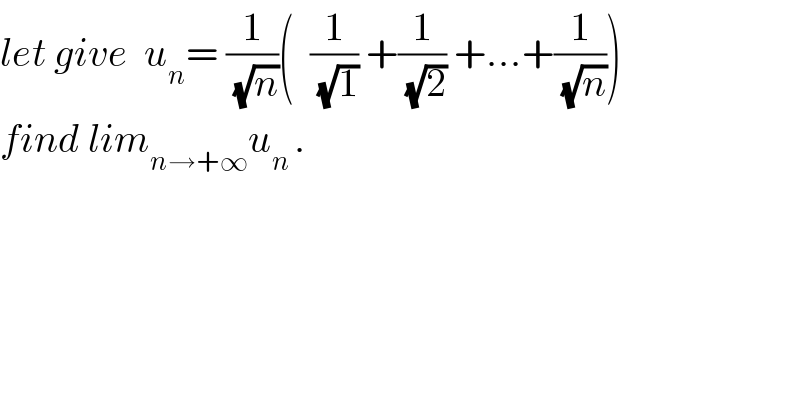
$${let}\:{give}\:\:{u}_{{n}} =\:\frac{\mathrm{1}}{\sqrt{{n}}}\left(\:\:\frac{\mathrm{1}}{\sqrt{\mathrm{1}}}\:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:+...+\frac{\mathrm{1}}{\sqrt{{n}}}\right)\: \\ $$$${find}\:{lim}_{{n}\rightarrow+\infty} {u}_{{n}\:} . \\ $$
Commented by prof Abdo imad last updated on 13/Feb/18
![we have u_n =((√n)/n)( (1/(√1)) + (1/(√2)) +.....+(1/(√n))) = (1/n)( (1/(√(1/n))) +(1/(√(2/n))) +....+(1/(√(n/n)))) = (1/n)Σ_(k=1) ^n (1/(√(k/n))) so u_(n ) is a Rieman sum and lim_(n→∞) u_n = ∫_0 ^1 (dx/(√x)) =[2(√(x ))]_0 ^1 = 2 .](Q29861.png)
$${we}\:{have}\:{u}_{{n}} =\frac{\sqrt{{n}}}{{n}}\left(\:\:\frac{\mathrm{1}}{\sqrt{\mathrm{1}}}\:+\:\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:+.....+\frac{\mathrm{1}}{\sqrt{{n}}}\right) \\ $$$$=\:\frac{\mathrm{1}}{{n}}\left(\:\:\frac{\mathrm{1}}{\sqrt{\frac{\mathrm{1}}{{n}}}}\:+\frac{\mathrm{1}}{\sqrt{\frac{\mathrm{2}}{{n}}}}\:+....+\frac{\mathrm{1}}{\sqrt{\frac{{n}}{{n}}}}\right) \\ $$$$=\:\frac{\mathrm{1}}{{n}}\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{\sqrt{\frac{{k}}{{n}}}}\:{so}\:{u}_{{n}\:} \:{is}\:{a}\:{Rieman}\:{sum}\:{and} \\ $$$${lim}_{{n}\rightarrow\infty} \:{u}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dx}}{\sqrt{{x}}}\:\:=\left[\mathrm{2}\sqrt{{x}\:}\right]_{\mathrm{0}} ^{\mathrm{1}} =\:\mathrm{2}\:. \\ $$
