
Question Number 31747 by abdo imad last updated on 13/Mar/18
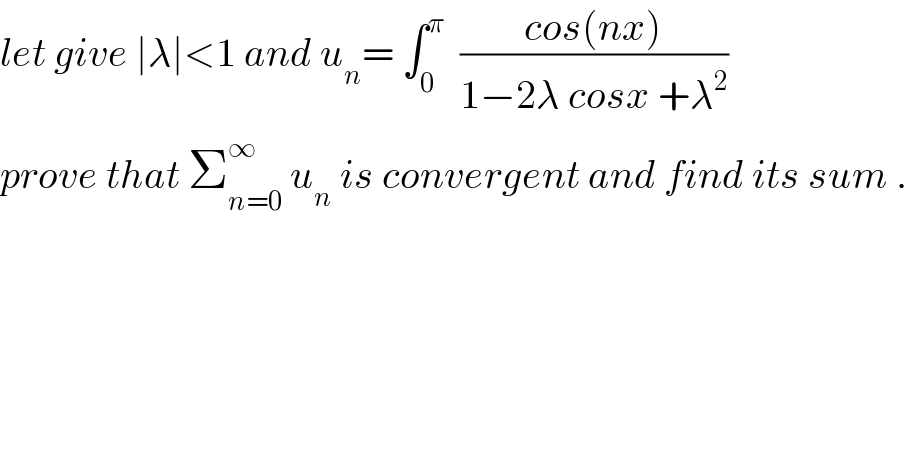
$${let}\:{give}\:\mid\lambda\mid<\mathrm{1}\:{and}\:{u}_{{n}} =\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{cos}\left({nx}\right)}{\mathrm{1}−\mathrm{2}\lambda\:{cosx}\:+\lambda^{\mathrm{2}} } \\ $$$${prove}\:{that}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{u}_{{n}} \:{is}\:{convergent}\:{and}\:{find}\:{its}\:{sum}\:. \\ $$
Commented by abdo imad last updated on 14/Mar/18
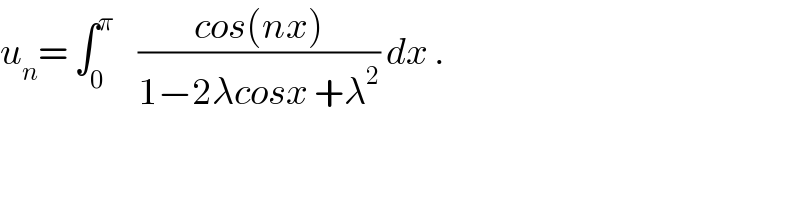
$${u}_{{n}} =\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\frac{{cos}\left({nx}\right)}{\mathrm{1}−\mathrm{2}\lambda{cosx}\:+\lambda^{\mathrm{2}} }\:{dx}\:. \\ $$
