Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 195571 by York12 last updated on 05/Aug/23

let f(x+y)+f(x−y)=2f(x)f(y)∧f((1/2))=−1 compute Σ_(k=1) ^(20) [(1/(sin (k)sin (k+f(k))))]

$${let}\:{f}\left({x}+{y}\right)+{f}\left({x}−{y}\right)=\mathrm{2}{f}\left({x}\right){f}\left({y}\right)\wedge{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−\mathrm{1} \\ $$$${compute}\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{20}} {\sum}}\left[\frac{\mathrm{1}}{\mathrm{sin}\:\left({k}\right)\mathrm{sin}\:\left({k}+{f}\left({k}\right)\right)}\right] \\ $$

Answered by mahdipoor last updated on 05/Aug/23

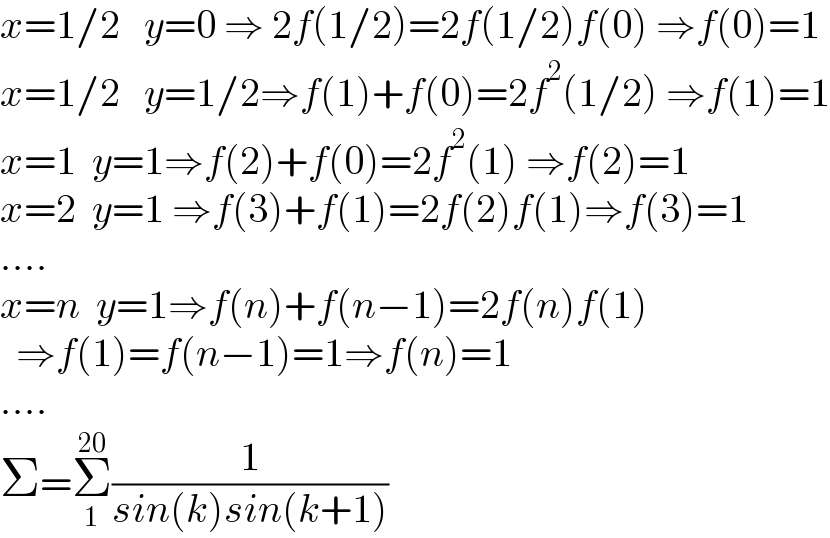
x=1/2 y=0 ⇒ 2f(1/2)=2f(1/2)f(0) ⇒f(0)=1 x=1/2 y=1/2⇒f(1)+f(0)=2f^2 (1/2) ⇒f(1)=1 x=1 y=1⇒f(2)+f(0)=2f^2 (1) ⇒f(2)=1 x=2 y=1 ⇒f(3)+f(1)=2f(2)f(1)⇒f(3)=1 .... x=n y=1⇒f(n)+f(n−1)=2f(n)f(1) ⇒f(1)=f(n−1)=1⇒f(n)=1 .... Σ=Σ_1 ^(20) (1/(sin(k)sin(k+1)))

$${x}=\mathrm{1}/\mathrm{2}\:\:\:{y}=\mathrm{0}\:\Rightarrow\:\mathrm{2}{f}\left(\mathrm{1}/\mathrm{2}\right)=\mathrm{2}{f}\left(\mathrm{1}/\mathrm{2}\right){f}\left(\mathrm{0}\right)\:\Rightarrow{f}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$${x}=\mathrm{1}/\mathrm{2}\:\:\:{y}=\mathrm{1}/\mathrm{2}\Rightarrow{f}\left(\mathrm{1}\right)+{f}\left(\mathrm{0}\right)=\mathrm{2}{f}^{\mathrm{2}} \left(\mathrm{1}/\mathrm{2}\right)\:\Rightarrow{f}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$${x}=\mathrm{1}\:\:{y}=\mathrm{1}\Rightarrow{f}\left(\mathrm{2}\right)+{f}\left(\mathrm{0}\right)=\mathrm{2}{f}^{\mathrm{2}} \left(\mathrm{1}\right)\:\Rightarrow{f}\left(\mathrm{2}\right)=\mathrm{1} \\ $$$${x}=\mathrm{2}\:\:{y}=\mathrm{1}\:\Rightarrow{f}\left(\mathrm{3}\right)+{f}\left(\mathrm{1}\right)=\mathrm{2}{f}\left(\mathrm{2}\right){f}\left(\mathrm{1}\right)\Rightarrow{f}\left(\mathrm{3}\right)=\mathrm{1} \\ $$$$.... \\ $$$${x}={n}\:\:{y}=\mathrm{1}\Rightarrow{f}\left({n}\right)+{f}\left({n}−\mathrm{1}\right)=\mathrm{2}{f}\left({n}\right){f}\left(\mathrm{1}\right) \\ $$$$\:\:\Rightarrow{f}\left(\mathrm{1}\right)={f}\left({n}−\mathrm{1}\right)=\mathrm{1}\Rightarrow{f}\left({n}\right)=\mathrm{1} \\ $$$$.... \\ $$$$\Sigma=\underset{\mathrm{1}} {\overset{\mathrm{20}} {\sum}}\frac{\mathrm{1}}{{sin}\left({k}\right){sin}\left({k}+\mathrm{1}\right)} \\ $$

Answered by mr W last updated on 05/Aug/23

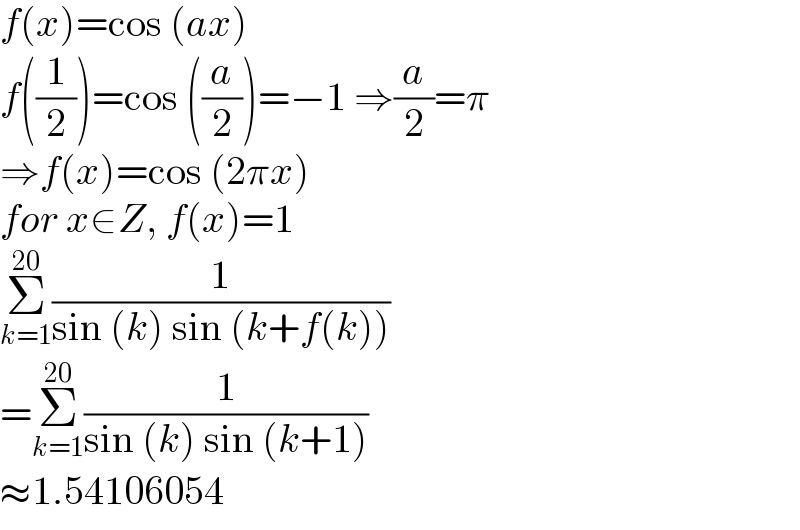
f(x)=cos (ax) f((1/2))=cos ((a/2))=−1 ⇒(a/2)=π ⇒f(x)=cos (2πx) for x∈Z, f(x)=1 Σ_(k=1) ^(20) (1/(sin (k) sin (k+f(k)))) =Σ_(k=1) ^(20) (1/(sin (k) sin (k+1))) ≈1.54106054

$${f}\left({x}\right)=\mathrm{cos}\:\left({ax}\right) \\ $$$${f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{cos}\:\left(\frac{{a}}{\mathrm{2}}\right)=−\mathrm{1}\:\Rightarrow\frac{{a}}{\mathrm{2}}=\pi \\ $$$$\Rightarrow{f}\left({x}\right)=\mathrm{cos}\:\left(\mathrm{2}\pi{x}\right) \\ $$$${for}\:{x}\in{Z},\:{f}\left({x}\right)=\mathrm{1} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{20}} {\sum}}\frac{\mathrm{1}}{\mathrm{sin}\:\left({k}\right)\:\mathrm{sin}\:\left({k}+{f}\left({k}\right)\right)} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{\mathrm{20}} {\sum}}\frac{\mathrm{1}}{\mathrm{sin}\:\left({k}\right)\:\mathrm{sin}\:\left({k}+\mathrm{1}\right)} \\ $$$$\approx\mathrm{1}.\mathrm{54106054} \\ $$

Commented by York12 last updated on 05/Aug/23

⇒f(x)=cos(2πx) ⇒Σ_(k=1) ^(20) [(1/(sin (k)sin (k+f(k))))]=Σ_(k=1) ^(20) [(1/(sin(k)sin(k+1)))] =cosec(1)Σ_(k=1) ^(20) [((sin(1))/(sin(k)sin(k+1)))]=cosec(1)Σ_(k=1) ^(20) [((sin(k+1−k))/(sin(k)sin(k+1)))] =cosec(1)Σ_(k=1) ^(20) [((sin(k+1)cos(k)−cos(k+1)sin(k))/(sin(k)sin(k+1)))] =cosec(1)Σ_(k=1) ^(20) [cot(k)−cot(k+1)] =cosec(1)[cot(1)−cot(21)]≈3133.3715

$$ \\ $$$$\Rightarrow{f}\left({x}\right)={cos}\left(\mathrm{2}\pi{x}\right) \\ $$$$\Rightarrow\underset{{k}=\mathrm{1}} {\overset{\mathrm{20}} {\sum}}\left[\frac{\mathrm{1}}{\mathrm{sin}\:\left({k}\right)\mathrm{sin}\:\left({k}+{f}\left({k}\right)\right)}\right]=\underset{{k}=\mathrm{1}} {\overset{\mathrm{20}} {\sum}}\left[\frac{\mathrm{1}}{{sin}\left({k}\right){sin}\left({k}+\mathrm{1}\right)}\right] \\ $$$$={cosec}\left(\mathrm{1}\right)\underset{{k}=\mathrm{1}} {\overset{\mathrm{20}} {\sum}}\left[\frac{{sin}\left(\mathrm{1}\right)}{{sin}\left({k}\right){sin}\left({k}+\mathrm{1}\right)}\right]={cosec}\left(\mathrm{1}\right)\underset{{k}=\mathrm{1}} {\overset{\mathrm{20}} {\sum}}\left[\frac{{sin}\left({k}+\mathrm{1}−{k}\right)}{{sin}\left({k}\right){sin}\left({k}+\mathrm{1}\right)}\right] \\ $$$$={cosec}\left(\mathrm{1}\right)\underset{{k}=\mathrm{1}} {\overset{\mathrm{20}} {\sum}}\left[\frac{{sin}\left({k}+\mathrm{1}\right){cos}\left({k}\right)−{cos}\left({k}+\mathrm{1}\right){sin}\left({k}\right)}{{sin}\left({k}\right){sin}\left({k}+\mathrm{1}\right)}\right] \\ $$$$={cosec}\left(\mathrm{1}\right)\underset{{k}=\mathrm{1}} {\overset{\mathrm{20}} {\sum}}\left[{cot}\left({k}\right)−{cot}\left({k}+\mathrm{1}\right)\right] \\ $$$$={cosec}\left(\mathrm{1}\right)\left[{cot}\left(\mathrm{1}\right)−{cot}\left(\mathrm{21}\right)\right]\approx\mathrm{3133}.\mathrm{3715} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com