
Question Number 93898 by mathmax by abdo last updated on 16/May/20
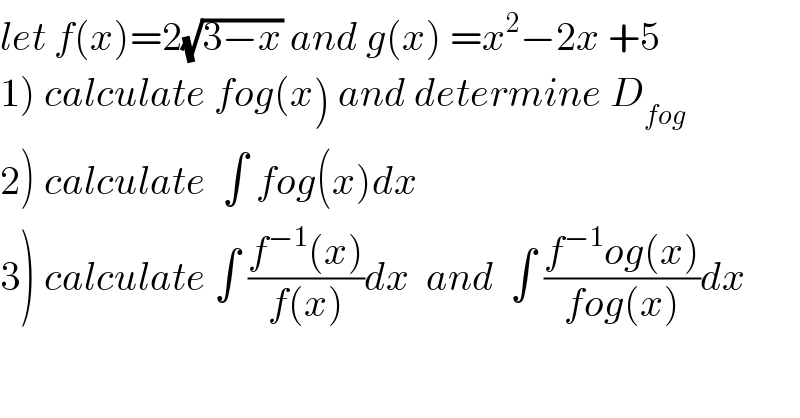
$${let}\:{f}\left({x}\right)=\mathrm{2}\sqrt{\mathrm{3}−{x}}\:{and}\:{g}\left({x}\right)\:={x}^{\mathrm{2}} −\mathrm{2}{x}\:+\mathrm{5} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{fog}\left({x}\right)\:{and}\:{determine}\:{D}_{{fog}} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\:\int\:{fog}\left({x}\right){dx} \\ $$$$\left.\mathrm{3}\right)\:{calculate}\:\int\:\frac{{f}^{−\mathrm{1}} \left({x}\right)}{{f}\left({x}\right)}{dx}\:\:{and}\:\:\int\:\frac{{f}^{−\mathrm{1}} {og}\left({x}\right)}{{fog}\left({x}\right)}{dx} \\ $$
Commented by mathmax by abdo last updated on 17/May/20
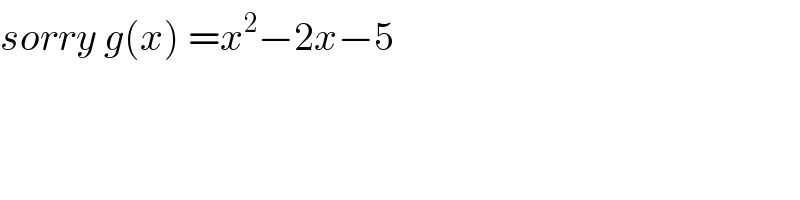
$${sorry}\:{g}\left({x}\right)\:={x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{5} \\ $$
Answered by Kunal12588 last updated on 16/May/20
![1⟩ fog(x)=2(√(3−x^2 +2x−5))=2(√(2x−x^2 −2)) what is meant by D_(fog) ?(derivative?) 2⟩ 2∫(√(−[(x−1)^2 +2−1])) dx =2∫(√(−(x−1)^2 −1)) dx it is like finding ∫(√(−x)) dx; I hvn′t learnt about complex integrals. 3⟩ f^(−1) (x)=3−(x^2 /2)=(1/2)(12−x^2 ) I=(1/4)∫((12−x^2 )/(√(3−x)))dx (√(3−x))=t⇒ x=3−t^2 ⇒ dx=−2t dt I=(1/4)∫((12−(3−t^2 )^2 )/t)(−2t)dt =(1/2)∫[(t^2 −3)^2 −12] dt=(1/2)∫(t^4 −6t^2 −3)dt =(1/(10))(3−x)^2 (√(3−x))−(3−x)(√(3−x))−(3/2)(√(3−x))+C =(1/(10))(x^2 −5x−9)(√(3−x))+C 4⟩ complex integral](Q93980.png)
$$\mathrm{1}\rangle\:{fog}\left({x}\right)=\mathrm{2}\sqrt{\mathrm{3}−{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{5}}=\mathrm{2}\sqrt{\mathrm{2}{x}−{x}^{\mathrm{2}} −\mathrm{2}} \\ $$$${what}\:{is}\:{meant}\:{by}\:{D}_{{fog}} ?\left({derivative}?\right) \\ $$$$\mathrm{2}\rangle\:\mathrm{2}\int\sqrt{−\left[\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}−\mathrm{1}\right]}\:{dx} \\ $$$$\:\:\:\:\:=\mathrm{2}\int\sqrt{−\left({x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}\:{dx} \\ $$$${it}\:{is}\:{like}\:{finding}\:\int\sqrt{−{x}}\:{dx};\:{I}\:{hvn}'{t}\:{learnt} \\ $$$${about}\:{complex}\:{integrals}. \\ $$$$\mathrm{3}\rangle\:{f}^{−\mathrm{1}} \left({x}\right)=\mathrm{3}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{12}−{x}^{\mathrm{2}} \right) \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{12}−{x}^{\mathrm{2}} }{\sqrt{\mathrm{3}−{x}}}{dx} \\ $$$$\:\:\:\:\:\sqrt{\mathrm{3}−{x}}={t}\Rightarrow\:{x}=\mathrm{3}−{t}^{\mathrm{2}} \Rightarrow\:{dx}=−\mathrm{2}{t}\:{dt} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{12}−\left(\mathrm{3}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{{t}}\left(−\mathrm{2}{t}\right){dt} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int\left[\left({t}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{2}} −\mathrm{12}\right]\:{dt}=\frac{\mathrm{1}}{\mathrm{2}}\int\left({t}^{\mathrm{4}} −\mathrm{6}{t}^{\mathrm{2}} −\mathrm{3}\right){dt} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{3}−{x}\right)^{\mathrm{2}} \sqrt{\mathrm{3}−{x}}−\left(\mathrm{3}−{x}\right)\sqrt{\mathrm{3}−{x}}−\frac{\mathrm{3}}{\mathrm{2}}\sqrt{\mathrm{3}−{x}}+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}\left({x}^{\mathrm{2}} −\mathrm{5}{x}−\mathrm{9}\right)\sqrt{\mathrm{3}−{x}}+{C} \\ $$$$\mathrm{4}\rangle\:{complex}\:{integral} \\ $$
Commented by mathmax by abdo last updated on 17/May/20

$${thank}\:{you}\:{kunal} \\ $$
Commented by mathmax by abdo last updated on 17/May/20

$${D}_{{fog}} \:{mean}\:{set}\:{of}\:{definition}..! \\ $$
