Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 64873 by mathmax by abdo last updated on 22/Jul/19

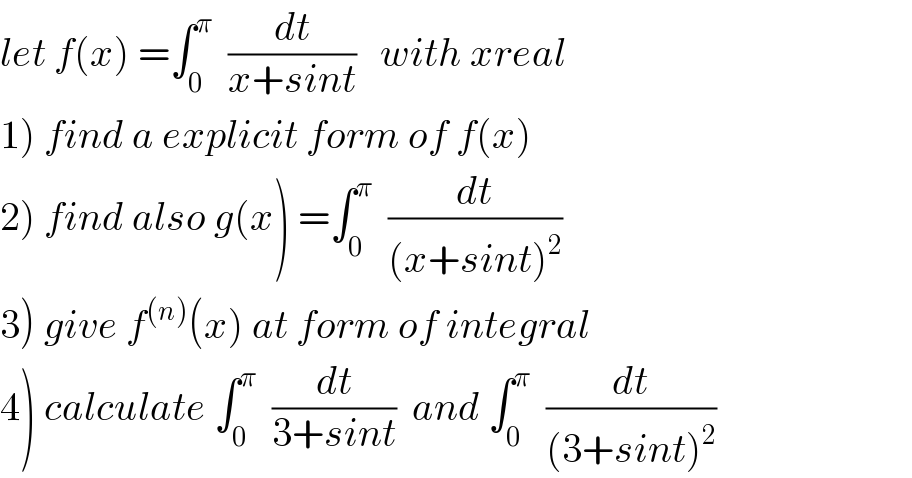
let f(x) =∫_0 ^π (dt/(x+sint)) with xreal 1) find a explicit form of f(x) 2) find also g(x) =∫_0 ^π (dt/((x+sint)^2 )) 3) give f^((n)) (x) at form of integral 4) calculate ∫_0 ^π (dt/(3+sint)) and ∫_0 ^π (dt/((3+sint)^2 ))

$${let}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\pi} \:\:\frac{{dt}}{{x}+{sint}}\:\:\:{with}\:{xreal} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:{also}\:{g}\left({x}\right)\:=\int_{\mathrm{0}} ^{\pi} \:\:\frac{{dt}}{\left({x}+{sint}\right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{3}\right)\:{give}\:{f}^{\left({n}\right)} \left({x}\right)\:{at}\:{form}\:{of}\:{integral} \\ $$$$\left.\mathrm{4}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{dt}}{\mathrm{3}+{sint}}\:\:{and}\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{dt}}{\left(\mathrm{3}+{sint}\right)^{\mathrm{2}} } \\ $$

Commented by mathmax by abdo last updated on 23/Jul/19

1)f(x) =∫_0 ^π (dt/(x+sint)) changement tan((t/2))=u give f(x) =∫_0 ^∞ (1/(x+((2u)/(1+u^2 )))) ((2du)/(1+u^2 )) =∫_0 ^∞ ((2du)/(x+xu^2 +2u)) =∫_0 ^∞ ((2du)/(xu^2 +2u +x)) xu^2 +2u +x =0→Δ^′ =1−x^2 case 1 1−x^2 >0 ⇒∣x∣<1 ⇒u_1 =((−1+(√(1−x^2 )))/x) and u_2 =((−1−(√(1−x^2 )))/x) ( x≠0) ⇒f(x) =∫_0 ^∞ ((2du)/(x(u−u_1 )(u−u_2 ))) =(2/x)(1/((2(√(1−x^2 )))/x))∫_0 ^∞ ((1/(u−u_1 ))−(1/(u−u_2 )))du =(1/(√(1−x^2 )))[ln∣((u−u_1 )/(u−u_2 ))∣]_0 ^(+∞) =(1/(√(1−x^2 ))){−ln(∣(u_1 /u_2 )∣)} =(1/(√(1−x^2 )))ln∣((1+(√(1−x^2 )))/(1−(√(1−x^2 ))))∣ case 2 1−x^2 <0 ⇒∣x∣>1 ⇒xu^2 +2u +x =x(u^2 +((2u)/x) +1) =x{ u^2 +2(u/x) +(1/x^2 ) +1−(1/x^2 )} =x{ (u+(1/x))^2 +((x^2 −1)/x^2 )} we use the changement u+(1/x) =((√(x^2 −1))/(∣x∣)) u ⇒ f(x) = ∫_0 ^∞ ((2du)/(x{(u+(1/x))^(2 ) +((x^2 −1)/x^2 )})) =(2/x)∫_0 ^∞ (1/(((x^2 −1)/x^2 )(1+u^2 )))((√(x^2 −1))/(∣x∣)) du =((2x^2 )/(x∣x∣)) ((√(x^2 −1))/(x^2 −1)) ∫_0 ^∞ (du/(1+u^2 )) =2ξ(x)(1/(√(x^2 −1))) (π/2) =((πξ(x))/(√(x^2 −1))) with ξ(x) =1 if x>0 and ξ(x)=−1 if x<0 x =0 ⇒f(x)=∫_0 ^π (dt/(sint)) =_(tan((t/2))=u) ∫_0 ^∞ (1/((2u)/(1+u^2 ))) ((2du)/(1+u^2 )) =∫_0 ^∞ (du/u) f(x)dont exist (the integral diverges!)

$$\left.\mathrm{1}\right){f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\pi} \:\frac{{dt}}{{x}+{sint}}\:\:{changement}\:{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}\:{give} \\ $$$${f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{{x}+\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2}{du}}{{x}+{xu}^{\mathrm{2}} \:+\mathrm{2}{u}}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{du}}{{xu}^{\mathrm{2}} \:+\mathrm{2}{u}\:+{x}} \\ $$$${xu}^{\mathrm{2}} \:+\mathrm{2}{u}\:+{x}\:=\mathrm{0}\rightarrow\Delta^{'} \:=\mathrm{1}−{x}^{\mathrm{2}} \\ $$$${case}\:\mathrm{1}\:\:\mathrm{1}−{x}^{\mathrm{2}} >\mathrm{0}\:\Rightarrow\mid{x}\mid<\mathrm{1}\:\Rightarrow{u}_{\mathrm{1}} =\frac{−\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}\:\:{and}\:{u}_{\mathrm{2}} =\frac{−\mathrm{1}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}} \\ $$$$\left(\:{x}\neq\mathrm{0}\right)\:\Rightarrow{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{du}}{{x}\left({u}−{u}_{\mathrm{1}} \right)\left({u}−{u}_{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{2}}{{x}}\frac{\mathrm{1}}{\frac{\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}}\int_{\mathrm{0}} ^{\infty} \:\left(\frac{\mathrm{1}}{{u}−{u}_{\mathrm{1}} }−\frac{\mathrm{1}}{{u}−{u}_{\mathrm{2}} }\right){du}\:=\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\left[{ln}\mid\frac{{u}−{u}_{\mathrm{1}} }{{u}−{u}_{\mathrm{2}} }\mid\right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\left\{−{ln}\left(\mid\frac{{u}_{\mathrm{1}} }{{u}_{\mathrm{2}} }\mid\right)\right\}\:=\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{ln}\mid\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\mathrm{1}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\mid \\ $$$${case}\:\mathrm{2}\:\:\mathrm{1}−{x}^{\mathrm{2}} <\mathrm{0}\:\Rightarrow\mid{x}\mid>\mathrm{1}\:\:\Rightarrow{xu}^{\mathrm{2}} \:+\mathrm{2}{u}\:+{x}\:={x}\left({u}^{\mathrm{2}} \:+\frac{\mathrm{2}{u}}{{x}}\:+\mathrm{1}\right) \\ $$$$={x}\left\{\:{u}^{\mathrm{2}} \:+\mathrm{2}\frac{{u}}{{x}}\:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right\}\:={x}\left\{\:\left({u}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} \:+\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} }\right\}\:{we}\:{use}\:{the} \\ $$$${changement}\:{u}+\frac{\mathrm{1}}{{x}}\:=\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{\mid{x}\mid}\:{u}\:\Rightarrow \\ $$$${f}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2}{du}}{{x}\left\{\left({u}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}\:} \:+\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} }\right\}}\:=\frac{\mathrm{2}}{{x}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} }\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{\mid{x}\mid}\:{du} \\ $$$$=\frac{\mathrm{2}{x}^{\mathrm{2}} }{{x}\mid{x}\mid}\:\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}^{\mathrm{2}} −\mathrm{1}}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\mathrm{2}\xi\left({x}\right)\frac{\mathrm{1}}{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:\frac{\pi}{\mathrm{2}}\:=\frac{\pi\xi\left({x}\right)}{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:{with} \\ $$$$\xi\left({x}\right)\:=\mathrm{1}\:{if}\:{x}>\mathrm{0}\:\:{and}\:\xi\left({x}\right)=−\mathrm{1}\:{if}\:{x}<\mathrm{0} \\ $$$${x}\:=\mathrm{0}\:\Rightarrow{f}\left({x}\right)=\int_{\mathrm{0}} ^{\pi} \:\frac{{dt}}{{sint}}\:=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\infty} \frac{{du}}{{u}} \\ $$$${f}\left({x}\right){dont}\:{exist}\:\left({the}\:{integral}\:{diverges}!\right) \\ $$

Commented by mathmax by abdo last updated on 23/Jul/19

2) we have f^′ (x) =−∫_0 ^π (dt/((x +sint)^2 )) =−g(x) ⇒g(x)=−f^′ (x) if ∣x∣>1 f(x) =((πξ(x))/(√(x^2 −1))) ⇒f^′ (x) =πξ(x){(x^2 −1)^(−(1/2)) }^((1)) =πξ(x)(−(1/2))(2x)(x^2 −1)^(−(3/2)) =−((πxξ(x))/((x^2 −1)(√(x^2 −1)))) ⇒ g(x) =((πxξ(x))/((x^2 −1)(√(x^2 −1)))) if ∣x∣<1 (x≠0) f(x)=(1/(√(1−x^2 )))ln∣((1+(√(1−x^2 )))/(1−(√(1−x^2 ))))∣ ⇒ f^′ (x)={(1−x^2 )^(−(1/2)) }^((1)) ln∣((1+(√(1−x^2 )))/(1−(√(1−x^2 ))))∣+(1/(√(1−x^2 ))) ((w^′ (x))/(w(x))) with w(x) =((1+(√(1−x^2 )))/(1−(√(1−x^2 )))) ⇒w^′ (x) =((((−2x)/(2(√(1−x^2 ))))(1−(√(1−x^2 )))−((x/(√(1−x^2 ))))(1+(√(1−x^2 ))))/((1−(√(1−x^2 )))^2 )) =((−(x/(√(1−x^2 ))) +x −(x/(√(1−x^2 )))−x)/((1−(√(1−x^2 )))^2 )) =((−2x)/((√(1−x^2 ))(1−(√(1−x^2 ))))) ⇒ f^′ (x) =(x/((1−x^2 )(√(1−x^2 ))))ln∣((1+(√(1−x^2 )))/(1−(√(1−x^2 ))))∣+(1/(√(1−x^2 ))) ((−2x)/((√(1−x^2 ))(1−(√(1−x^2 )))))×((1−(√(1−x^2 )))/(1+(√(1−x^2 )))) =....

$$\left.\mathrm{2}\right)\:{we}\:{have}\:{f}^{'} \left({x}\right)\:=−\int_{\mathrm{0}} ^{\pi} \:\:\frac{{dt}}{\left({x}\:+{sint}\right)^{\mathrm{2}} }\:=−{g}\left({x}\right)\:\Rightarrow{g}\left({x}\right)=−{f}^{'} \left({x}\right) \\ $$$${if}\:\:\mid{x}\mid>\mathrm{1}\:\:{f}\left({x}\right)\:=\frac{\pi\xi\left({x}\right)}{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:\Rightarrow{f}^{'} \left({x}\right)\:=\pi\xi\left({x}\right)\left\{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right\}^{\left(\mathrm{1}\right)} \\ $$$$=\pi\xi\left({x}\right)\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{2}{x}\right)\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:=−\frac{\pi{x}\xi\left({x}\right)}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:\Rightarrow \\ $$$${g}\left({x}\right)\:=\frac{\pi{x}\xi\left({x}\right)}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}} \\ $$$${if}\:\mid{x}\mid<\mathrm{1}\:\:\:\left({x}\neq\mathrm{0}\right)\:\:{f}\left({x}\right)=\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{ln}\mid\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\mathrm{1}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\mid\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)=\left\{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right\}^{\left(\mathrm{1}\right)} {ln}\mid\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\mathrm{1}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\mid+\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\frac{{w}^{'} \left({x}\right)}{{w}\left({x}\right)} \\ $$$${with}\:{w}\left({x}\right)\:=\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\mathrm{1}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\Rightarrow{w}^{'} \left({x}\right)\:=\frac{\frac{−\mathrm{2}{x}}{\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\left(\mathrm{1}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)−\left(\frac{{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\right)\left(\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)}{\left(\mathrm{1}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)^{\mathrm{2}} } \\ $$$$=\frac{−\frac{{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:+{x}\:−\frac{{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}−{x}}{\left(\mathrm{1}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:=\frac{−\mathrm{2}{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\left(\mathrm{1}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)}\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)\:=\frac{{x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{ln}\mid\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\mathrm{1}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\mid+\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\frac{−\mathrm{2}{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\left(\mathrm{1}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)}×\frac{\mathrm{1}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$=.... \\ $$

Commented by mathmax by abdo last updated on 23/Jul/19

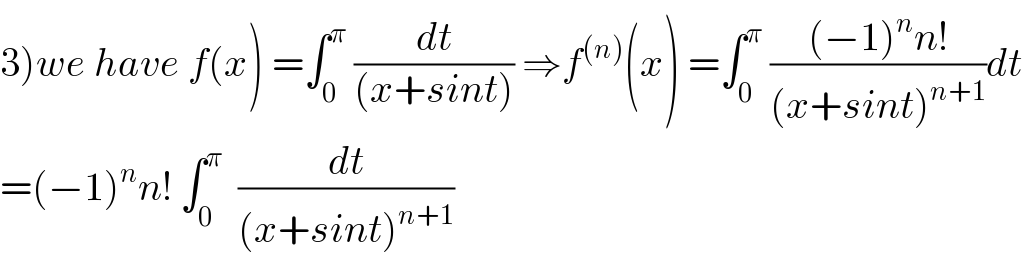
3)we have f(x) =∫_0 ^π (dt/((x+sint))) ⇒f^((n)) (x) =∫_0 ^π (((−1)^n n!)/((x+sint)^(n+1) ))dt =(−1)^n n! ∫_0 ^π (dt/((x+sint)^(n+1) ))

$$\left.\mathrm{3}\right){we}\:{have}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\pi} \:\frac{{dt}}{\left({x}+{sint}\right)}\:\Rightarrow{f}^{\left({n}\right)} \left({x}\right)\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\left({x}+{sint}\right)^{{n}+\mathrm{1}} }{dt} \\ $$$$=\left(−\mathrm{1}\right)^{{n}} {n}!\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{dt}}{\left({x}+{sint}\right)^{{n}+\mathrm{1}} } \\ $$

Commented by mathmax by abdo last updated on 23/Jul/19

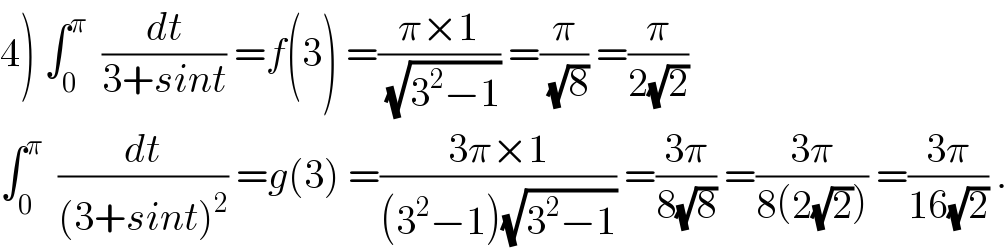
4) ∫_0 ^π (dt/(3+sint)) =f(3) =((π×1)/(√(3^2 −1))) =(π/(√8)) =(π/(2(√2))) ∫_0 ^π (dt/((3+sint)^2 )) =g(3) =((3π×1)/((3^2 −1)(√(3^2 −1)))) =((3π)/(8(√8))) =((3π)/(8(2(√2)))) =((3π)/(16(√2))) .

$$\left.\mathrm{4}\right)\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{dt}}{\mathrm{3}+{sint}}\:={f}\left(\mathrm{3}\right)\:=\frac{\pi×\mathrm{1}}{\sqrt{\mathrm{3}^{\mathrm{2}} −\mathrm{1}}}\:=\frac{\pi}{\sqrt{\mathrm{8}}}\:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\:\frac{{dt}}{\left(\mathrm{3}+{sint}\right)^{\mathrm{2}} }\:={g}\left(\mathrm{3}\right)\:=\frac{\mathrm{3}\pi×\mathrm{1}}{\left(\mathrm{3}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\mathrm{3}^{\mathrm{2}} −\mathrm{1}}}\:=\frac{\mathrm{3}\pi}{\mathrm{8}\sqrt{\mathrm{8}}}\:=\frac{\mathrm{3}\pi}{\mathrm{8}\left(\mathrm{2}\sqrt{\mathrm{2}}\right)}\:=\frac{\mathrm{3}\pi}{\mathrm{16}\sqrt{\mathrm{2}}}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com