Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 35821 by prof Abdo imad last updated on 24/May/18

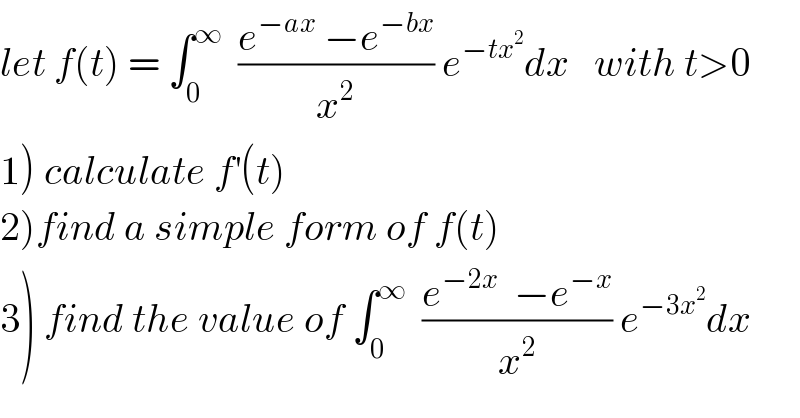
let f(t) = ∫_0 ^∞ ((e^(−ax) −e^(−bx) )/x^2 ) e^(−tx^2 ) dx with t>0 1) calculate f^′ (t) 2)find a simple form of f(t) 3) find the value of ∫_0 ^∞ ((e^(−2x) −e^(−x) )/x^2 ) e^(−3x^2 ) dx

$${let}\:{f}\left({t}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{ax}} \:−{e}^{−{bx}} }{{x}^{\mathrm{2}} }\:{e}^{−{tx}^{\mathrm{2}} } {dx}\:\:\:{with}\:{t}>\mathrm{0} \\ $$ $$\left.\mathrm{1}\right)\:{calculate}\:{f}^{'} \left({t}\right) \\ $$ $$\left.\mathrm{2}\right){find}\:{a}\:{simple}\:{form}\:{of}\:{f}\left({t}\right) \\ $$ $$\left.\mathrm{3}\right)\:{find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−\mathrm{2}{x}} \:\:−{e}^{−{x}} }{{x}^{\mathrm{2}} }\:{e}^{−\mathrm{3}{x}^{\mathrm{2}} } {dx} \\ $$

Commented byprof Abdo imad last updated on 31/May/18

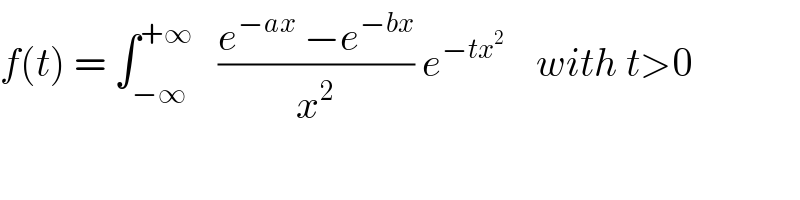
f(t) = ∫_(−∞) ^(+∞) ((e^(−ax) −e^(−bx) )/x^2 ) e^(−tx^2 ) with t>0

$${f}\left({t}\right)\:=\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{e}^{−{ax}} \:−{e}^{−{bx}} }{{x}^{\mathrm{2}} }\:{e}^{−{tx}^{\mathrm{2}} } \:\:\:\:{with}\:{t}>\mathrm{0} \\ $$

Commented byprof Abdo imad last updated on 31/May/18

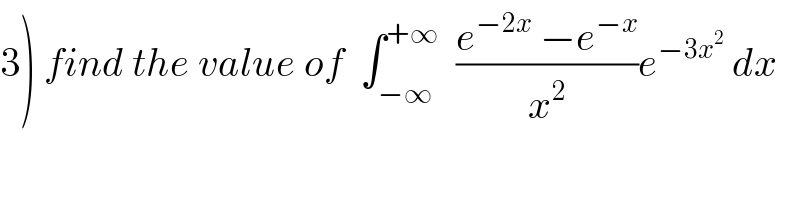
3) find the value of ∫_(−∞) ^(+∞) ((e^(−2x) −e^(−x) )/x^2 )e^(−3x^2 ) dx

$$\left.\mathrm{3}\right)\:{find}\:{the}\:{value}\:{of}\:\:\int_{−\infty} ^{+\infty} \:\:\frac{{e}^{−\mathrm{2}{x}} \:−{e}^{−{x}} }{{x}^{\mathrm{2}} }{e}^{−\mathrm{3}{x}^{\mathrm{2}} } \:{dx} \\ $$

Commented byabdo mathsup 649 cc last updated on 01/Jun/18

we have f^′ (t) = −∫_(−∞) ^(+∞) (e^(−ax) −e^(−bx) ) e^(−tx^2 ) dx = ∫_(−∞) ^(+∞) e^(−bx −tx^2 ) dx −∫_(−∞) ^(+∞) e^(−ax −tx^2 ) dx but ∫_(−∞) ^(+∞) e^(−tx^2 −ax) dx =∫_(−∞) ^(+∞) e^(−{ ((√t)x)^2 +2 (a/(2(√t)))x +(a^2 /(4t)) −(a^2 /(4t))}) dx = ∫_(−∞) ^(+∞) e^(−{ ((√t) x +(a/(2(√t))))^2 } +(a^2 /(4t))) dx = e^(a^2 /(4t)) ∫_(−∞) ^(+∞) e^(−u^2 ) (du/(√t)) (chang. (√t)x +(a/(2(√t))) =u) = (e^(a^2 /(4t)) /(√t)) (√π) ⇒ f(t) = (√π) ∫_. ^t (e^(a^2 /(4u)) /(√u))du +λ changement (√u)=xgive f(t) = (√π) ∫_. ^(√t) (e^(a^2 /(4x^2 )) /x) 2xdx +λ = 2(√π) ∫_. ^(√t) e^(a^2 /(4x^2 )) dx +λ

$${we}\:{have}\:{f}^{'} \left({t}\right)\:=\:−\int_{−\infty} ^{+\infty} \left({e}^{−{ax}} \:−{e}^{−{bx}} \right)\:{e}^{−{tx}^{\mathrm{2}} } {dx} \\ $$ $$=\:\int_{−\infty} ^{+\infty} \:\:\:{e}^{−{bx}\:−{tx}^{\mathrm{2}} } {dx}\:\:−\int_{−\infty} ^{+\infty} \:{e}^{−{ax}\:−{tx}^{\mathrm{2}} } {dx}\:{but} \\ $$ $$\int_{−\infty} ^{+\infty} \:\:{e}^{−{tx}^{\mathrm{2}} −{ax}} \:{dx}\:=\int_{−\infty} ^{+\infty} \:\:\:{e}^{−\left\{\:\left(\sqrt{{t}}{x}\right)^{\mathrm{2}} \:\:+\mathrm{2}\:\frac{{a}}{\mathrm{2}\sqrt{{t}}}{x}\:\:\:+\frac{{a}^{\mathrm{2}} }{\mathrm{4}{t}}\:−\frac{{a}^{\mathrm{2}} }{\mathrm{4}{t}}\right\}} {dx} \\ $$ $$=\:\int_{−\infty} ^{+\infty} \:\:\:{e}^{−\left\{\:\left(\sqrt{{t}}\:{x}\:\:+\frac{{a}}{\mathrm{2}\sqrt{{t}}}\right)^{\mathrm{2}} \right\}\:+\frac{{a}^{\mathrm{2}} }{\mathrm{4}{t}}} \:\:{dx} \\ $$ $$=\:{e}^{\frac{{a}^{\mathrm{2}} }{\mathrm{4}{t}}} \:\:\int_{−\infty} ^{+\infty} \:\:\:\:\:{e}^{−{u}^{\mathrm{2}} } \frac{{du}}{\sqrt{{t}}}\:\left({chang}.\:\sqrt{{t}}{x}\:+\frac{{a}}{\mathrm{2}\sqrt{{t}}}\:={u}\right) \\ $$ $$=\:\:\frac{{e}^{\frac{{a}^{\mathrm{2}} }{\mathrm{4}{t}}} }{\sqrt{{t}}}\:\sqrt{\pi}\:\:\:\Rightarrow\:{f}\left({t}\right)\:=\:\sqrt{\pi}\:\:\int_{.} ^{{t}} \:\:\:\frac{{e}^{\frac{{a}^{\mathrm{2}} }{\mathrm{4}{u}}} }{\sqrt{{u}}}{du}\:+\lambda\: \\ $$ $${changement}\:\sqrt{{u}}={xgive} \\ $$ $${f}\left({t}\right)\:=\:\sqrt{\pi}\:\:\int_{.} ^{\sqrt{{t}}} \:\:\:\frac{{e}^{\frac{{a}^{\mathrm{2}} }{\mathrm{4}{x}^{\mathrm{2}} }} }{{x}}\:\mathrm{2}{xdx}\:+\lambda \\ $$ $$=\:\mathrm{2}\sqrt{\pi}\:\:\:\int_{.} ^{\sqrt{{t}}} \:\:\:\:{e}^{\frac{{a}^{\mathrm{2}} }{\mathrm{4}{x}^{\mathrm{2}} }} \:{dx}\:+\lambda\: \\ $$

Commented byabdo mathsup 649 cc last updated on 01/Jun/18

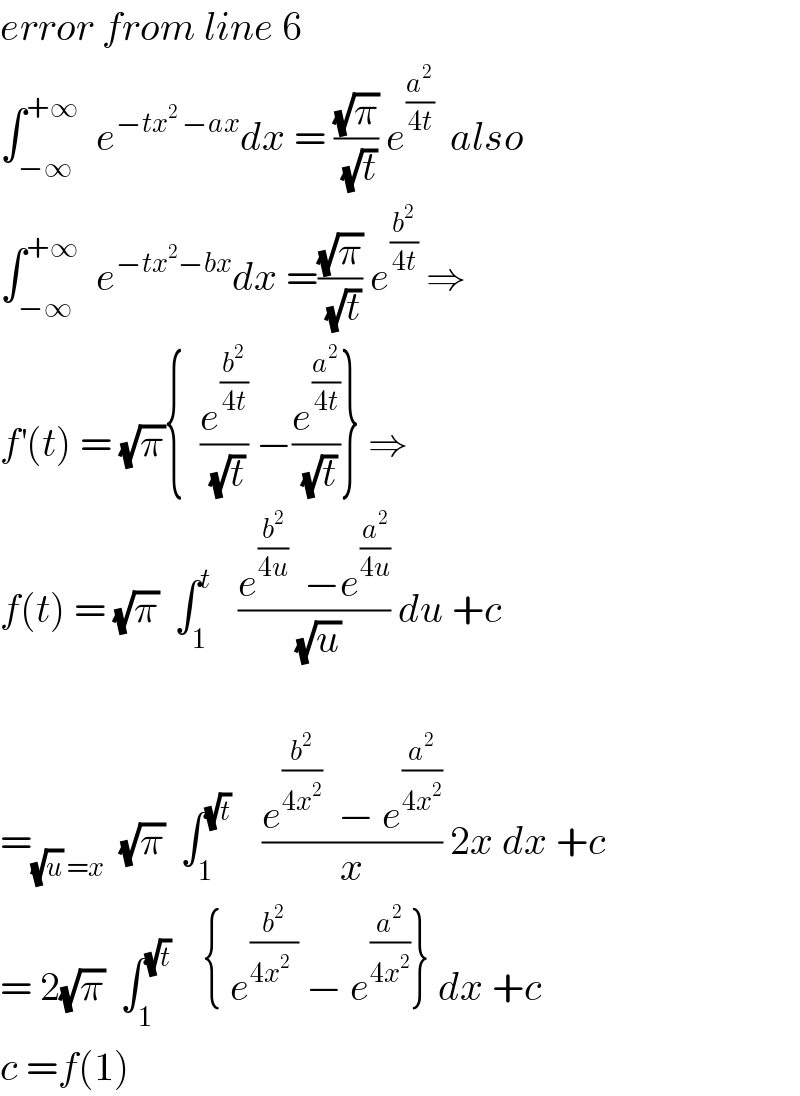
error from line 6 ∫_(−∞) ^(+∞) e^(−tx^2 −ax) dx = ((√π)/(√t)) e^(a^2 /(4t)) also ∫_(−∞) ^(+∞) e^(−tx^2 −bx) dx =((√π)/(√t)) e^(b^2 /(4t)) ⇒ f^′ (t) = (√π){ (e^(b^2 /(4t)) /(√t)) −(e^(a^2 /(4t)) /(√t))} ⇒ f(t) = (√π) ∫_1 ^t ((e^(b^2 /(4u)) −e^(a^2 /(4u)) )/(√u)) du +c =_((√u) =x) (√π) ∫_1 ^(√t) ((e^(b^2 /(4x^2 )) − e^(a^2 /(4x^2 )) )/x) 2x dx +c = 2(√π) ∫_1 ^(√t) { e^(b^2 /(4x^2 )) − e^(a^2 /(4x^2 )) } dx +c c =f(1)

$${error}\:{from}\:{line}\:\mathrm{6} \\ $$ $$\int_{−\infty} ^{+\infty} \:\:{e}^{−{tx}^{\mathrm{2}} \:−{ax}} {dx}\:=\:\frac{\sqrt{\pi}}{\sqrt{{t}}}\:{e}^{\frac{{a}^{\mathrm{2}} }{\mathrm{4}{t}}} \:\:{also} \\ $$ $$\int_{−\infty} ^{+\infty} \:\:{e}^{−{tx}^{\mathrm{2}} −{bx}} {dx}\:=\frac{\sqrt{\pi}}{\sqrt{{t}}}\:{e}^{\frac{{b}^{\mathrm{2}} }{\mathrm{4}{t}}} \:\Rightarrow \\ $$ $${f}^{'} \left({t}\right)\:=\:\sqrt{\pi}\left\{\:\:\frac{{e}^{\frac{{b}^{\mathrm{2}} }{\mathrm{4}{t}}} }{\sqrt{{t}}}\:−\frac{{e}^{\frac{{a}^{\mathrm{2}} }{\mathrm{4}{t}}} }{\sqrt{{t}}}\right\}\:\Rightarrow \\ $$ $${f}\left({t}\right)\:=\:\sqrt{\pi}\:\:\int_{\mathrm{1}} ^{{t}} \:\:\:\frac{{e}^{\frac{{b}^{\mathrm{2}} }{\mathrm{4}{u}}} \:\:−{e}^{\frac{{a}^{\mathrm{2}} }{\mathrm{4}{u}}} }{\sqrt{{u}}}\:{du}\:+{c} \\ $$ $$ \\ $$ $$=_{\sqrt{{u}}\:={x}} \:\:\sqrt{\pi}\:\:\int_{\mathrm{1}} ^{\sqrt{{t}}} \:\:\:\:\frac{{e}^{\frac{{b}^{\mathrm{2}} }{\mathrm{4}{x}^{\mathrm{2}} }} \:\:−\:{e}^{\frac{{a}^{\mathrm{2}} }{\mathrm{4}{x}^{\mathrm{2}} }} }{{x}}\:\mathrm{2}{x}\:{dx}\:+{c} \\ $$ $$=\:\mathrm{2}\sqrt{\pi}\:\:\int_{\mathrm{1}} ^{\sqrt{{t}}} \:\:\:\:\left\{\:{e}^{\frac{{b}^{\mathrm{2}} }{\mathrm{4}{x}^{\mathrm{2}} \:\:}} \:−\:{e}^{\frac{{a}^{\mathrm{2}} }{\mathrm{4}{x}^{\mathrm{2}} }} \right\}\:{dx}\:+{c} \\ $$ $${c}\:={f}\left(\mathrm{1}\right)\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com