Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 206433 by universe last updated on 14/Apr/24

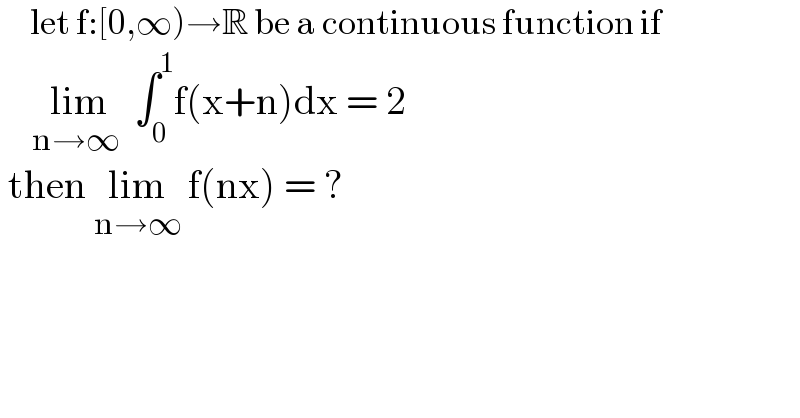
let f:[0,∞)→R be a continuous function if lim_(n→∞ ) ∫_0 ^1 f(x+n)dx = 2 then lim_(n→∞) f(nx) = ?

$$\:\:\:\:\:\mathrm{let}\:\mathrm{f}:\left[\mathrm{0},\infty\right)\rightarrow\mathbb{R}\:\mathrm{be}\:\mathrm{a}\:\mathrm{continuous}\:\mathrm{function}\:\mathrm{if} \\ $$$$\:\:\:\:\underset{\mathrm{n}\rightarrow\infty\:} {\mathrm{lim}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{f}\left(\mathrm{x}+\mathrm{n}\right)\mathrm{dx}\:=\:\mathrm{2} \\ $$$$\:\mathrm{then}\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{f}\left(\mathrm{nx}\right)\:=\:? \\ $$$$\: \\ $$

Answered by Berbere last updated on 14/Apr/24

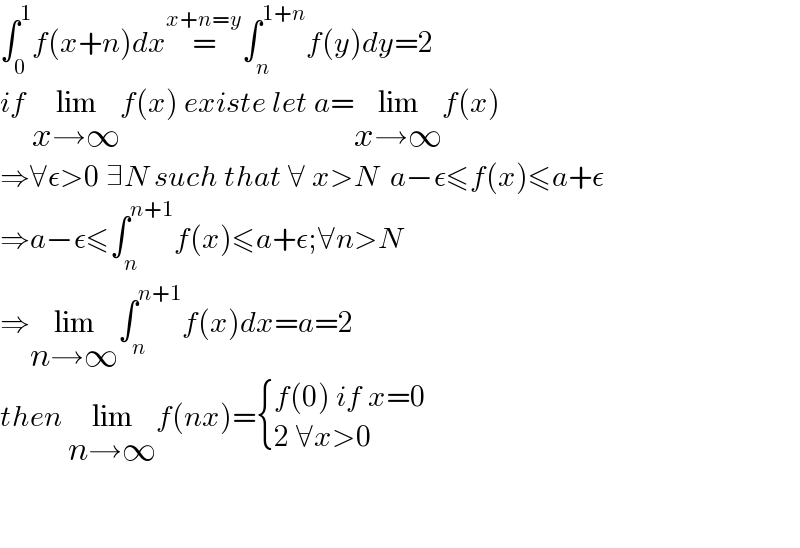
∫_0 ^1 f(x+n)dx=^(x+n=y) ∫_n ^(1+n) f(y)dy=2 if lim_(x→∞) f(x) existe let a=lim_(x→∞) f(x) ⇒∀ε>0 ∃N such that ∀ x>N a−ε≤f(x)≤a+ε ⇒a−ε≤∫_n ^(n+1) f(x)≤a+ε;∀n>N ⇒lim_(n→∞) ∫_n ^(n+1) f(x)dx=a=2 then lim_(n→∞) f(nx)= { ((f(0) if x=0)),((2 ∀x>0)) :}

$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}+{n}\right){dx}\overset{{x}+{n}={y}} {=}\int_{{n}} ^{\mathrm{1}+{n}} {f}\left({y}\right){dy}=\mathrm{2} \\ $$$${if}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}{f}\left({x}\right)\:{existe}\:{let}\:{a}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}{f}\left({x}\right) \\ $$$$\Rightarrow\forall\epsilon>\mathrm{0}\:\exists{N}\:{such}\:{that}\:\forall\:{x}>{N}\:\:{a}−\epsilon\leqslant{f}\left({x}\right)\leqslant{a}+\epsilon \\ $$$$\Rightarrow{a}−\epsilon\leqslant\int_{{n}} ^{{n}+\mathrm{1}} {f}\left({x}\right)\leqslant{a}+\epsilon;\forall{n}>{N} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}\int_{{n}} ^{{n}+\mathrm{1}} {f}\left({x}\right){dx}={a}=\mathrm{2} \\ $$$${then}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}{f}\left({nx}\right)=\begin{cases}{{f}\left(\mathrm{0}\right)\:{if}\:{x}=\mathrm{0}}\\{\mathrm{2}\:\forall{x}>\mathrm{0}}\end{cases} \\ $$$$ \\ $$$$ \\ $$

Commented by aleks041103 last updated on 14/Apr/24

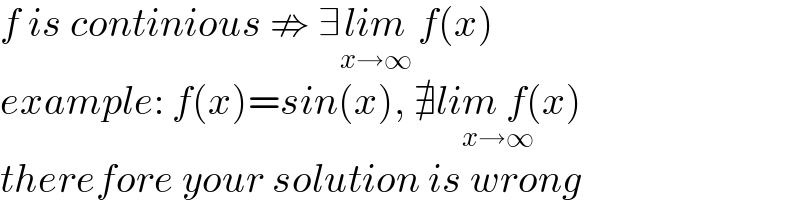
f is continious ⇏ ∃lim_(x→∞) f(x) example: f(x)=sin(x), ∄lim f(x)_(x→∞) therefore your solution is wrong

$${f}\:{is}\:{continious}\:\nRightarrow\:\exists\underset{{x}\rightarrow\infty} {{lim}}\:{f}\left({x}\right) \\ $$$${example}:\:{f}\left({x}\right)={sin}\left({x}\right),\:\underset{{x}\rightarrow\infty} {\nexists{lim}\:{f}\left({x}\right)} \\ $$$${therefore}\:{your}\:{solution}\:{is}\:{wrong} \\ $$

Commented by Berbere last updated on 14/Apr/24

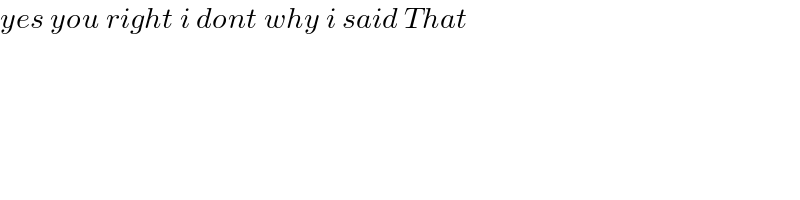
yes you right i dont why i said That

$${yes}\:{you}\:{right}\:{i}\:{dont}\:{why}\:{i}\:{said}\:{That} \\ $$

Answered by Berbere last updated on 14/Apr/24

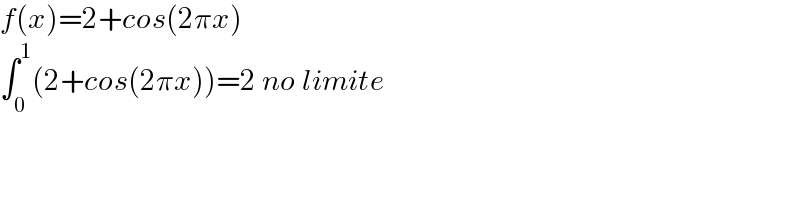
f(x)=2+cos(2πx) ∫_0 ^1 (2+cos(2πx))=2 no limite

$${f}\left({x}\right)=\mathrm{2}+{cos}\left(\mathrm{2}\pi{x}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}+{cos}\left(\mathrm{2}\pi{x}\right)\right)=\mathrm{2}\:{no}\:{limite}\: \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com