Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 41520 by maxmathsup by imad last updated on 08/Aug/18

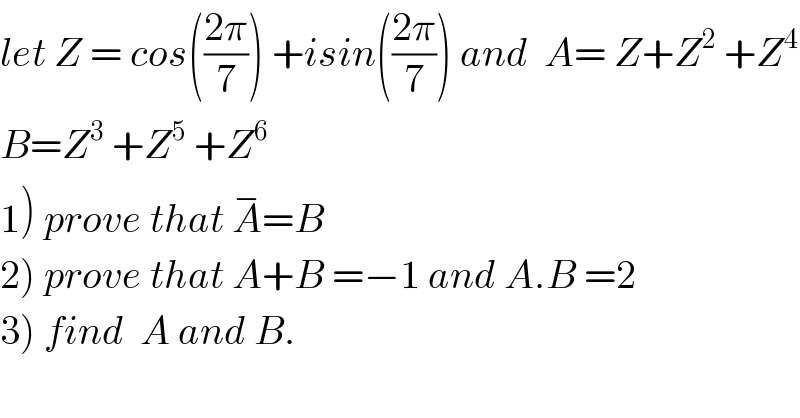
let Z = cos(((2π)/7)) +isin(((2π)/7)) and A= Z+Z^2 +Z^4 B=Z^3 +Z^5 +Z^6 1) prove that A^− =B 2) prove that A+B =−1 and A.B =2 3) find A and B.

$${let}\:{Z}\:=\:{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)\:+{isin}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)\:{and}\:\:{A}=\:{Z}+{Z}^{\mathrm{2}} \:+{Z}^{\mathrm{4}} \\ $$$${B}={Z}^{\mathrm{3}} \:+{Z}^{\mathrm{5}} \:+{Z}^{\mathrm{6}} \\ $$$$\left.\mathrm{1}\right)\:{prove}\:{that}\:\overset{−} {{A}}={B} \\ $$$$\left.\mathrm{2}\right)\:{prove}\:{that}\:{A}+{B}\:=−\mathrm{1}\:{and}\:{A}.{B}\:=\mathrm{2} \\ $$$$\left.\mathrm{3}\right)\:{find}\:\:{A}\:{and}\:{B}. \\ $$$$ \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 09/Aug/18

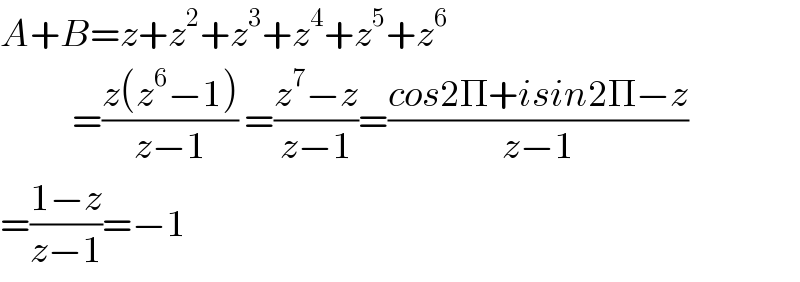
A+B=z+z^2 +z^3 +z^4 +z^5 +z^6 =((z(z^6 −1))/(z−1)) =((z^7 −z)/(z−1))=((cos2Π+isin2Π−z)/(z−1)) =((1−z)/(z−1))=−1

$${A}+{B}={z}+{z}^{\mathrm{2}} +{z}^{\mathrm{3}} +{z}^{\mathrm{4}} +{z}^{\mathrm{5}} +{z}^{\mathrm{6}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{z}\left({z}^{\mathrm{6}} −\mathrm{1}\right)}{{z}−\mathrm{1}}\:=\frac{{z}^{\mathrm{7}} −{z}}{{z}−\mathrm{1}}=\frac{{cos}\mathrm{2}\Pi+{isin}\mathrm{2}\Pi−{z}}{{z}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}−{z}}{{z}−\mathrm{1}}=−\mathrm{1} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 09/Aug/18

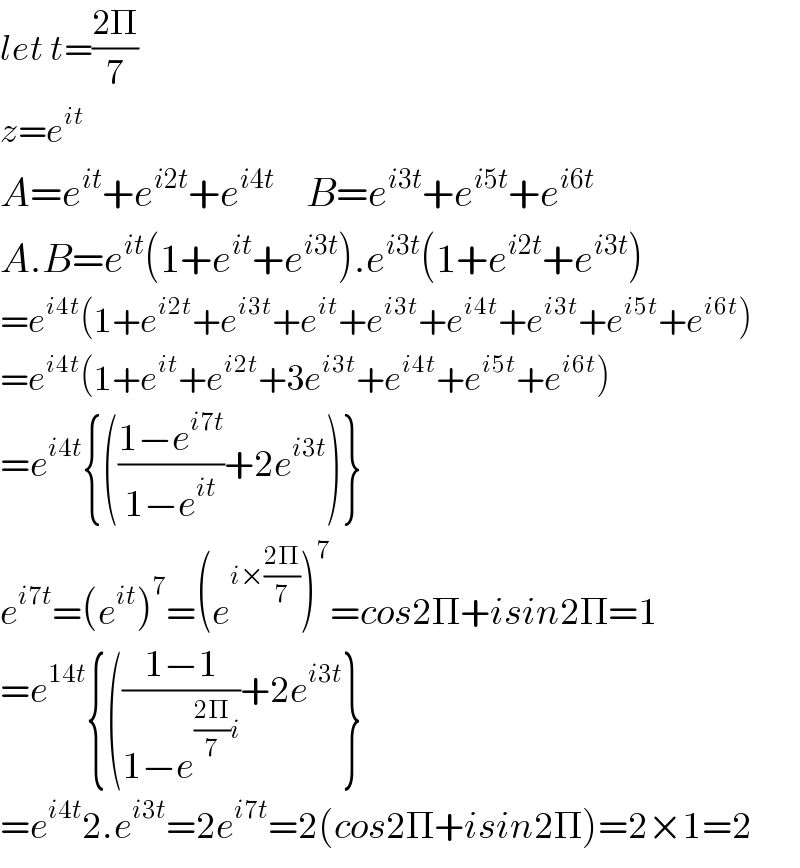
let t=((2Π)/7) z=e^(it) A=e^(it) +e^(i2t) +e^(i4t) B=e^(i3t) +e^(i5t) +e^(i6t) A.B=e^(it) (1+e^(it) +e^(i3t) ).e^(i3t) (1+e^(i2t) +e^(i3t) ) =e^(i4t) (1+e^(i2t) +e^(i3t) +e^(it) +e^(i3t) +e^(i4t) +e^(i3t) +e^(i5t) +e^(i6t) ) =e^(i4t) (1+e^(it) +e^(i2t) +3e^(i3t) +e^(i4t) +e^(i5t) +e^(i6t) ) =e^(i4t) {(((1−e^(i7t) )/(1−e^(it) ))+2e^(i3t) )} e^(i7t) =(e^(it) )^7 =(e^(i×((2Π)/7)) )^7 =cos2Π+isin2Π=1 =e^(14t) {(((1−1)/(1−e^(((2Π)/7)i) ))+2e^(i3t) } =e^(i4t) 2.e^(i3t) =2e^(i7t) =2(cos2Π+isin2Π)=2×1=2

$${let}\:{t}=\frac{\mathrm{2}\Pi}{\mathrm{7}} \\ $$$${z}={e}^{{it}} \\ $$$${A}={e}^{{it}} +{e}^{{i}\mathrm{2}{t}} +{e}^{{i}\mathrm{4}{t}} \:\:\:\:{B}={e}^{{i}\mathrm{3}{t}} +{e}^{{i}\mathrm{5}{t}} +{e}^{{i}\mathrm{6}{t}} \\ $$$${A}.{B}={e}^{{it}} \left(\mathrm{1}+{e}^{{it}} +{e}^{{i}\mathrm{3}{t}} \right).{e}^{{i}\mathrm{3}{t}} \left(\mathrm{1}+{e}^{{i}\mathrm{2}{t}} +{e}^{{i}\mathrm{3}{t}} \right) \\ $$$$={e}^{{i}\mathrm{4}{t}} \left(\mathrm{1}+{e}^{{i}\mathrm{2}{t}} +{e}^{{i}\mathrm{3}{t}} +{e}^{{it}} +{e}^{{i}\mathrm{3}{t}} +{e}^{{i}\mathrm{4}{t}} +{e}^{{i}\mathrm{3}{t}} +{e}^{{i}\mathrm{5}{t}} +{e}^{{i}\mathrm{6}{t}} \right) \\ $$$$={e}^{{i}\mathrm{4}{t}} \left(\mathrm{1}+{e}^{{it}} +{e}^{{i}\mathrm{2}{t}} +\mathrm{3}{e}^{{i}\mathrm{3}{t}} +{e}^{{i}\mathrm{4}{t}} +{e}^{{i}\mathrm{5}{t}} +{e}^{{i}\mathrm{6}{t}} \right) \\ $$$$={e}^{{i}\mathrm{4}{t}} \left\{\left(\frac{\mathrm{1}−{e}^{{i}\mathrm{7}{t}} }{\mathrm{1}−{e}^{{it}} }+\mathrm{2}{e}^{{i}\mathrm{3}{t}} \right)\right\} \\ $$$${e}^{{i}\mathrm{7}{t}} =\left({e}^{{it}} \right)^{\mathrm{7}} =\left({e}^{{i}×\frac{\mathrm{2}\Pi}{\mathrm{7}}} \right)^{\mathrm{7}} ={cos}\mathrm{2}\Pi+{isin}\mathrm{2}\Pi=\mathrm{1} \\ $$$$={e}^{\mathrm{14}{t}} \left\{\left(\frac{\mathrm{1}−\mathrm{1}}{\mathrm{1}−{e}^{\frac{\mathrm{2}\Pi}{\mathrm{7}}{i}} }+\mathrm{2}{e}^{{i}\mathrm{3}{t}} \right\}\right. \\ $$$$={e}^{{i}\mathrm{4}{t}} \mathrm{2}.{e}^{{i}\mathrm{3}{t}} =\mathrm{2}{e}^{{i}\mathrm{7}{t}} =\mathrm{2}\left({cos}\mathrm{2}\Pi+{isin}\mathrm{2}\Pi\right)=\mathrm{2}×\mathrm{1}=\mathrm{2} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 10/Aug/18

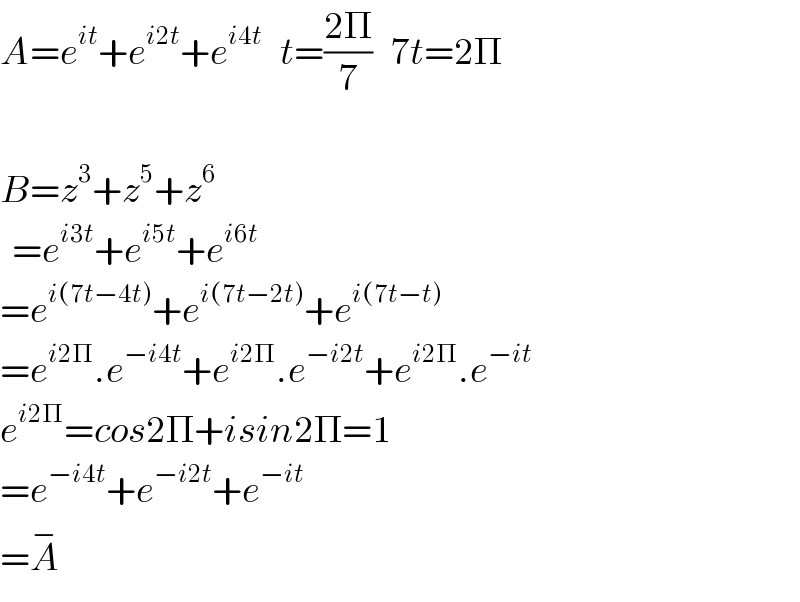
A=e^(it) +e^(i2t) +e^(i4t) t=((2Π)/7) 7t=2Π B=z^3 +z^5 +z^6 =e^(i3t) +e^(i5t) +e^(i6t) =e^(i(7t−4t)) +e^(i(7t−2t)) +e^(i(7t−t)) =e^(i2Π) .e^(−i4t) +e^(i2Π) .e^(−i2t) +e^(i2Π) .e^(−it) e^(i2Π) =cos2Π+isin2Π=1 =e^(−i4t) +e^(−i2t) +e^(−it) =A^−

$${A}={e}^{{it}} +{e}^{{i}\mathrm{2}{t}} +{e}^{{i}\mathrm{4}{t}} \:\:\:{t}=\frac{\mathrm{2}\Pi}{\mathrm{7}}\:\:\:\mathrm{7}{t}=\mathrm{2}\Pi \\ $$$$ \\ $$$${B}={z}^{\mathrm{3}} +{z}^{\mathrm{5}} +{z}^{\mathrm{6}} \\ $$$$\:\:={e}^{{i}\mathrm{3}{t}} +{e}^{{i}\mathrm{5}{t}} +{e}^{{i}\mathrm{6}{t}} \\ $$$$={e}^{{i}\left(\mathrm{7}{t}−\mathrm{4}{t}\right)} +{e}^{{i}\left(\mathrm{7}{t}−\mathrm{2}{t}\right)} +{e}^{{i}\left(\mathrm{7}{t}−{t}\right)} \\ $$$$={e}^{{i}\mathrm{2}\Pi} .{e}^{−{i}\mathrm{4}{t}} +{e}^{{i}\mathrm{2}\Pi} .{e}^{−{i}\mathrm{2}{t}} +{e}^{{i}\mathrm{2}\Pi} .{e}^{−{it}} \:\: \\ $$$${e}^{{i}\mathrm{2}\Pi} ={cos}\mathrm{2}\Pi+{isin}\mathrm{2}\Pi=\mathrm{1} \\ $$$$={e}^{−{i}\mathrm{4}{t}} +{e}^{−{i}\mathrm{2}{t}} +{e}^{−{it}} \\ $$$$=\overset{−} {{A}} \\ $$

Commented by rahul 19 last updated on 10/Aug/18

nice!

$$\mathrm{nice}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com