
Question Number 62812 by mathmax by abdo last updated on 25/Jun/19
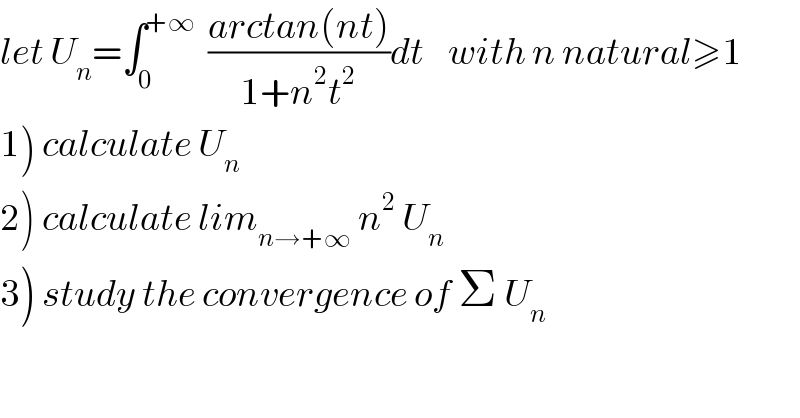
$${let}\:{U}_{{n}} =\int_{\mathrm{0}} ^{+\infty} \:\:\frac{{arctan}\left({nt}\right)}{\mathrm{1}+{n}^{\mathrm{2}} {t}^{\mathrm{2}} }{dt}\:\:\:\:{with}\:{n}\:{natural}\geqslant\mathrm{1} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{U}_{{n}} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:{lim}_{{n}\rightarrow+\infty} \:{n}^{\mathrm{2}} \:{U}_{{n}} \\ $$$$\left.\mathrm{3}\right)\:{study}\:{the}\:{convergence}\:{of}\:\Sigma\:{U}_{{n}} \\ $$
Commented by mathmax by abdo last updated on 26/Jun/19
![1) by parts u^′ =(1/(1+n^2 t^2 )) and v =arctan(nt) ⇒ U_n =[(1/n) (arctan(nt))^2 ]_0 ^(+∞) −∫_0 ^∞ (1/n) arctan(nt)(n/(1+n^2 t^2 ))dt =(π^2 /(4n)) −∫_0 ^∞ ((arctan(nt))/(1+n^2 t^2 ))dt =(π^2 /(4n)) −U_n ⇒2U_n =(π^2 /(4n)) ⇒ U_n =(π^2 /(8n)) 2)we have n^2 U_n =((nπ^2 )/8) ⇒lim_(n→+∞) n^2 U_n =+∞ 3)the numeric serie Σ(π^2 /(8n)) diverges ⇒Σ U_n diverges.](Q62872.png)
$$\left.\mathrm{1}\right)\:{by}\:{parts}\:\:{u}^{'} \:=\frac{\mathrm{1}}{\mathrm{1}+{n}^{\mathrm{2}} {t}^{\mathrm{2}} }\:\:{and}\:{v}\:={arctan}\left({nt}\right)\:\Rightarrow \\ $$$${U}_{{n}} =\left[\frac{\mathrm{1}}{{n}}\:\left({arctan}\left({nt}\right)\right)^{\mathrm{2}} \right]_{\mathrm{0}} ^{+\infty} \:−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{n}}\:{arctan}\left({nt}\right)\frac{{n}}{\mathrm{1}+{n}^{\mathrm{2}} {t}^{\mathrm{2}} }{dt} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{4}{n}}\:−\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctan}\left({nt}\right)}{\mathrm{1}+{n}^{\mathrm{2}} {t}^{\mathrm{2}} }{dt}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{4}{n}}\:−{U}_{{n}} \:\Rightarrow\mathrm{2}{U}_{{n}} =\frac{\pi^{\mathrm{2}} }{\mathrm{4}{n}}\:\Rightarrow\:{U}_{{n}} =\frac{\pi^{\mathrm{2}} }{\mathrm{8}{n}} \\ $$$$\left.\mathrm{2}\right){we}\:{have}\:{n}^{\mathrm{2}} \:{U}_{{n}} =\frac{{n}\pi^{\mathrm{2}} }{\mathrm{8}}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} {n}^{\mathrm{2}} {U}_{{n}} =+\infty \\ $$$$\left.\mathrm{3}\right){the}\:{numeric}\:{serie}\:\Sigma\frac{\pi^{\mathrm{2}} }{\mathrm{8}{n}}\:\:{diverges}\:\Rightarrow\Sigma\:{U}_{{n}} \:{diverges}. \\ $$
