
Previous in Relation and Functions Next in Relation and Functions
Question Number 78261 by msup trace by abdo last updated on 15/Jan/20
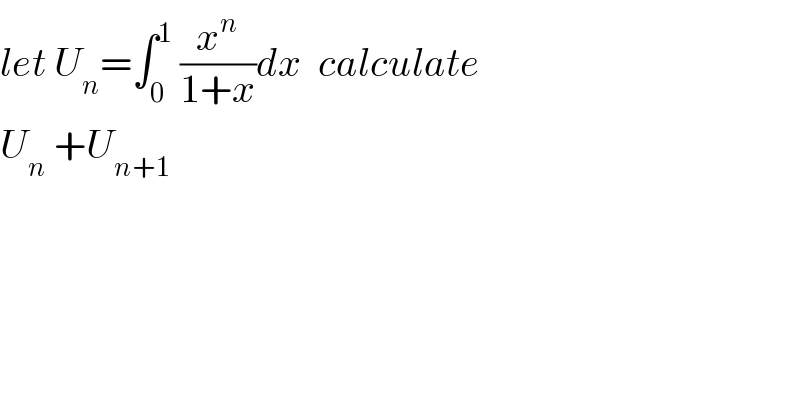
$${let}\:{U}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}^{{n}} }{\mathrm{1}+{x}}{dx}\:\:{calculate} \\ $$$${U}_{{n}} \:+{U}_{{n}+\mathrm{1}} \\ $$
Commented by jagoll last updated on 15/Jan/20
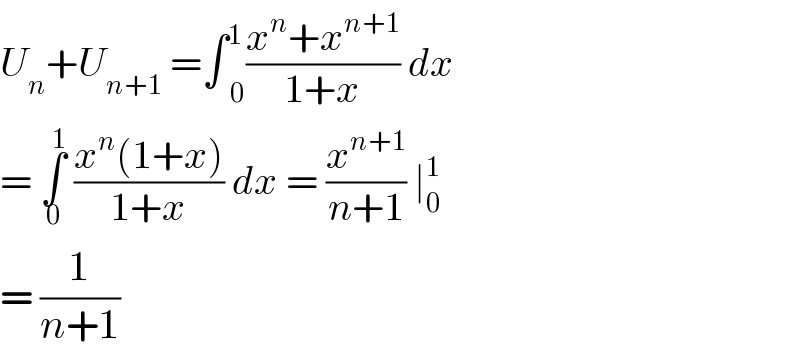
$${U}_{{n}} +{U}_{{n}+\mathrm{1}} \:=\int\underset{\mathrm{0}} {\overset{\mathrm{1}\:} {\:}}\frac{{x}^{{n}} +{x}^{{n}+\mathrm{1}} }{\mathrm{1}+{x}}\:{dx} \\ $$$$=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{{x}^{{n}} \left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}}\:{dx}\:=\:\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\:\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$
Commented by mr W last updated on 16/Jan/20

$${U}_{{n}} =? \\ $$
Commented by john santu last updated on 16/Jan/20
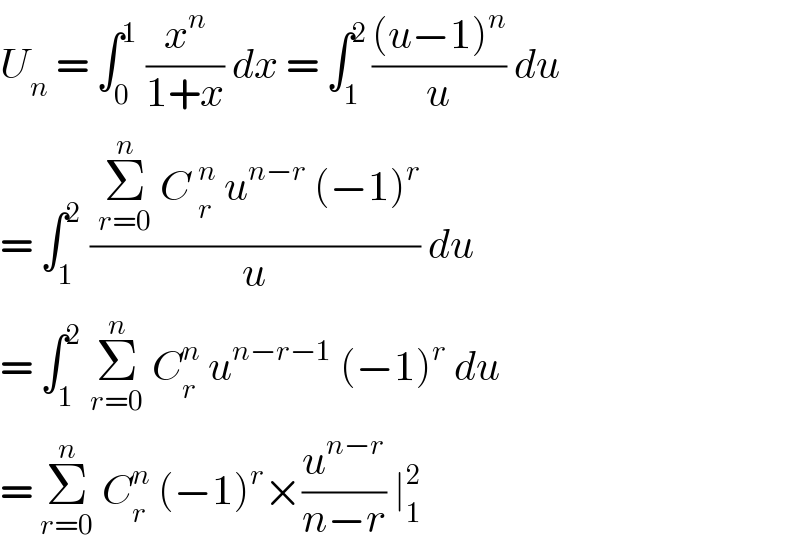
$${U}_{{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}^{{n}} }{\mathrm{1}+{x}}\:{dx}\:=\:\int_{\mathrm{1}} ^{\mathrm{2}\:} \frac{\left({u}−\mathrm{1}\right)^{{n}} }{{u}}\:{du} \\ $$$$=\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{\:\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\:{C}\:_{{r}} ^{{n}} \:{u}^{{n}−{r}} \:\left(−\mathrm{1}\right)^{{r}} }{{u}}\:{du} \\ $$$$=\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\:{C}_{{r}} ^{{n}} \:{u}^{{n}−{r}−\mathrm{1}} \:\left(−\mathrm{1}\right)^{{r}} \:{du} \\ $$$$=\:\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\:{C}_{{r}} ^{{n}} \:\left(−\mathrm{1}\right)^{{r}} ×\frac{{u}^{{n}−{r}} }{{n}−{r}}\:\mid_{\mathrm{1}} ^{\mathrm{2}} \: \\ $$
