
Previous in Relation and Functions Next in Relation and Functions
Question Number 63651 by mathmax by abdo last updated on 06/Jul/19
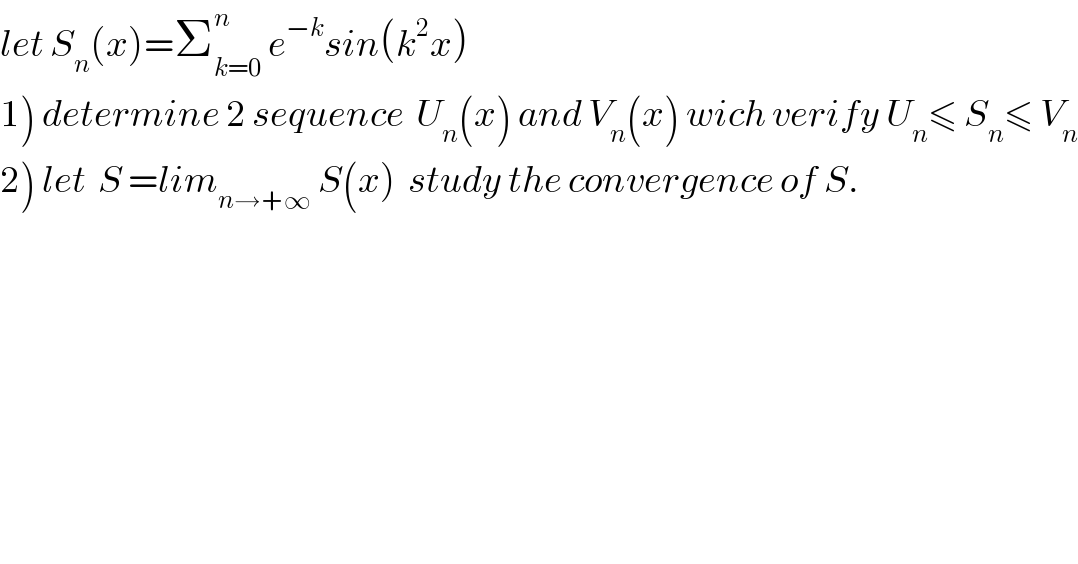
$${let}\:{S}_{{n}} \left({x}\right)=\sum_{{k}=\mathrm{0}} ^{{n}} \:{e}^{−{k}} {sin}\left({k}^{\mathrm{2}} {x}\right) \\ $$$$\left.\mathrm{1}\right)\:{determine}\:\mathrm{2}\:{sequence}\:\:{U}_{{n}} \left({x}\right)\:{and}\:{V}_{{n}} \left({x}\right)\:{wich}\:{verify}\:{U}_{{n}} \leqslant\:{S}_{{n}} \leqslant\:{V}_{{n}} \\ $$$$\left.\mathrm{2}\right)\:{let}\:\:{S}\:={lim}_{{n}\rightarrow+\infty} \:{S}\left({x}\right)\:\:{study}\:{the}\:{convergence}\:{of}\:{S}. \\ $$
