Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 3385 by Filup last updated on 12/Dec/15

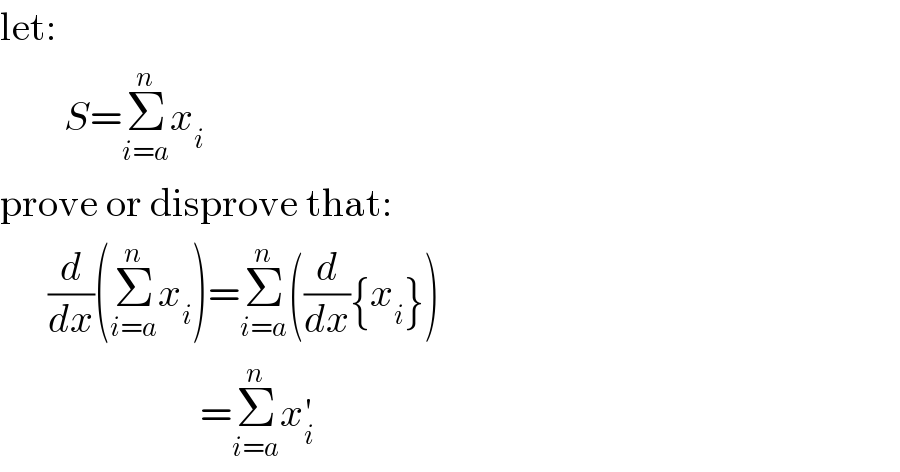
let: S=Σ_(i=a) ^n x_i prove or disprove that: (d/dx)(Σ_(i=a) ^n x_i )=Σ_(i=a) ^n ((d/dx){x_i }) =Σ_(i=a) ^n x_i ^′

$$\mathrm{let}: \\ $$$$\:\:\:\:\:\:\:\:{S}=\underset{{i}={a}} {\overset{{n}} {\sum}}{x}_{{i}} \\ $$$$\mathrm{prove}\:\mathrm{or}\:\mathrm{disprove}\:\mathrm{that}: \\ $$$$\:\:\:\:\:\:\frac{{d}}{{dx}}\left(\underset{{i}={a}} {\overset{{n}} {\sum}}{x}_{{i}} \right)=\underset{{i}={a}} {\overset{{n}} {\sum}}\left(\frac{{d}}{{dx}}\left\{{x}_{{i}} \right\}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{i}={a}} {\overset{{n}} {\sum}}{x}_{{i}} ^{'} \\ $$

Commented by prakash jain last updated on 12/Dec/15

Some of two function which are not differentiable at x=x_0 may be differentiable at x=x_0 .

$$\mathrm{Some}\:\mathrm{of}\:\mathrm{two}\:\mathrm{function}\:\mathrm{which}\:\mathrm{are}\:\mathrm{not}\:\mathrm{differentiable} \\ $$$$\mathrm{at}\:{x}={x}_{\mathrm{0}} \:\mathrm{may}\:\mathrm{be}\:\mathrm{differentiable}\:\mathrm{at}\:{x}={x}_{\mathrm{0}} . \\ $$

Commented by Filup last updated on 12/Dec/15

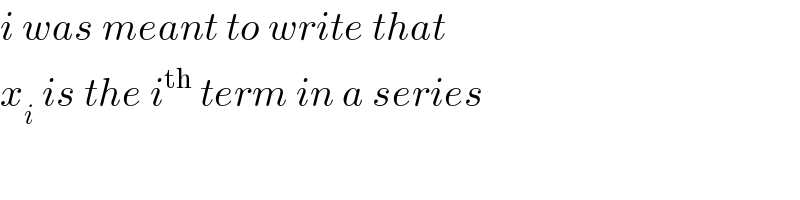
i was meant to write that x_i is the i^(th) term in a series

$${i}\:{was}\:{meant}\:{to}\:{write}\:{that} \\ $$$${x}_{{i}} \:{is}\:{the}\:{i}^{\mathrm{th}} \:{term}\:{in}\:{a}\:{series} \\ $$

Commented by prakash jain last updated on 12/Dec/15

It does make a difference. If x_i i^(th) term in series. It is a still function of x.

$$\mathrm{It}\:\mathrm{does}\:\mathrm{make}\:\mathrm{a}\:\mathrm{difference}.\:\mathrm{If}\:{x}_{{i}} \:{i}^{{th}} \:\mathrm{term}\:\mathrm{in} \\ $$$$\mathrm{series}.\:\mathrm{It}\:\mathrm{is}\:\mathrm{a}\:\mathrm{still}\:\mathrm{function}\:\mathrm{of}\:{x}. \\ $$

Commented by Filup last updated on 12/Dec/15

i see. hmm... so is there ever a time such that the above is true? other than x_i =constant

$$\mathrm{i}\:\mathrm{see}.\:\mathrm{hmm}...\:\mathrm{so}\:\mathrm{is}\:\mathrm{there}\:\mathrm{ever}\:\mathrm{a}\:\mathrm{time} \\ $$$$\mathrm{such}\:\mathrm{that}\:\mathrm{the}\:\mathrm{above}\:\mathrm{is}\:\mathrm{true}? \\ $$$$\mathrm{other}\:\mathrm{than}\:{x}_{{i}} =\mathrm{constant} \\ $$

Commented by prakash jain last updated on 12/Dec/15

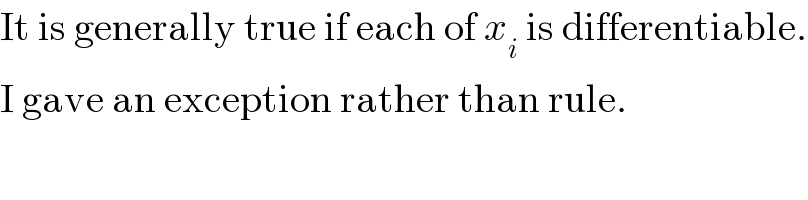
It is generally true if each of x_i is differentiable. I gave an exception rather than rule.

$$\mathrm{It}\:\mathrm{is}\:\mathrm{generally}\:\mathrm{true}\:\mathrm{if}\:\mathrm{each}\:\mathrm{of}\:{x}_{{i}} \:\mathrm{is}\:\mathrm{differentiable}. \\ $$$$\mathrm{I}\:\mathrm{gave}\:\mathrm{an}\:\mathrm{exception}\:\mathrm{rather}\:\mathrm{than}\:\mathrm{rule}. \\ $$

Commented by Filup last updated on 12/Dec/15

Ah I understand now, thanks!

$$\mathrm{Ah}\:\mathrm{I}\:\mathrm{understand}\:\mathrm{now},\:\mathrm{thanks}! \\ $$

Commented by prakash jain last updated on 12/Dec/15

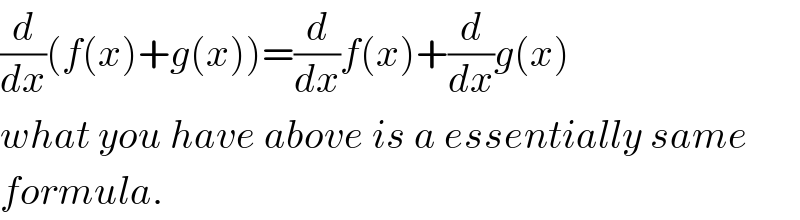
(d/dx)(f(x)+g(x))=(d/dx)f(x)+(d/dx)g(x) what you have above is a essentially same formula.

$$\frac{{d}}{{dx}}\left({f}\left({x}\right)+{g}\left({x}\right)\right)=\frac{{d}}{{dx}}{f}\left({x}\right)+\frac{{d}}{{dx}}{g}\left({x}\right) \\ $$$${what}\:{you}\:{have}\:{above}\:{is}\:{a}\:{essentially}\:{same} \\ $$$${formula}. \\ $$

Answered by prakash jain last updated on 12/Dec/15

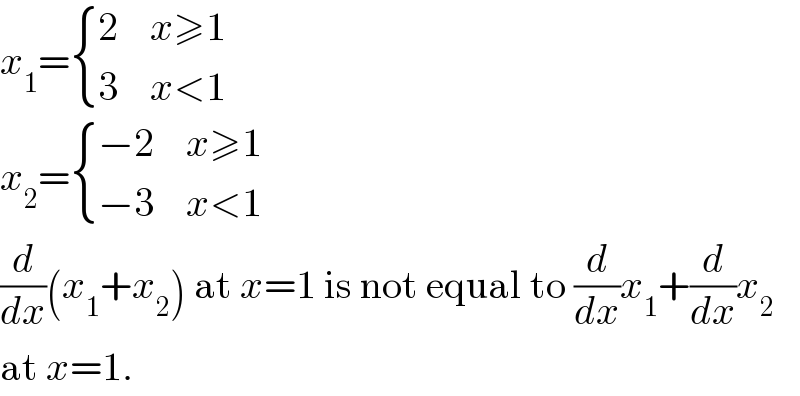
x_1 = { (2,(x≥1)),(3,(x<1)) :} x_2 = { ((−2),(x≥1)),((−3),(x<1)) :} (d/dx)(x_1 +x_2 ) at x=1 is not equal to (d/dx)x_1 +(d/dx)x_2 at x=1.

$${x}_{\mathrm{1}} =\begin{cases}{\mathrm{2}}&{{x}\geqslant\mathrm{1}}\\{\mathrm{3}}&{{x}<\mathrm{1}}\end{cases} \\ $$$${x}_{\mathrm{2}} =\begin{cases}{−\mathrm{2}}&{{x}\geqslant\mathrm{1}}\\{−\mathrm{3}}&{{x}<\mathrm{1}}\end{cases} \\ $$$$\frac{{d}}{{dx}}\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right)\:\mathrm{at}\:{x}=\mathrm{1}\:\mathrm{is}\:\mathrm{not}\:\mathrm{equal}\:\mathrm{to}\:\frac{{d}}{{dx}}{x}_{\mathrm{1}} +\frac{{d}}{{dx}}{x}_{\mathrm{2}} \\ $$$$\mathrm{at}\:{x}=\mathrm{1}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com