
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 190602 by uchihayahia last updated on 07/Apr/23

$$ \\ $$$$\: \\ $$$$\:{let}\:{S}=\left\{{a},{b},{c},{d},{e},{f}\right\} \\ $$$$\:{if}\:{we}\:{take}\:{any}\:{subset}\:{S}\:\left({same}\:{subset}\:{is}\:{allowed}\right), \\ $$$$\:{it}\:{also}\:{can}\:{be}\:{S},\:{which}\:{will}\:{form}\:{S}\:{if}\:{we}\:{join}\:{them}, \\ $$$${order}\:{of}\:{operation}\:{does}\:{not}\:{matter} \\ $$$$\:\left(\left\{{a},{b},{c},{d}\right\},\left\{{d},{e},{f}\right\}\right)\:{is}\:{the}\:{same}\:{as} \\ $$$$\:\left(\left\{{d},{e},{f}\right\},\left\{{a},{b},{c},{d}\right\}\right) \\ $$$$\:{how}\:{many}\:{ways}\:{can}\:{we}\:{choose}? \\ $$$$\: \\ $$$$ \\ $$
Answered by mr W last updated on 07/Apr/23
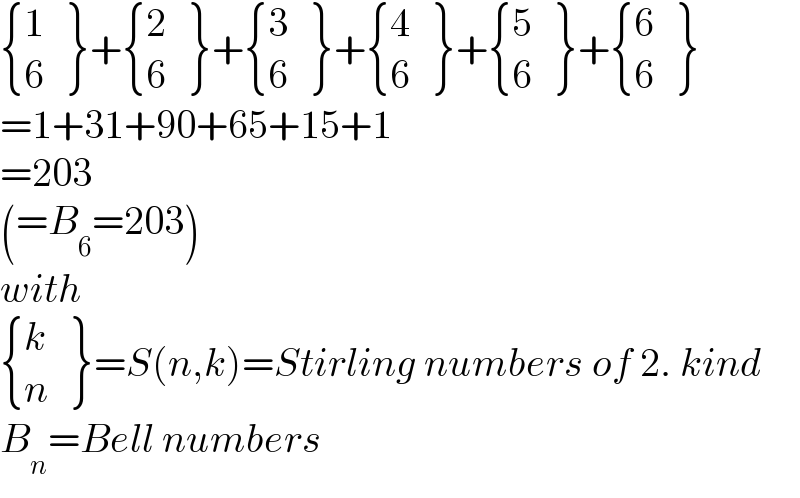
$$\begin{cases}{\mathrm{1}}\\{\mathrm{6}}\end{cases}\left.\begin{matrix}{}\\{}\end{matrix}\right\}+\begin{cases}{\mathrm{2}}\\{\mathrm{6}}\end{cases}\left.\begin{matrix}{}\\{}\end{matrix}\right\}+\begin{cases}{\mathrm{3}}\\{\mathrm{6}}\end{cases}\left.\begin{matrix}{}\\{}\end{matrix}\right\}+\begin{cases}{\mathrm{4}}\\{\mathrm{6}}\end{cases}\left.\begin{matrix}{}\\{}\end{matrix}\right\}+\begin{cases}{\mathrm{5}}\\{\mathrm{6}}\end{cases}\left.\begin{matrix}{}\\{}\end{matrix}\right\}+\begin{cases}{\mathrm{6}}\\{\mathrm{6}}\end{cases}\left.\begin{matrix}{}\\{}\end{matrix}\right\} \\ $$$$=\mathrm{1}+\mathrm{31}+\mathrm{90}+\mathrm{65}+\mathrm{15}+\mathrm{1} \\ $$$$=\mathrm{203} \\ $$$$\left(={B}_{\mathrm{6}} =\mathrm{203}\right) \\ $$$${with} \\ $$$$\begin{cases}{{k}}\\{{n}}\end{cases}\left.\begin{matrix}{}\\{}\end{matrix}\right\}={S}\left({n},{k}\right)={Stirling}\:{numbers}\:{of}\:\mathrm{2}.\:{kind} \\ $$$${B}_{{n}} ={Bell}\:{numbers} \\ $$
Commented by uchihayahia last updated on 07/Apr/23

$${for}\:{example} \\ $$$$\:{subset}\:{with}\:\mathrm{0}\:{element}\: \\ $$$$\:{and}\:{subset}\:{with}\:\mathrm{6}\:{elements}\:{there}\:{is}\:\mathrm{1}\:{choice} \\ $$$$\:{subset}\:{with}\:\mathrm{1}\:{element} \\ $$$$\:{and}\:{subset}\:{with}\:\mathrm{5}\:{elements}\:{there}\:{is}\:\mathrm{6}\:{choices} \\ $$$$\:{subset}\:{with}\:\mathrm{1}\:{element} \\ $$$$\:{and}\:{subset}\:{with}\:\mathrm{6}\:{elements}\:{there}\:{is}\:\mathrm{6}\:{choices} \\ $$$$\:{subset}\:{with}\:\mathrm{2}\:{element} \\ $$$$\:{and}\:{subset}\:{with}\:\mathrm{6}\:{elements}\:{there}\:{is}\:\mathrm{15}\:{choices} \\ $$$$\:{subset}\:{with}\:\mathrm{2}\:{element} \\ $$$$\:{and}\:{subset}\:{with}\:\mathrm{5}\:{elements}\:{there}\:{is}\:\mathrm{30}\:{choices} \\ $$$$\:{subset}\:{with}\:\mathrm{2}\:{element} \\ $$$$\:{and}\:{subset}\:{with}\:\mathrm{4}\:{elements}\:{there}\:{is}\:\mathrm{15}\:{choices} \\ $$$$\:\:{so}\:{on}\:{and}\:{so}\:{forth} \\ $$$$ \\ $$$$ \\ $$
Commented by mr W last updated on 07/Apr/23

Commented by uchihayahia last updated on 07/Apr/23
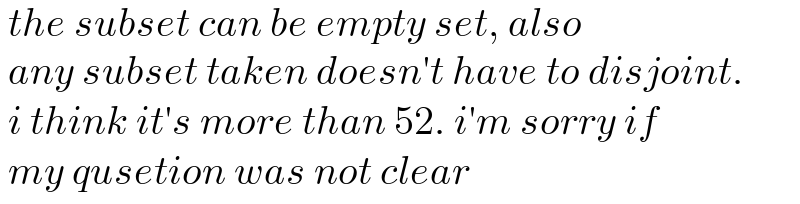
$$\:{the}\:{subset}\:{can}\:{be}\:{empty}\:{set},\:{also} \\ $$$$\:{any}\:{subset}\:{taken}\:{doesn}'{t}\:{have}\:{to}\:{disjoint}. \\ $$$$\:{i}\:{think}\:{it}'{s}\:{more}\:{than}\:\mathrm{52}.\:{i}'{m}\:{sorry}\:{if} \\ $$$$\:{my}\:{qusetion}\:{was}\:{not}\:{clear} \\ $$
Commented by mr W last updated on 07/Apr/23

$${i}'{m}\:{sorry}\:{that}\:{it}\:{is}\:{still}\:{not}\:{clear}\:{to} \\ $$$${me}.\:{can}\:{you}\:{explain}\:{with}\:{some}\: \\ $$$${examples}\:{what}\:{is}\:{not}\:{included}\:{in} \\ $$$${my}\:{solution}\:{and}\:{what}\:{you}\:{mean} \\ $$$${with}\:{empty}\:{subsets}? \\ $$$${btw}:\:{i}\:{misread}\:{that}\:{the}\:{set}\:{has}\:{only} \\ $$$$\mathrm{5}\:{elements}.\:{but}\:{it}\:{has}\:\mathrm{6}\:{elements}. \\ $$$${this}\:{is}\:{fixed}. \\ $$
