
Question Number 31053 by abdo imad last updated on 02/Mar/18
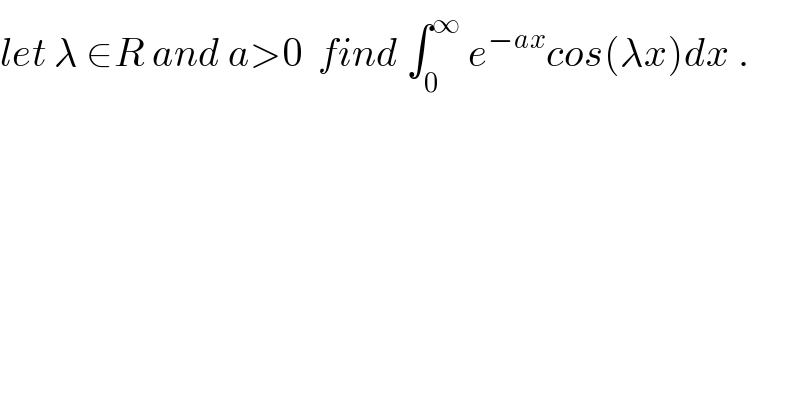
$${let}\:\lambda\:\in{R}\:{and}\:{a}>\mathrm{0}\:\:{find}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{ax}} {cos}\left(\lambda{x}\right){dx}\:. \\ $$
Commented by abdo imad last updated on 03/Mar/18
![let put I=∫_0 ^∞ e^(−ax) cos(λx)dx I=Re( ∫_0 ^∞ e^(−ax) e^(iλx) dx)=Re( ∫_0 ^∞ e^((−a+iλ)x) dx)but ∫_0 ^∞ e^((−a+iλ)x) dx=[ (1/(−a+iλ))e^((−a+iλ)x) ]_(x=0) ^(x→+∞) =((−1)/(−a+iλ))= (1/(a−λi)) =((a+λi)/(a^2 +λ^2 )) ⇒ I= (a/(a^2 +λ^2 )) .](Q31225.png)
$${let}\:{put}\:{I}=\int_{\mathrm{0}} ^{\infty} {e}^{−{ax}} {cos}\left(\lambda{x}\right){dx} \\ $$$${I}={Re}\left(\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{ax}} {e}^{{i}\lambda{x}} {dx}\right)={Re}\left(\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{\left(−{a}+{i}\lambda\right){x}} {dx}\right){but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{\left(−{a}+{i}\lambda\right){x}} {dx}=\left[\:\frac{\mathrm{1}}{−{a}+{i}\lambda}{e}^{\left(−{a}+{i}\lambda\right){x}} \right]_{{x}=\mathrm{0}} ^{{x}\rightarrow+\infty} \\ $$$$=\frac{−\mathrm{1}}{−{a}+{i}\lambda}=\:\frac{\mathrm{1}}{{a}−\lambda{i}}\:=\frac{{a}+\lambda{i}}{{a}^{\mathrm{2}} \:+\lambda^{\mathrm{2}} }\:\Rightarrow\:{I}=\:\frac{{a}}{{a}^{\mathrm{2}} \:+\lambda^{\mathrm{2}} }\:. \\ $$
