
Question Number 51994 by maxmathsup by imad last updated on 01/Jan/19
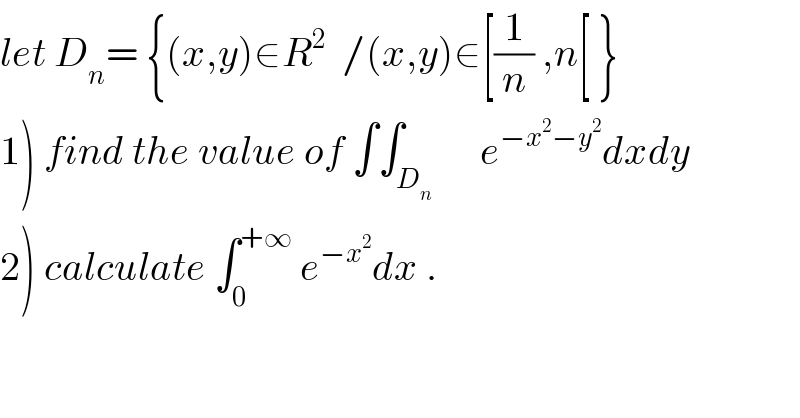
$${let}\:{D}_{{n}} =\:\left\{\left({x},{y}\right)\in{R}^{\mathrm{2}} \:\:/\left({x},{y}\right)\in\left[\frac{\mathrm{1}}{{n}}\:,{n}\left[\:\right\}\right.\right. \\ $$$$\left.\mathrm{1}\right)\:{find}\:{the}\:{value}\:{of}\:\int\int_{{D}_{{n}} } \:\:\:\:\:{e}^{−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} } {dxdy} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{+\infty} \:{e}^{−{x}^{\mathrm{2}} } {dx}\:. \\ $$
Commented by Abdo msup. last updated on 03/Jan/19
![changement x=r cosθ and y=r sinθ give x^2 +y^2 =r^2 but (1/n^2 )≤x^2 ≤n^2 and (1/n^2 )≤y^2 ≤n^2 ⇒ (2/n^2 )≤x^2 +y^2 ≤2n^2 ⇒(2/n^2 ) ≤r^2 ≤2n^2 ((√2)/n) ≤r≤(√2)n also x≥0 and y≥0 ⇒0≤θ≤(π/2) ∫∫_(D_n ) e^(−x^2 −y^2 ) dxdy =∫∫_(((√2)/n)≤r<(√2)n and 0≤θ≤(π/2)) e^(−r^2 ) rdr dθ =(π/2) (−(1/2))[ e^(−r^2 ) ]_((√2)/n) ^((√2)n) =(π/4){ −e^(−2n^2 ) +e^(−(2/n^2 )) } 2) we have ∫∫_D_n e^(−x^2 −y^2 ) dxdy =∫_(1/n) ^n e^(−x^2 ) dx.∫_(1/n) ^n e^(−y^2 ) dy =(∫_(1/n) ^n e^(−x^2 ) dx)^2 ⇒ lim_(n→+∞) (∫_(1/n) ^n e^(−x^2 ) dx)^2 =lim_(n→+∞) D_n =(π/4) ⇒ (∫_0 ^(+∞) e^(−x^2 ) dx)^2 =(π/4) ⇒∫_0 ^∞ e^(−x^2 ) dx =((√π)/2) .](Q52162.png)
$${changement}\:{x}={r}\:{cos}\theta\:{and}\:{y}={r}\:{sin}\theta\:{give} \\ $$$${x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \:{but}\:\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\leqslant{x}^{\mathrm{2}} \leqslant{n}^{\mathrm{2}} \:{and}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\leqslant{y}^{\mathrm{2}} \leqslant{n}^{\mathrm{2}} \:\Rightarrow \\ $$$$\frac{\mathrm{2}}{{n}^{\mathrm{2}} }\leqslant{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \leqslant\mathrm{2}{n}^{\mathrm{2}} \:\Rightarrow\frac{\mathrm{2}}{{n}^{\mathrm{2}} }\:\leqslant{r}^{\mathrm{2}} \:\leqslant\mathrm{2}{n}^{\mathrm{2}} \:\: \\ $$$$\frac{\sqrt{\mathrm{2}}}{{n}}\:\leqslant{r}\leqslant\sqrt{\mathrm{2}}{n}\:\:{also}\:{x}\geqslant\mathrm{0}\:{and}\:{y}\geqslant\mathrm{0}\:\Rightarrow\mathrm{0}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}} \\ $$$$\int\int_{{D}_{{n}} \:} \:\:\:{e}^{−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} } {dxdy}\:=\int\int_{\frac{\sqrt{\mathrm{2}}}{{n}}\leqslant{r}<\sqrt{\mathrm{2}}{n}\:\:{and}\:\mathrm{0}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}}} \:\:\:{e}^{−{r}^{\mathrm{2}} } {rdr}\:{d}\theta \\ $$$$=\frac{\pi}{\mathrm{2}}\:\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left[\:{e}^{−{r}^{\mathrm{2}} } \right]_{\frac{\sqrt{\mathrm{2}}}{{n}}} ^{\sqrt{\mathrm{2}}{n}} =\frac{\pi}{\mathrm{4}}\left\{\:−{e}^{−\mathrm{2}{n}^{\mathrm{2}} } \:\:+{e}^{−\frac{\mathrm{2}}{{n}^{\mathrm{2}} }} \right\} \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:\int\int_{{D}_{{n}} } \:\:{e}^{−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} } {dxdy} \\ $$$$=\int_{\frac{\mathrm{1}}{{n}}} ^{{n}} \:{e}^{−{x}^{\mathrm{2}} } {dx}.\int_{\frac{\mathrm{1}}{{n}}} ^{{n}} \:{e}^{−{y}^{\mathrm{2}} } {dy}\:=\left(\int_{\frac{\mathrm{1}}{{n}}} ^{{n}} \:\:{e}^{−{x}^{\mathrm{2}} } {dx}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:\left(\int_{\frac{\mathrm{1}}{{n}}} ^{{n}} \:{e}^{−{x}^{\mathrm{2}} } {dx}\right)^{\mathrm{2}} \:={lim}_{{n}\rightarrow+\infty} \:{D}_{{n}} \:=\frac{\pi}{\mathrm{4}}\:\Rightarrow \\ $$$$\left(\int_{\mathrm{0}} ^{+\infty} \:{e}^{−{x}^{\mathrm{2}} } {dx}\right)^{\mathrm{2}} =\frac{\pi}{\mathrm{4}}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{x}^{\mathrm{2}} } {dx}\:=\frac{\sqrt{\pi}}{\mathrm{2}}\:. \\ $$$$ \\ $$
