
Previous in Relation and Functions Next in Relation and Functions
Question Number 99580 by mathmax by abdo last updated on 21/Jun/20
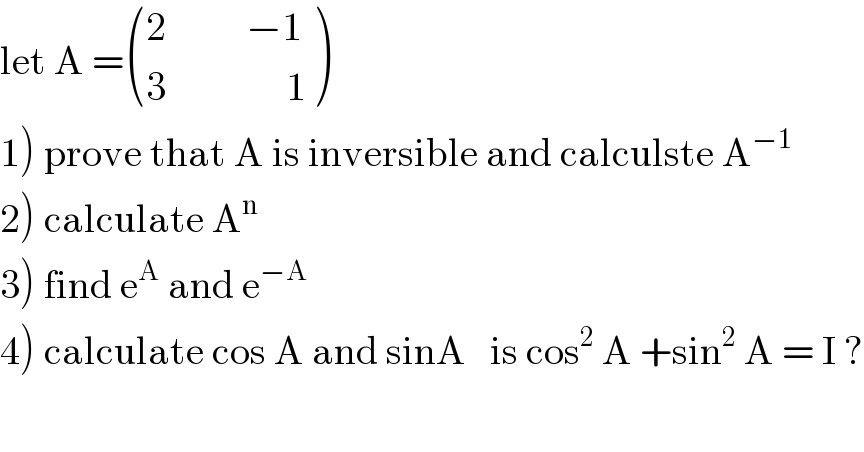
$$\mathrm{let}\:\mathrm{A}\:=\begin{pmatrix}{\mathrm{2}\:\:\:\:\:\:\:\:\:\:−\mathrm{1}}\\{\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{prove}\:\mathrm{that}\:\mathrm{A}\:\mathrm{is}\:\mathrm{inversible}\:\mathrm{and}\:\mathrm{calculste}\:\mathrm{A}^{−\mathrm{1}} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{calculate}\:\mathrm{A}^{\mathrm{n}} \\ $$$$\left.\mathrm{3}\right)\:\mathrm{find}\:\mathrm{e}^{\mathrm{A}} \:\mathrm{and}\:\mathrm{e}^{−\mathrm{A}} \\ $$$$\left.\mathrm{4}\right)\:\mathrm{calculate}\:\mathrm{cos}\:\mathrm{A}\:\mathrm{and}\:\mathrm{sinA}\:\:\:\mathrm{is}\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{A}\:+\mathrm{sin}^{\mathrm{2}} \:\mathrm{A}\:=\:\mathrm{I}\:? \\ $$$$ \\ $$
Commented by john santu last updated on 22/Jun/20
![(1) det(A) ≠ 0 ⇒A^(−1) = (1/5) [(( 1 1)),((−3 2)) ]](Q99592.png)
$$\left(\mathrm{1}\right)\:\mathrm{det}\left(\mathrm{A}\right)\:\neq\:\mathrm{0}\:\Rightarrow\mathrm{A}^{−\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{5}}\:\begin{bmatrix}{\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{1}}\\{−\mathrm{3}\:\:\:\:\:\:\mathrm{2}}\end{bmatrix} \\ $$
Answered by MWSuSon last updated on 22/Jun/20
![1) ∣A∣=2+3=5≠0 ■ 2)A^n =PD^n P^(−1) ∣A−λI∣= determinant (((2−λ),(−1)),(3,(1−λ)))=0 (2−λ)(1−λ)+3=0 λ=(1/2)(3±i(√(11))) when λ=(1/2)(3+i(√(11))) let B= ((((1/2)−i((√(11))/2)),(−1)),(3,(−(1/2)−((i(√(11)))/2))) ) BX^→ = ((((1/2)−i((√(11))/2)),(−1)),(3,(−(1/2)−((i(√(11)))/2))) ) [(x_1 ),(x_2 ) ]= [(0),(0) ] augmented matrix ((((1/2)−((i(√(11)))/2)),(−1),0),(3,(−(1/2)−((i(√(11)))/2)),0) )= [(x_1 ),(x_2 ) ] by gaussian elimination R2→R2−(3/((1/2)−((i(√(11)))/2)))R1 and R1→(2/(1−i(√(11)))) = ((1,(−(2/(1−i(√(11)))))),(0,0) ) [(x_1 ),(x_2 ) ]= [(0),(0) ] x_1 −((2x_2 )/(1−i(√(11))))=0 x_1 =((2x_2 )/(1−i(√(11)))) X^→ = [(((2ix_2 )/(i+(√(11))))),(x_2 ) ],let x_2 =1 X^→ = [(((2i)/(i+(√(11))))),(1) ] fellowing same procedure second eigenvector X^→ = [((−((2i)/((√(11))−i)))),(1) ] P= [(((2i)/((√(11))+i)),(−((2i)/((√(11))−i)))),(1,1) ] P^(−1) = [(((3i)/(√(11))),((1/2)−(i/(2(√(11)))))),((−((3i)/(√(11)))),((1/2)+(i/(2(√(11)))))) ] D=P^(−1) AP D= [(((1/2)(3+i(√(11)))),0),(0,((1/2)(3−i(√(11))))) ] Hence A^n = [(((2i)/((√(11))+i)),((2i)/(i−(√(11))))),(1,1) ] [((((1/2))^n (3+i(√(11)))^n ),0),(0,(((1/2))^n (3−(√(11)))^n )) ] [(((3i)/(√(11))),((1/2)−(i/(2(√(11)))))),((−((3i)/(√(11)))),((1/2)+(i/(2(√(11)))))) ]](Q99593.png)
$$\left.\mathrm{1}\right)\:\mid\mathrm{A}\mid=\mathrm{2}+\mathrm{3}=\mathrm{5}\neq\mathrm{0}\:\blacksquare \\ $$$$\left.\mathrm{2}\right)\mathrm{A}^{\mathrm{n}} =\mathrm{PD}^{\mathrm{n}} \mathrm{P}^{−\mathrm{1}} \\ $$$$\mid\mathrm{A}−\lambda\mathrm{I}\mid=\begin{vmatrix}{\mathrm{2}−\lambda}&{−\mathrm{1}}\\{\mathrm{3}}&{\mathrm{1}−\lambda}\end{vmatrix}=\mathrm{0} \\ $$$$\left(\mathrm{2}−\lambda\right)\left(\mathrm{1}−\lambda\right)+\mathrm{3}=\mathrm{0} \\ $$$$\lambda=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}\pm\mathrm{i}\sqrt{\mathrm{11}}\right) \\ $$$$\mathrm{when}\:\lambda=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}+\mathrm{i}\sqrt{\mathrm{11}}\right) \\ $$$$\mathrm{let}\:\mathrm{B}=\begin{pmatrix}{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{i}\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}}&{−\mathrm{1}}\\{\mathrm{3}}&{−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{i}\sqrt{\mathrm{11}}}{\mathrm{2}}}\end{pmatrix} \\ $$$$\mathrm{B}\overset{\rightarrow} {\mathrm{X}}=\begin{pmatrix}{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{i}\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}}&{−\mathrm{1}}\\{\mathrm{3}}&{−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{i}\sqrt{\mathrm{11}}}{\mathrm{2}}}\end{pmatrix}\begin{bmatrix}{\mathrm{x}_{\mathrm{1}} }\\{\mathrm{x}_{\mathrm{2}} }\end{bmatrix}=\begin{bmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{bmatrix} \\ $$$$\mathrm{augmented}\:\mathrm{matrix} \\ $$$$\begin{pmatrix}{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{i}\sqrt{\mathrm{11}}}{\mathrm{2}}}&{−\mathrm{1}}&{\mathrm{0}}\\{\mathrm{3}}&{−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{i}\sqrt{\mathrm{11}}}{\mathrm{2}}}&{\mathrm{0}}\end{pmatrix}=\begin{bmatrix}{\mathrm{x}_{\mathrm{1}} }\\{\mathrm{x}_{\mathrm{2}} }\end{bmatrix} \\ $$$$\mathrm{by}\:\mathrm{gaussian}\:\mathrm{elimination} \\ $$$$\mathrm{R2}\rightarrow\mathrm{R2}−\frac{\mathrm{3}}{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{i}\sqrt{\mathrm{11}}}{\mathrm{2}}}\mathrm{R1}\:\mathrm{and}\:\mathrm{R1}\rightarrow\frac{\mathrm{2}}{\mathrm{1}−\mathrm{i}\sqrt{\mathrm{11}}} \\ $$$$=\begin{pmatrix}{\mathrm{1}}&{−\frac{\mathrm{2}}{\mathrm{1}−\mathrm{i}\sqrt{\mathrm{11}}}}\\{\mathrm{0}}&{\mathrm{0}}\end{pmatrix}\begin{bmatrix}{\mathrm{x}_{\mathrm{1}} }\\{\mathrm{x}_{\mathrm{2}} }\end{bmatrix}=\begin{bmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{bmatrix} \\ $$$$\mathrm{x}_{\mathrm{1}} −\frac{\mathrm{2x}_{\mathrm{2}} }{\mathrm{1}−\mathrm{i}\sqrt{\mathrm{11}}}=\mathrm{0} \\ $$$$\mathrm{x}_{\mathrm{1}} =\frac{\mathrm{2x}_{\mathrm{2}} }{\mathrm{1}−\mathrm{i}\sqrt{\mathrm{11}}} \\ $$$$\overset{\rightarrow} {\mathrm{X}}=\begin{bmatrix}{\frac{\mathrm{2ix}_{\mathrm{2}} }{\mathrm{i}+\sqrt{\mathrm{11}}}}\\{\mathrm{x}_{\mathrm{2}} }\end{bmatrix},\mathrm{let}\:\mathrm{x}_{\mathrm{2}} =\mathrm{1} \\ $$$$\overset{\rightarrow} {\mathrm{X}}=\begin{bmatrix}{\frac{\mathrm{2i}}{\mathrm{i}+\sqrt{\mathrm{11}}}}\\{\mathrm{1}}\end{bmatrix} \\ $$$$\mathrm{fellowing}\:\mathrm{same}\:\mathrm{procedure}\:\mathrm{second} \\ $$$$\mathrm{eigenvector}\:\overset{\rightarrow} {\mathrm{X}}=\begin{bmatrix}{−\frac{\mathrm{2i}}{\sqrt{\mathrm{11}}−\mathrm{i}}}\\{\mathrm{1}}\end{bmatrix} \\ $$$$\mathrm{P}=\begin{bmatrix}{\frac{\mathrm{2i}}{\sqrt{\mathrm{11}}+\mathrm{i}}}&{−\frac{\mathrm{2i}}{\sqrt{\mathrm{11}}−\mathrm{i}}}\\{\mathrm{1}}&{\mathrm{1}}\end{bmatrix} \\ $$$$\mathrm{P}^{−\mathrm{1}} =\begin{bmatrix}{\frac{\mathrm{3i}}{\sqrt{\mathrm{11}}}}&{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{i}}{\mathrm{2}\sqrt{\mathrm{11}}}}\\{−\frac{\mathrm{3i}}{\sqrt{\mathrm{11}}}}&{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{i}}{\mathrm{2}\sqrt{\mathrm{11}}}}\end{bmatrix} \\ $$$$\mathrm{D}=\mathrm{P}^{−\mathrm{1}} \mathrm{AP} \\ $$$$\mathrm{D}=\begin{bmatrix}{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}+\mathrm{i}\sqrt{\mathrm{11}}\right)}&{\mathrm{0}}\\{\mathrm{0}}&{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}−\mathrm{i}\sqrt{\mathrm{11}}\right)}\end{bmatrix} \\ $$$$\mathrm{Hence}\:\mathrm{A}^{\mathrm{n}} =\begin{bmatrix}{\frac{\mathrm{2i}}{\sqrt{\mathrm{11}}+\mathrm{i}}}&{\frac{\mathrm{2i}}{\mathrm{i}−\sqrt{\mathrm{11}}}}\\{\mathrm{1}}&{\mathrm{1}}\end{bmatrix}\begin{bmatrix}{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{n}} \left(\mathrm{3}+\mathrm{i}\sqrt{\mathrm{11}}\right)^{\mathrm{n}} }&{\mathrm{0}}\\{\mathrm{0}}&{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{n}} \left(\mathrm{3}−\sqrt{\mathrm{11}}\right)^{\mathrm{n}} }\end{bmatrix}\begin{bmatrix}{\frac{\mathrm{3i}}{\sqrt{\mathrm{11}}}}&{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{i}}{\mathrm{2}\sqrt{\mathrm{11}}}}\\{−\frac{\mathrm{3i}}{\sqrt{\mathrm{11}}}}&{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{i}}{\mathrm{2}\sqrt{\mathrm{11}}}}\end{bmatrix} \\ $$$$ \\ $$
Commented by MWSuSon last updated on 22/Jun/20
you are welcome sir.
Commented by abdomathmax last updated on 22/Jun/20

$$\mathrm{thanks}\:\mathrm{sir}. \\ $$
Answered by MWSuSon last updated on 22/Jun/20
![if A= [(a_(11) ,a_(12) ),(a_(21) ,a_(22) ) ]= [(2,(−1)),(3,1) ] then e^A = [(e^a_(11) ,e^a_(12) ),(e^(a21) ,e^a_(22) ) ]= [(e^2 ,(1/e)),(e^3 ,e) ] e^(−A) = [((1/e^2 ),e),((1/e^3 ),(1/e)) ] 4)cosA= [((cos(a_(11) )),(cos(a_(12) ))),((cos(a_(21) )),(cos(a_(22) ))) ]= [((cos2),(cos1)),((cos3),(cos1)) ] sinA= [((sin2),(−sin1)),((sin3),(sin1)) ]. yes cos^2 A+sin^2 A=I](Q99594.png)
$$\mathrm{if}\:\mathrm{A}=\begin{bmatrix}{\mathrm{a}_{\mathrm{11}} }&{\mathrm{a}_{\mathrm{12}} }\\{\mathrm{a}_{\mathrm{21}} }&{\mathrm{a}_{\mathrm{22}} }\end{bmatrix}=\begin{bmatrix}{\mathrm{2}}&{−\mathrm{1}}\\{\mathrm{3}}&{\mathrm{1}}\end{bmatrix} \\ $$$$\mathrm{then}\:\mathrm{e}^{\mathrm{A}} =\begin{bmatrix}{\mathrm{e}^{\mathrm{a}_{\mathrm{11}} } }&{\mathrm{e}^{\mathrm{a}_{\mathrm{12}} } }\\{\mathrm{e}^{\mathrm{a21}} }&{\mathrm{e}^{\mathrm{a}_{\mathrm{22}} } }\end{bmatrix}=\begin{bmatrix}{\mathrm{e}^{\mathrm{2}} }&{\frac{\mathrm{1}}{\mathrm{e}}}\\{\mathrm{e}^{\mathrm{3}} }&{\mathrm{e}}\end{bmatrix} \\ $$$$\mathrm{e}^{−\mathrm{A}} =\begin{bmatrix}{\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{2}} }}&{\mathrm{e}}\\{\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{3}} }}&{\frac{\mathrm{1}}{\mathrm{e}}}\end{bmatrix} \\ $$$$\left.\mathrm{4}\right)\mathrm{cosA}=\begin{bmatrix}{\mathrm{cos}\left(\mathrm{a}_{\mathrm{11}} \right)}&{\mathrm{cos}\left(\mathrm{a}_{\mathrm{12}} \right)}\\{\mathrm{cos}\left(\mathrm{a}_{\mathrm{21}} \right)}&{\mathrm{cos}\left(\mathrm{a}_{\mathrm{22}} \right)}\end{bmatrix}=\begin{bmatrix}{\mathrm{cos2}}&{\mathrm{cos1}}\\{\mathrm{cos3}}&{\mathrm{cos1}}\end{bmatrix} \\ $$$$\mathrm{sinA}=\begin{bmatrix}{\mathrm{sin2}}&{−\mathrm{sin1}}\\{\mathrm{sin3}}&{\mathrm{sin1}}\end{bmatrix}. \\ $$$$\mathrm{yes}\:\mathrm{cos}^{\mathrm{2}} \mathrm{A}+\mathrm{sin}^{\mathrm{2}} \mathrm{A}=\mathrm{I} \\ $$
Answered by MWSuSon last updated on 22/Jun/20
![e^A =Pe^D P^(−1) e^(−A) =Pe^(−D) P^(−1) ⇒e^A = [(((2i)/((√(11))+i)),((−2i)/((√(11))−i))),(1,1) ] [(e^((1/2)(3+i(√(11)))) ,0),(0,e^((1/2)(3−i(√(11)))) ) ] [(((3i)/(√(11))),((1/2)−(i/(2(√(11)))))),((−((3i)/(√(11)))),((1/2)+(i/(2(√(11)))))) ] ⇒e^(−A) = [(((2i)/((√(11))+i)),((−2i)/((√(11))−i))),(1,1) ] [(e^(−(1/2)(3+i(√(11)))) ,0),(0,e^(−(1/2)(3−i(√(11)))) ) ] [(((3i)/(√(11))),((1/2)−(i/(2(√(11)))))),((−((3i)/(√(11)))),((1/2)+(i/(2(√(11)))))) ]](Q99597.png)
$$\mathrm{e}^{\mathrm{A}} =\mathrm{Pe}^{\mathrm{D}} \mathrm{P}^{−\mathrm{1}} \\ $$$$\mathrm{e}^{−\mathrm{A}} =\mathrm{Pe}^{−\mathrm{D}} \mathrm{P}^{−\mathrm{1}} \\ $$$$\Rightarrow\mathrm{e}^{\mathrm{A}} =\begin{bmatrix}{\frac{\mathrm{2i}}{\sqrt{\mathrm{11}}+\mathrm{i}}}&{\frac{−\mathrm{2i}}{\sqrt{\mathrm{11}}−\mathrm{i}}}\\{\mathrm{1}}&{\mathrm{1}}\end{bmatrix}\begin{bmatrix}{\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}+\mathrm{i}\sqrt{\mathrm{11}}\right)} }&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}−\mathrm{i}\sqrt{\mathrm{11}}\right)} }\end{bmatrix}\begin{bmatrix}{\frac{\mathrm{3i}}{\sqrt{\mathrm{11}}}}&{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{i}}{\mathrm{2}\sqrt{\mathrm{11}}}}\\{−\frac{\mathrm{3i}}{\sqrt{\mathrm{11}}}}&{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{i}}{\mathrm{2}\sqrt{\mathrm{11}}}}\end{bmatrix} \\ $$$$\Rightarrow\mathrm{e}^{−\mathrm{A}} =\begin{bmatrix}{\frac{\mathrm{2i}}{\sqrt{\mathrm{11}}+\mathrm{i}}}&{\frac{−\mathrm{2i}}{\sqrt{\mathrm{11}}−\mathrm{i}}}\\{\mathrm{1}}&{\mathrm{1}}\end{bmatrix}\begin{bmatrix}{\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}+\mathrm{i}\sqrt{\mathrm{11}}\right)} }&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}−\mathrm{i}\sqrt{\mathrm{11}}\right)} }\end{bmatrix}\begin{bmatrix}{\frac{\mathrm{3i}}{\sqrt{\mathrm{11}}}}&{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{i}}{\mathrm{2}\sqrt{\mathrm{11}}}}\\{−\frac{\mathrm{3i}}{\sqrt{\mathrm{11}}}}&{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{i}}{\mathrm{2}\sqrt{\mathrm{11}}}}\end{bmatrix} \\ $$
Answered by mathmax by abdo last updated on 22/Jun/20
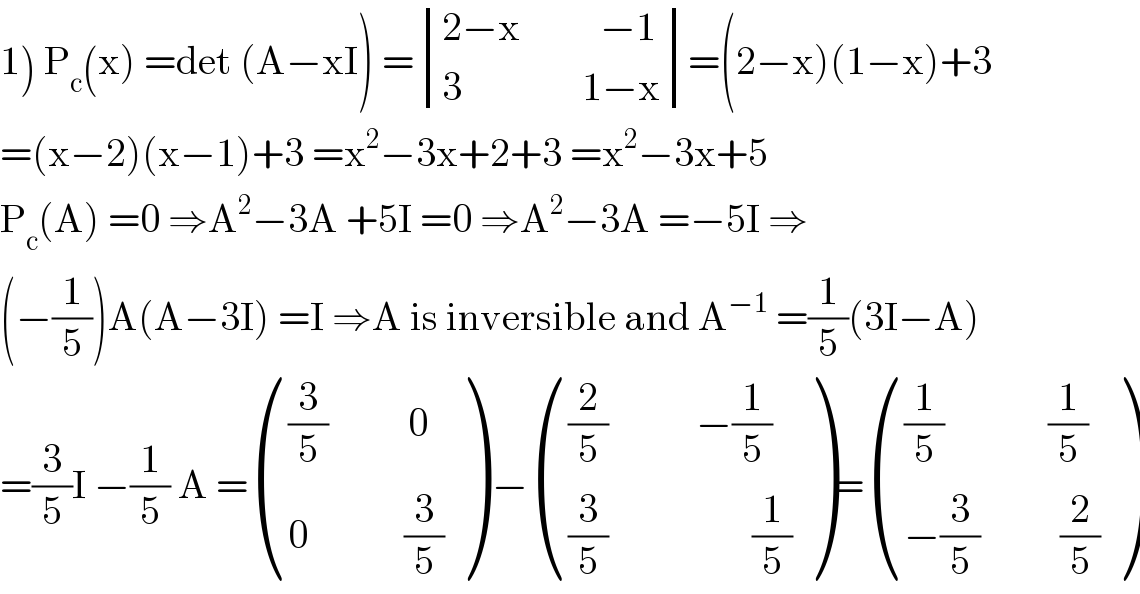
$$\left.\mathrm{1}\right)\:\mathrm{P}_{\mathrm{c}} \left(\mathrm{x}\right)\:=\mathrm{det}\:\left(\mathrm{A}−\mathrm{xI}\right)\:=\begin{vmatrix}{\mathrm{2}−\mathrm{x}\:\:\:\:\:\:\:\:\:\:−\mathrm{1}}\\{\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}−\mathrm{x}}\end{vmatrix}=\left(\mathrm{2}−\mathrm{x}\right)\left(\mathrm{1}−\mathrm{x}\right)+\mathrm{3} \\ $$$$=\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}−\mathrm{1}\right)+\mathrm{3}\:=\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{2}+\mathrm{3}\:=\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{5} \\ $$$$\mathrm{P}_{\mathrm{c}} \left(\mathrm{A}\right)\:=\mathrm{0}\:\Rightarrow\mathrm{A}^{\mathrm{2}} −\mathrm{3A}\:+\mathrm{5I}\:=\mathrm{0}\:\Rightarrow\mathrm{A}^{\mathrm{2}} −\mathrm{3A}\:=−\mathrm{5I}\:\Rightarrow \\ $$$$\left(−\frac{\mathrm{1}}{\mathrm{5}}\right)\mathrm{A}\left(\mathrm{A}−\mathrm{3I}\right)\:=\mathrm{I}\:\Rightarrow\mathrm{A}\:\mathrm{is}\:\mathrm{inversible}\:\mathrm{and}\:\mathrm{A}^{−\mathrm{1}} \:=\frac{\mathrm{1}}{\mathrm{5}}\left(\mathrm{3I}−\mathrm{A}\right) \\ $$$$=\frac{\mathrm{3}}{\mathrm{5}}\mathrm{I}\:−\frac{\mathrm{1}}{\mathrm{5}}\:\mathrm{A}\:=\begin{pmatrix}{\frac{\mathrm{3}}{\mathrm{5}}\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{3}}{\mathrm{5}}}\end{pmatrix}\:−\begin{pmatrix}{\frac{\mathrm{2}}{\mathrm{5}}\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{5}}}\\{\frac{\mathrm{3}}{\mathrm{5}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{5}}}\end{pmatrix}=\begin{pmatrix}{\frac{\mathrm{1}}{\mathrm{5}}\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{5}}}\\{−\frac{\mathrm{3}}{\mathrm{5}}\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{5}}}\end{pmatrix} \\ $$
Commented by mathmax by abdo last updated on 22/Jun/20

$$\left.\mathrm{2}\right)\:\mathrm{we}\:\mathrm{have}\:\mathrm{P}_{\mathrm{c}} \left(\mathrm{x}\right)\:=\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{5} \\ $$$$\mathrm{P}_{\mathrm{c}} \left(\mathrm{x}\right)=\mathrm{0}\:\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{5}\:=\mathrm{0}\:\:\rightarrow\Delta\:=\mathrm{9}−\mathrm{20}\:=−\mathrm{11}\:\Rightarrow\lambda_{\mathrm{1}} =\frac{\mathrm{3}+\mathrm{i}\sqrt{\mathrm{11}}}{\mathrm{2}} \\ $$$$\mathrm{and}\:\lambda_{\mathrm{2}} =\frac{\mathrm{3}−\mathrm{i}\sqrt{\mathrm{11}}}{\mathrm{2}}\:\:\:\mathrm{we}\:\mathrm{divide}\:\mathrm{x}^{\mathrm{n}} \:\mathrm{by}\:\mathrm{p}_{\mathrm{c}} \left(\mathrm{x}\right)\:\Rightarrow\mathrm{x}^{\mathrm{n}} \:=\mathrm{qp}_{\mathrm{c}} \left(\mathrm{x}\right)\:+\mathrm{u}_{\mathrm{n}} \mathrm{x}\:+\mathrm{v}_{\mathrm{n}} \\ $$$$\Rightarrow\lambda_{\mathrm{1}} ^{\mathrm{n}} \:=\mathrm{u}_{\mathrm{n}} \lambda_{\mathrm{1}} \:+\mathrm{v}_{\mathrm{n}} \:\mathrm{and}\:\lambda_{\mathrm{2}} ^{\mathrm{n}\:} \:=\mathrm{u}_{\mathrm{n}} \:\lambda_{\mathrm{2}} \:+\mathrm{v}_{\mathrm{n}} \:\Rightarrow \\ $$$$\frac{\lambda_{\mathrm{1}} ^{\mathrm{n}} −\lambda_{\mathrm{2}} ^{\mathrm{n}} }{\lambda_{\mathrm{1}} −\lambda_{\mathrm{2}} }\:=\mathrm{u}_{\mathrm{n}} \:\Rightarrow\mathrm{v}_{\mathrm{n}} =\lambda_{\mathrm{1}} ^{\mathrm{n}} −\lambda_{\mathrm{1}} \mathrm{u}_{\mathrm{n}} =\lambda_{\mathrm{1}} ^{\mathrm{n}} −\lambda_{\mathrm{1}} ×\frac{\lambda_{\mathrm{1}} ^{\mathrm{n}} \:−\lambda_{\mathrm{2}} ^{\mathrm{n}} }{\lambda_{\mathrm{1}} −\lambda_{\mathrm{2}} } \\ $$$$=\frac{\lambda_{\mathrm{1}} ^{\mathrm{n}+\mathrm{1}} −\lambda_{\mathrm{2}} \lambda_{\mathrm{1}} ^{\mathrm{n}} −\lambda_{\mathrm{1}} ^{\mathrm{n}+\mathrm{1}} \:+\lambda_{\mathrm{1}} \lambda_{\mathrm{2}} ^{\mathrm{n}} }{\lambda_{\mathrm{1}} −\lambda_{\mathrm{2}} }\:=\frac{−\mathrm{5}\:\lambda_{\mathrm{1}} ^{\mathrm{n}−\mathrm{1}} \:+\mathrm{5}\lambda_{\mathrm{2}} ^{\mathrm{n}−\mathrm{1}} }{\mathrm{i}\sqrt{\mathrm{11}}}\:=\frac{−\mathrm{5}}{\mathrm{i}\sqrt{\mathrm{11}}}\left(\lambda_{\mathrm{1}} ^{\mathrm{n}−\mathrm{1}} \:−\lambda_{\mathrm{2}} ^{\mathrm{n}−\mathrm{1}} \right) \\ $$$$\mid\lambda_{\mathrm{1}} \mid\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\sqrt{\mathrm{5}}\right)\:=\sqrt{\mathrm{5}}\:\Rightarrow\lambda_{\mathrm{1}} =\sqrt{\mathrm{5}}\mathrm{e}^{\mathrm{iarctan}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{3}}\right)} \:\mathrm{and}\:\lambda_{\mathrm{2}} =\sqrt{\mathrm{5}}\mathrm{e}^{−\mathrm{iarctan}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{3}}\right)} \:\Rightarrow \\ $$$$\mathrm{u}_{\mathrm{n}} =\frac{\left(\sqrt{\mathrm{5}}\right)^{\mathrm{n}} \:\left\{\mathrm{e}^{\mathrm{inarctan}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{3}}\right)} −\mathrm{e}^{−\mathrm{inarctan}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{3}}\right)} \right\}}{\mathrm{i}\sqrt{\mathrm{11}}}\:=\frac{\left(\sqrt{\mathrm{5}}\right)^{\mathrm{n}} }{\mathrm{i}\sqrt{\mathrm{11}}}\left\{\mathrm{2isin}\left(\mathrm{narctan}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{3}}\right)\right)\right\} \\ $$$$=\frac{\mathrm{2}\left(\sqrt{\mathrm{5}}\right)^{\mathrm{n}} }{\sqrt{\mathrm{11}}}\:\mathrm{sin}\left(\mathrm{narctan}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{3}}\right)\right) \\ $$$$\left.\mathrm{v}_{\mathrm{n}} =\frac{−\mathrm{5}}{\mathrm{i}\sqrt{\mathrm{11}}}\left\{\mathrm{2i}\:\mathrm{sin}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{arctan}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{3}}\right)\right)\right\} \\ $$$$\left.=\frac{−\mathrm{10}}{\sqrt{\mathrm{11}}}\:\left\{\mathrm{sin}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{arctan}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{3}}\right)\right)\right\} \\ $$$$\mathrm{A}^{\mathrm{n}} \:=\mathrm{u}_{\mathrm{n}} \:\mathrm{A}\:+\mathrm{v}_{\mathrm{n}} \:\mathrm{I}\:=\mathrm{u}_{\mathrm{n}} \:\begin{pmatrix}{\mathrm{2}\:\:\:\:\:\:\:\:\:−\mathrm{1}}\\{\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}\:+\mathrm{v}_{\mathrm{n}} \begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$=\begin{pmatrix}{\mathrm{2u}_{\mathrm{n}} \:+\mathrm{v}_{\mathrm{n}} \:\:\:\:\:\:\:\:\:\:−\mathrm{u}_{\mathrm{n}} }\\{\mathrm{3u}_{\mathrm{n}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{u}_{\mathrm{n}} \:+\mathrm{v}_{\mathrm{n}} }\end{pmatrix} \\ $$
