
Question Number 102576 by MAB last updated on 10/Jul/20

$${let}\:{A}_{\mathrm{1}} {A}_{\mathrm{2}} ...{A}_{{n}} \:\:{a}\:{regular}\:{polygon}\:{of}\:{n}\:{sides} \\ $$$${with}\:{length}\:{l}\:{each},\:{let}\:{X}\:{a}\:{point}\:{such} \\ $$$${that}\:{A}_{\mathrm{1}} {X}={x}\centerdot{l}\:{where}\:\mathrm{0}<{x}<\mathrm{1}\:\left({as}\:{shown}\right) \\ $$$${what}\:{is}\:{the}\:{length}\:{of}\:{the}\:{shortest}\:{path} \\ $$$${begins}\:{fromX}\:{touching}\:{all}\:{sides}\:{once} \\ $$$${and}\:{ends}\:{at}\:{X} \\ $$$$\left({there}'{s}\:{a}\:{problem}\:{shape}\:{can}'{t}\:{be}\:{loaded}\right) \\ $$
Answered by mr W last updated on 10/Jul/20
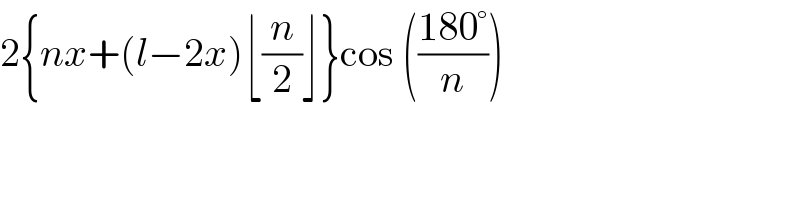
$$\mathrm{2}\left\{{nx}+\left({l}−\mathrm{2}{x}\right)\lfloor\frac{{n}}{\mathrm{2}}\rfloor\right\}\mathrm{cos}\:\left(\frac{\mathrm{180}°}{{n}}\right) \\ $$
Commented by MAB last updated on 10/Jul/20
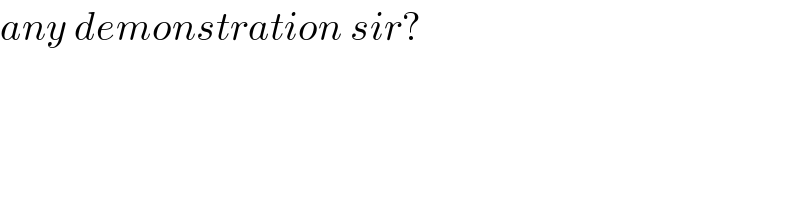
$${any}\:{demonstration}\:{sir}? \\ $$
Commented by mr W last updated on 10/Jul/20

$${answer}\:{correct}? \\ $$
Commented by MAB last updated on 10/Jul/20
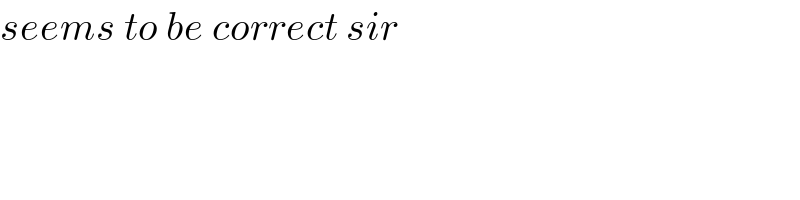
$${seems}\:{to}\:{be}\:{correct}\:{sir} \\ $$
Answered by mr W last updated on 10/Jul/20

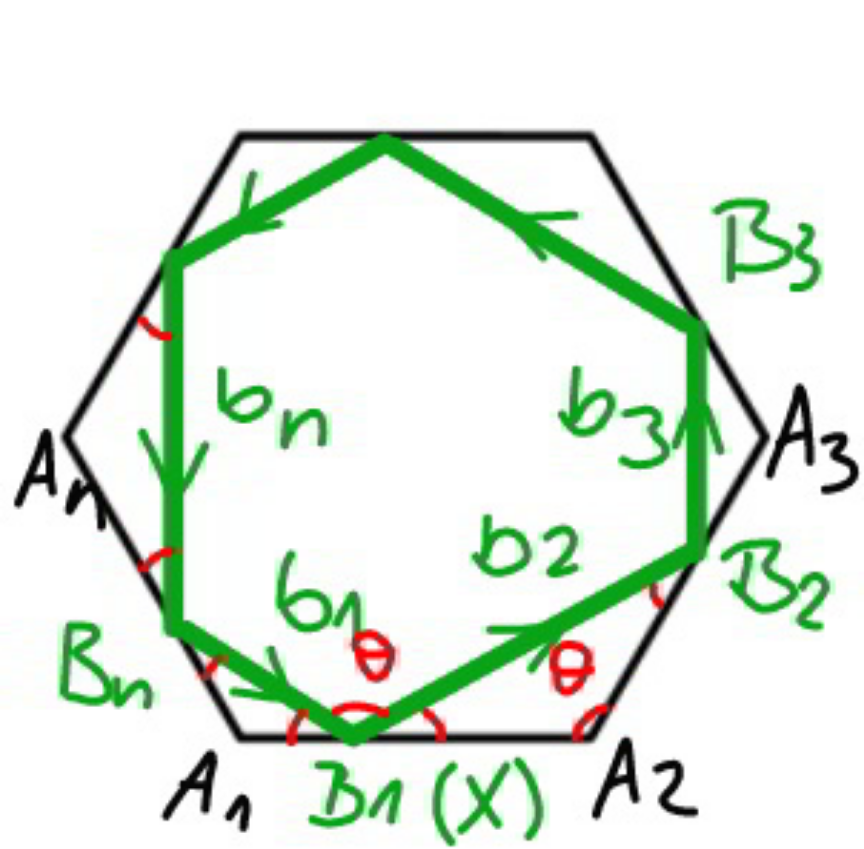
$${let}'{s}\:{say}\:{the}\:{path}\:{starts}\:{at}\:{point}\:{B}_{\mathrm{1}} \left(={X}\right) \\ $$$${and}\:{touches}\:{the}\:{other}\:{sides}\:{at}\:{points} \\ $$$${B}_{\mathrm{2}} ,{B}_{\mathrm{3}} ,...,{B}_{{n}} .\:{the}\:{path}\:{is}\:{also}\:{a}\:{n}\:{side} \\ $$$${polygon}. \\ $$$${the}\:{shortest}\:{path}\:{is}\:{that}\:{one}\:{which} \\ $$$${a}\:{light}\:{ray}\:{follows}\:{from}\:{B}_{\mathrm{1}} \:{to}\:{B}_{\mathrm{1}} \\ $$$${when}\:{reflected}\:{by}\:{all}\:{sides}\:{of}\:{the} \\ $$$${regular}\:{polygon}\:{as}\:{mirrors}. \\ $$$${if}\:{n}\:{is}\:{even},\:{we}\:{can}\:{easily}\:{see}\:{which} \\ $$$${path}\:{the}\:{light}\:{ray}\:{will}\:{follow},\:{that}'{s} \\ $$$${what}\:{the}\:{following}\:{diagram}\:{shows}. \\ $$
Commented by mr W last updated on 10/Jul/20
Commented by mr W last updated on 10/Jul/20
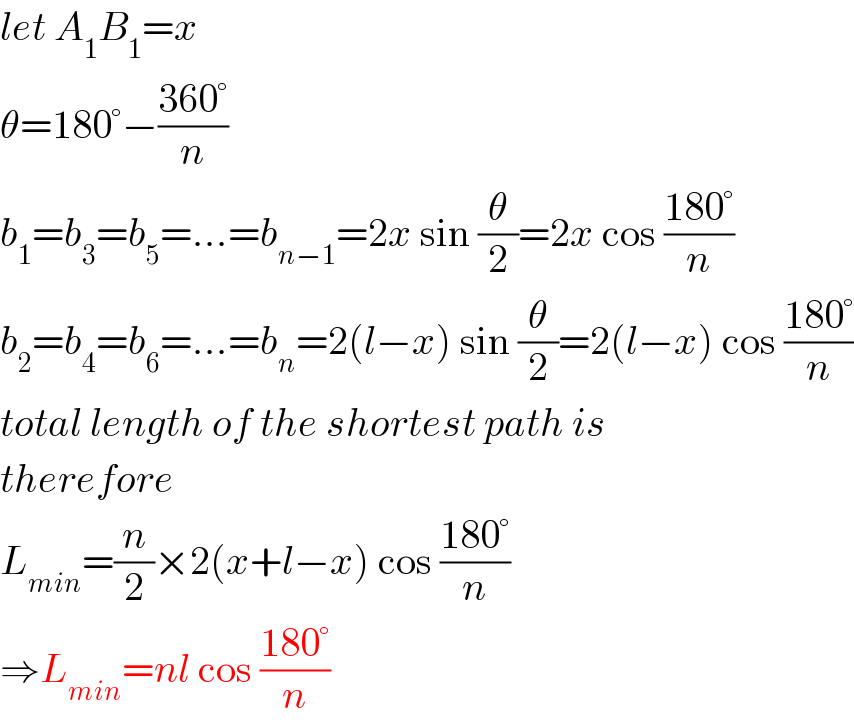
$${let}\:{A}_{\mathrm{1}} {B}_{\mathrm{1}} ={x} \\ $$$$\theta=\mathrm{180}°−\frac{\mathrm{360}°}{{n}} \\ $$$${b}_{\mathrm{1}} ={b}_{\mathrm{3}} ={b}_{\mathrm{5}} =...={b}_{{n}−\mathrm{1}} =\mathrm{2}{x}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\mathrm{2}{x}\:\mathrm{cos}\:\frac{\mathrm{180}°}{{n}} \\ $$$${b}_{\mathrm{2}} ={b}_{\mathrm{4}} ={b}_{\mathrm{6}} =...={b}_{{n}} =\mathrm{2}\left({l}−{x}\right)\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\mathrm{2}\left({l}−{x}\right)\:\mathrm{cos}\:\frac{\mathrm{180}°}{{n}} \\ $$$${total}\:{length}\:{of}\:{the}\:{shortest}\:{path}\:{is} \\ $$$${therefore} \\ $$$${L}_{{min}} =\frac{{n}}{\mathrm{2}}×\mathrm{2}\left({x}+{l}−{x}\right)\:\mathrm{cos}\:\frac{\mathrm{180}°}{{n}} \\ $$$$\Rightarrow{L}_{{min}} ={nl}\:\mathrm{cos}\:\frac{\mathrm{180}°}{{n}} \\ $$
Commented by mr W last updated on 10/Jul/20
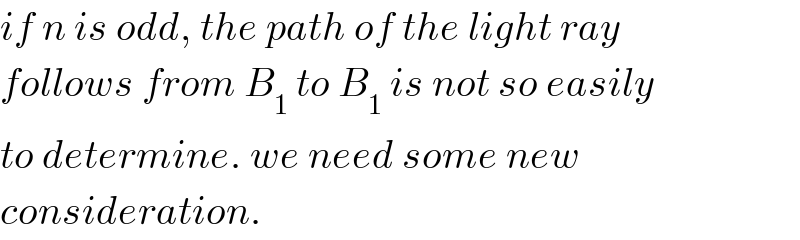
$${if}\:{n}\:{is}\:{odd},\:{the}\:{path}\:{of}\:{the}\:{light}\:{ray} \\ $$$${follows}\:{from}\:{B}_{\mathrm{1}} \:{to}\:{B}_{\mathrm{1}} \:{is}\:{not}\:{so}\:{easily} \\ $$$${to}\:{determine}.\:{we}\:{need}\:{some}\:{new} \\ $$$${consideration}. \\ $$
Commented by MAB last updated on 10/Jul/20

$${perfect}\:{sir} \\ $$
Commented by mr W last updated on 10/Jul/20
Commented by mr W last updated on 10/Jul/20
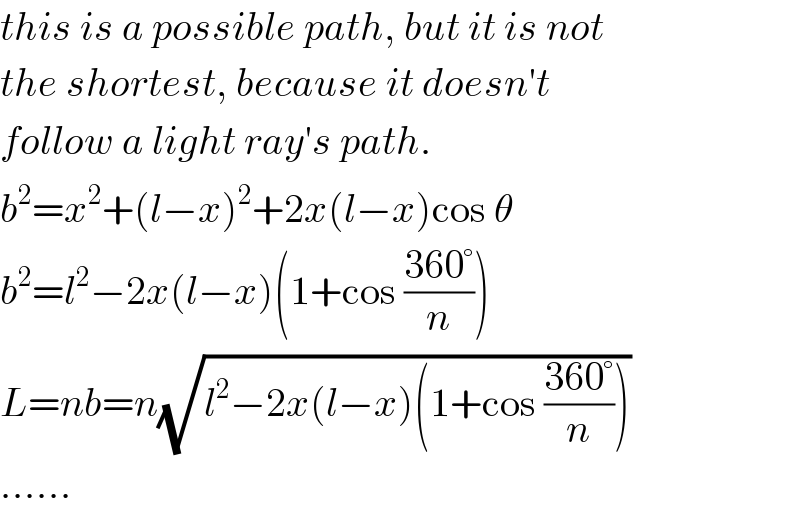
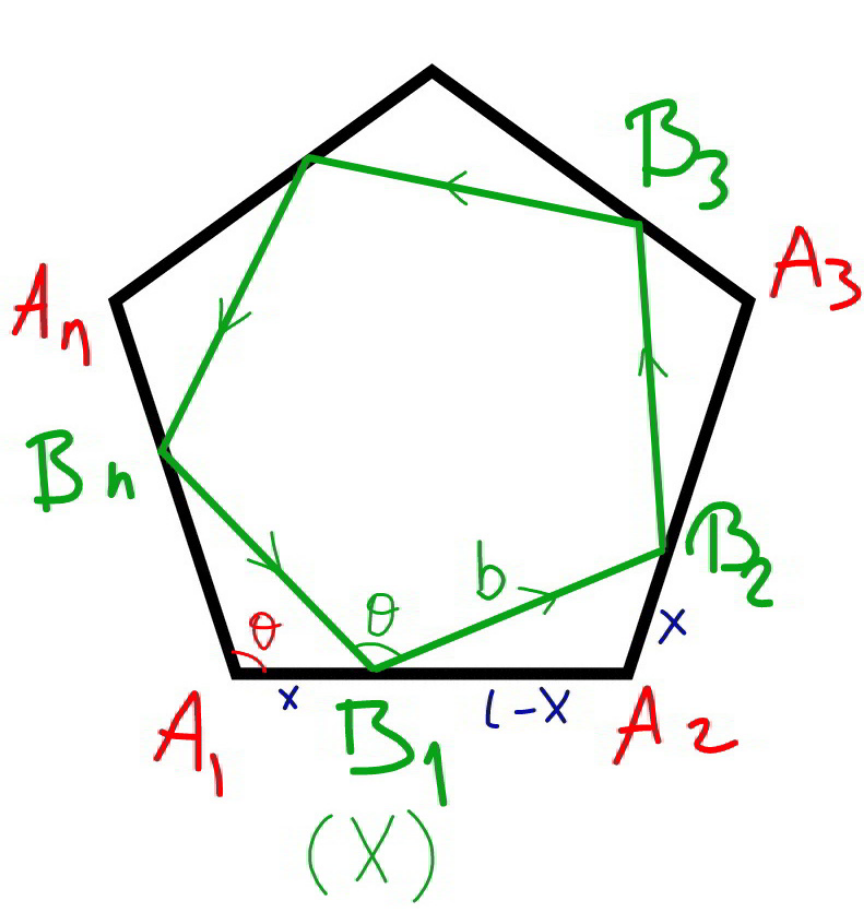
$${this}\:{is}\:{a}\:{possible}\:{path},\:{but}\:{it}\:{is}\:{not} \\ $$$${the}\:{shortest},\:{because}\:{it}\:{doesn}'{t} \\ $$$${follow}\:{a}\:{light}\:{ray}'{s}\:{path}. \\ $$$${b}^{\mathrm{2}} ={x}^{\mathrm{2}} +\left({l}−{x}\right)^{\mathrm{2}} +\mathrm{2}{x}\left({l}−{x}\right)\mathrm{cos}\:\theta \\ $$$${b}^{\mathrm{2}} ={l}^{\mathrm{2}} −\mathrm{2}{x}\left({l}−{x}\right)\left(\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{360}°}{{n}}\right) \\ $$$${L}={nb}={n}\sqrt{{l}^{\mathrm{2}} −\mathrm{2}{x}\left({l}−{x}\right)\left(\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{360}°}{{n}}\right)} \\ $$$$...... \\ $$
