Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 121919 by talminator2856791 last updated on 12/Nov/20

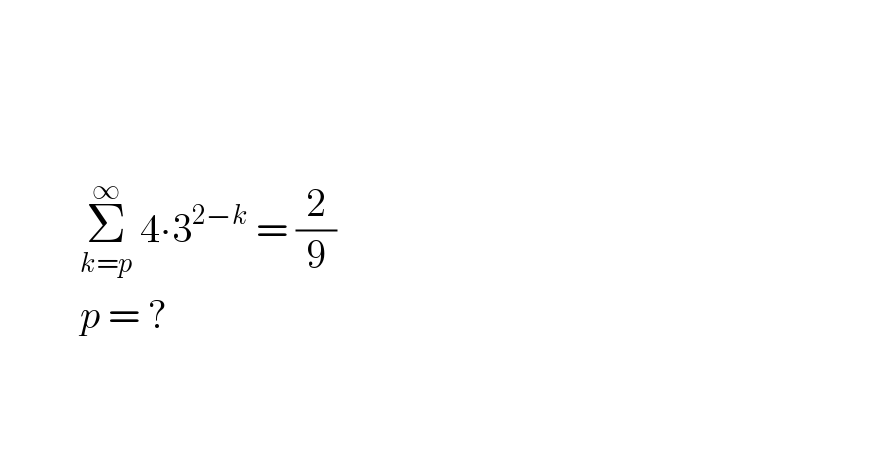
Σ_(k=p) ^∞ 4∙3^(2−k) = (2/9) p = ?

$$\: \\ $$$$\: \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\underset{{k}={p}} {\overset{\infty} {\sum}}\:\mathrm{4}\centerdot\mathrm{3}^{\mathrm{2}−{k}} \:=\:\frac{\mathrm{2}}{\mathrm{9}} \\ $$$$\:\:\:\:\:\:\:\:\:\:{p}\:=\:? \\ $$$$\: \\ $$$$\: \\ $$

Answered by Dwaipayan Shikari last updated on 12/Nov/20

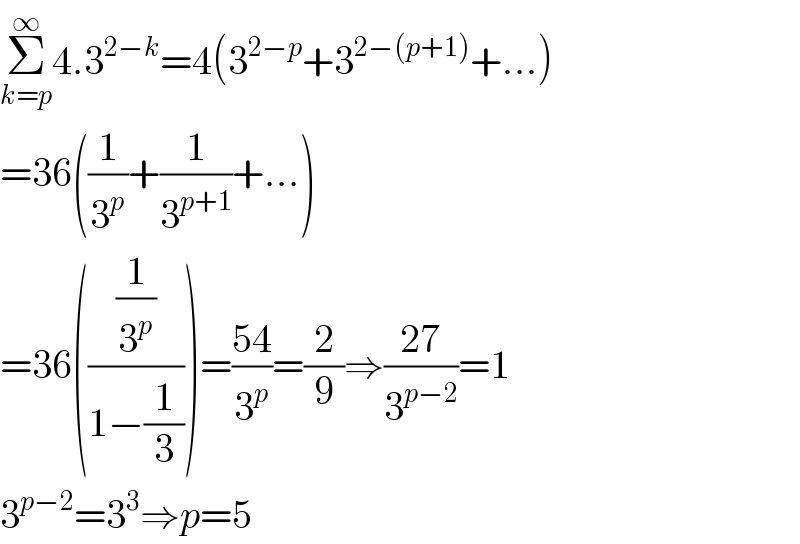
Σ_(k=p) ^∞ 4.3^(2−k) =4(3^(2−p) +3^(2−(p+1)) +...) =36((1/3^p )+(1/3^(p+1) )+...) =36(((1/3^p )/(1−(1/3))))=((54)/3^p )=(2/9)⇒((27)/3^(p−2) )=1 3^(p−2) =3^3 ⇒p=5

$$\underset{{k}={p}} {\overset{\infty} {\sum}}\mathrm{4}.\mathrm{3}^{\mathrm{2}−{k}} =\mathrm{4}\left(\mathrm{3}^{\mathrm{2}−{p}} +\mathrm{3}^{\mathrm{2}−\left({p}+\mathrm{1}\right)} +...\right) \\ $$$$=\mathrm{36}\left(\frac{\mathrm{1}}{\mathrm{3}^{{p}} }+\frac{\mathrm{1}}{\mathrm{3}^{{p}+\mathrm{1}} }+...\right) \\ $$$$=\mathrm{36}\left(\frac{\frac{\mathrm{1}}{\mathrm{3}^{{p}} }}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}}\right)=\frac{\mathrm{54}}{\mathrm{3}^{{p}} }=\frac{\mathrm{2}}{\mathrm{9}}\Rightarrow\frac{\mathrm{27}}{\mathrm{3}^{{p}−\mathrm{2}} }=\mathrm{1} \\ $$$$\mathrm{3}^{{p}−\mathrm{2}} =\mathrm{3}^{\mathrm{3}} \Rightarrow{p}=\mathrm{5} \\ $$

Answered by geoplitz last updated on 12/Nov/20

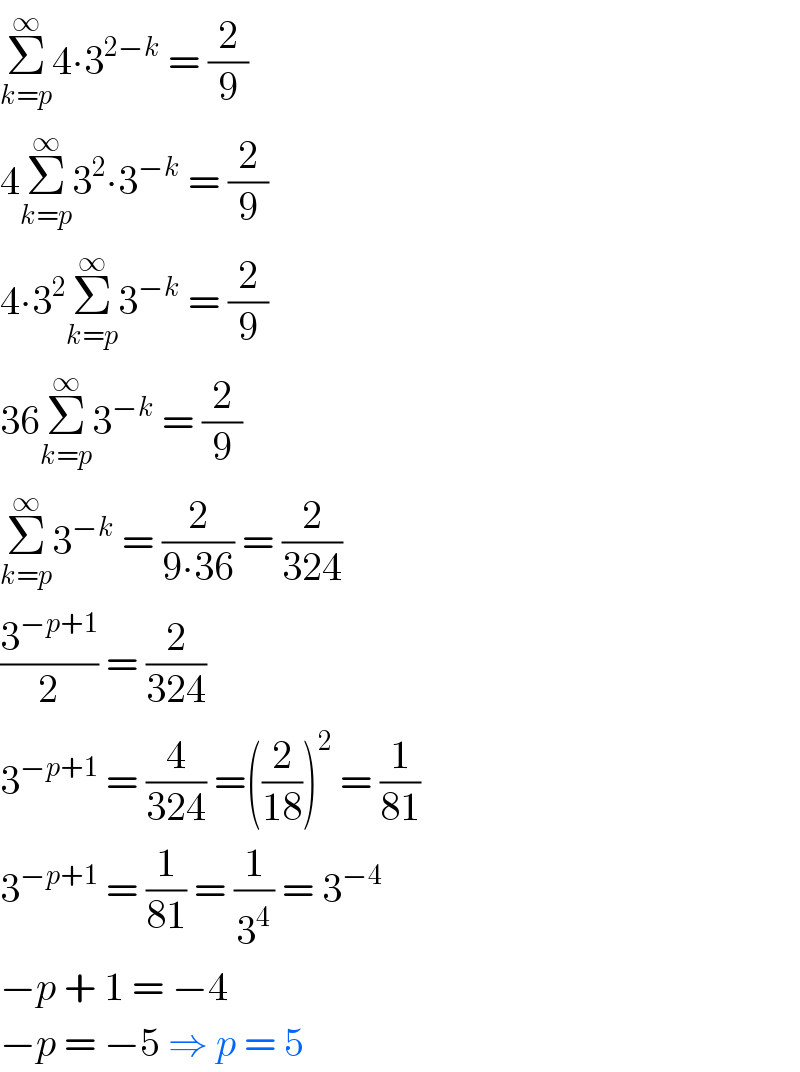
Σ_(k=p) ^∞ 4∙3^(2−k) = (2/9) 4Σ_(k=p) ^∞ 3^2 ∙3^(−k) = (2/9) 4∙3^2 Σ_(k=p) ^∞ 3^(−k) = (2/9) 36Σ_(k=p) ^∞ 3^(−k) = (2/9) Σ_(k=p) ^∞ 3^(−k) = (2/(9∙36)) = (2/(324)) (3^(−p+1) /2) = (2/(324)) 3^(−p+1) = (4/(324)) =((2/(18)))^2 = (1/(81)) 3^(−p+1) = (1/(81)) = (1/3^4 ) = 3^(−4) −p + 1 = −4 −p = −5 ⇒ p = 5

$$\underset{{k}={p}} {\overset{\infty} {\sum}}\mathrm{4}\centerdot\mathrm{3}^{\mathrm{2}−{k}} \:=\:\frac{\mathrm{2}}{\mathrm{9}} \\ $$$$\mathrm{4}\underset{{k}={p}} {\overset{\infty} {\sum}}\mathrm{3}^{\mathrm{2}} \centerdot\mathrm{3}^{−{k}} \:=\:\frac{\mathrm{2}}{\mathrm{9}} \\ $$$$\mathrm{4}\centerdot\mathrm{3}^{\mathrm{2}} \underset{{k}={p}} {\overset{\infty} {\sum}}\mathrm{3}^{−{k}} \:=\:\frac{\mathrm{2}}{\mathrm{9}} \\ $$$$\mathrm{36}\underset{{k}={p}} {\overset{\infty} {\sum}}\mathrm{3}^{−{k}} \:=\:\frac{\mathrm{2}}{\mathrm{9}} \\ $$$$\underset{{k}={p}} {\overset{\infty} {\sum}}\mathrm{3}^{−{k}} \:=\:\frac{\mathrm{2}}{\mathrm{9}\centerdot\mathrm{36}}\:=\:\frac{\mathrm{2}}{\mathrm{324}} \\ $$$$\frac{\mathrm{3}^{−{p}+\mathrm{1}} }{\mathrm{2}}\:=\:\frac{\mathrm{2}}{\mathrm{324}} \\ $$$$\mathrm{3}^{−{p}+\mathrm{1}} \:=\:\frac{\mathrm{4}}{\mathrm{324}}\:=\left(\frac{\mathrm{2}}{\mathrm{18}}\right)^{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{81}} \\ $$$$\mathrm{3}^{−{p}+\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{81}}\:=\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{4}} }\:=\:\mathrm{3}^{−\mathrm{4}} \\ $$$$−{p}\:+\:\mathrm{1}\:=\:−\mathrm{4} \\ $$$$−{p}\:=\:−\mathrm{5}\:\Rightarrow\:{p}\:=\:\mathrm{5} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com