Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 122850 by liberty last updated on 20/Nov/20

Σ_(k=1) ^n ((4k)/(4k^4 +1)) = ?

$$\:\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{\mathrm{4}{k}}{\mathrm{4}{k}^{\mathrm{4}} +\mathrm{1}}\:=\:? \\ $$

Answered by bemath last updated on 20/Nov/20

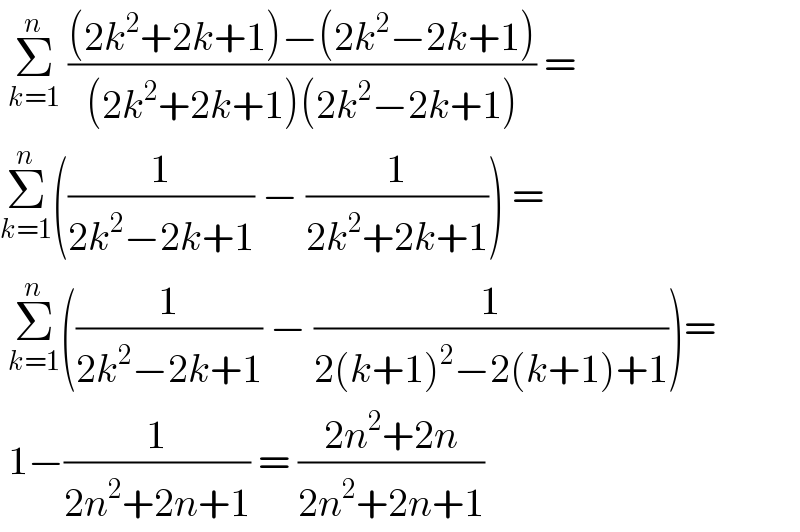
Σ_(k=1) ^n (((2k^2 +2k+1)−(2k^2 −2k+1))/((2k^2 +2k+1)(2k^2 −2k+1))) = Σ_(k=1) ^n ((1/(2k^2 −2k+1)) − (1/(2k^2 +2k+1))) = Σ_(k=1) ^n ((1/(2k^2 −2k+1)) − (1/(2(k+1)^2 −2(k+1)+1)))= 1−(1/(2n^2 +2n+1)) = ((2n^2 +2n)/(2n^2 +2n+1))

$$\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{\left(\mathrm{2}{k}^{\mathrm{2}} +\mathrm{2}{k}+\mathrm{1}\right)−\left(\mathrm{2}{k}^{\mathrm{2}} −\mathrm{2}{k}+\mathrm{1}\right)}{\left(\mathrm{2}{k}^{\mathrm{2}} +\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{2}{k}^{\mathrm{2}} −\mathrm{2}{k}+\mathrm{1}\right)}\:= \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} −\mathrm{2}{k}+\mathrm{1}}\:−\:\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} +\mathrm{2}{k}+\mathrm{1}}\right)\:= \\ $$$$\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} −\mathrm{2}{k}+\mathrm{1}}\:−\:\frac{\mathrm{1}}{\mathrm{2}\left({k}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\left({k}+\mathrm{1}\right)+\mathrm{1}}\right)= \\ $$$$\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} +\mathrm{2}{n}+\mathrm{1}}\:=\:\frac{\mathrm{2}{n}^{\mathrm{2}} +\mathrm{2}{n}}{\mathrm{2}{n}^{\mathrm{2}} +\mathrm{2}{n}+\mathrm{1}} \\ $$

Answered by Dwaipayan Shikari last updated on 20/Nov/20

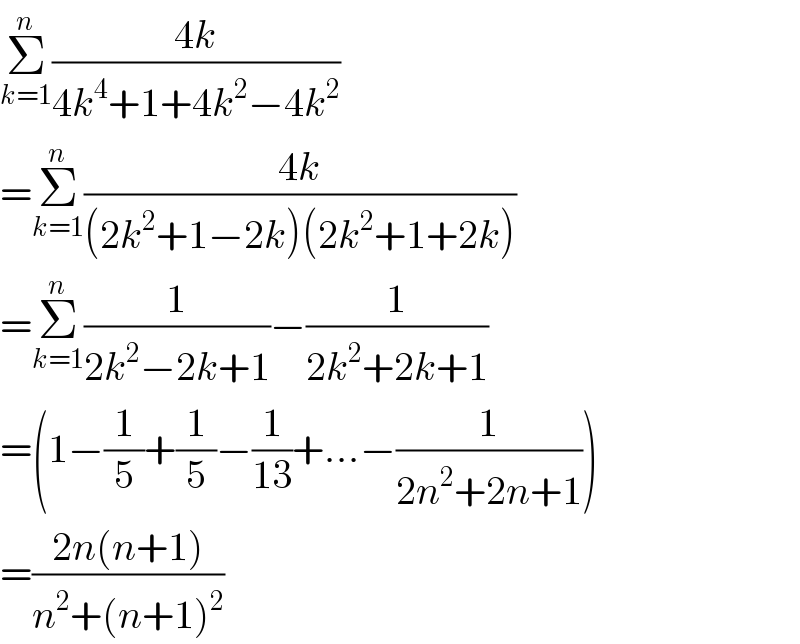
Σ_(k=1) ^n ((4k)/(4k^4 +1+4k^2 −4k^2 )) =Σ_(k=1) ^n ((4k)/((2k^2 +1−2k)(2k^2 +1+2k))) =Σ_(k=1) ^n (1/(2k^2 −2k+1))−(1/(2k^2 +2k+1)) =(1−(1/5)+(1/5)−(1/(13))+...−(1/(2n^2 +2n+1))) =((2n(n+1))/(n^2 +(n+1)^2 ))

$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{4}{k}}{\mathrm{4}{k}^{\mathrm{4}} +\mathrm{1}+\mathrm{4}{k}^{\mathrm{2}} −\mathrm{4}{k}^{\mathrm{2}} } \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{4}{k}}{\left(\mathrm{2}{k}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{k}\right)\left(\mathrm{2}{k}^{\mathrm{2}} +\mathrm{1}+\mathrm{2}{k}\right)} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} −\mathrm{2}{k}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} +\mathrm{2}{k}+\mathrm{1}} \\ $$$$=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{13}}+...−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} +\mathrm{2}{n}+\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{2}{n}\left({n}+\mathrm{1}\right)}{{n}^{\mathrm{2}} +\left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com