
Question Number 140344 by mathdave last updated on 06/May/21
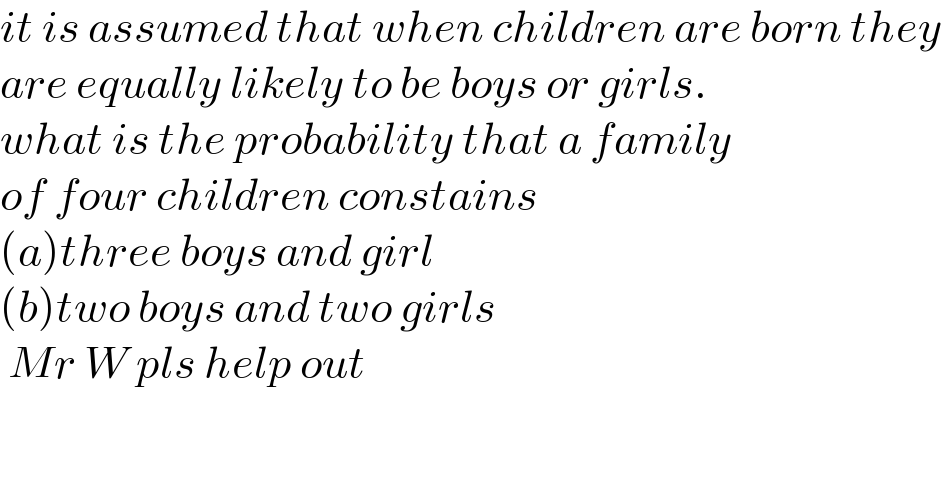
$${it}\:{is}\:{assumed}\:{that}\:{when}\:{children}\:{are}\:{born}\:{they}\: \\ $$$${are}\:{equally}\:{likely}\:{to}\:{be}\:{boys}\:{or}\:{girls}. \\ $$$${what}\:{is}\:{the}\:{probability}\:{that}\:{a}\:{family} \\ $$$${of}\:{four}\:{children}\:{constains} \\ $$$$\left({a}\right){three}\:{boys}\:{and}\:{girl} \\ $$$$\left({b}\right){two}\:{boys}\:{and}\:{two}\:{girls} \\ $$$$\:{Mr}\:{W}\:{pls}\:{help}\:{out} \\ $$
Answered by mr W last updated on 06/May/21
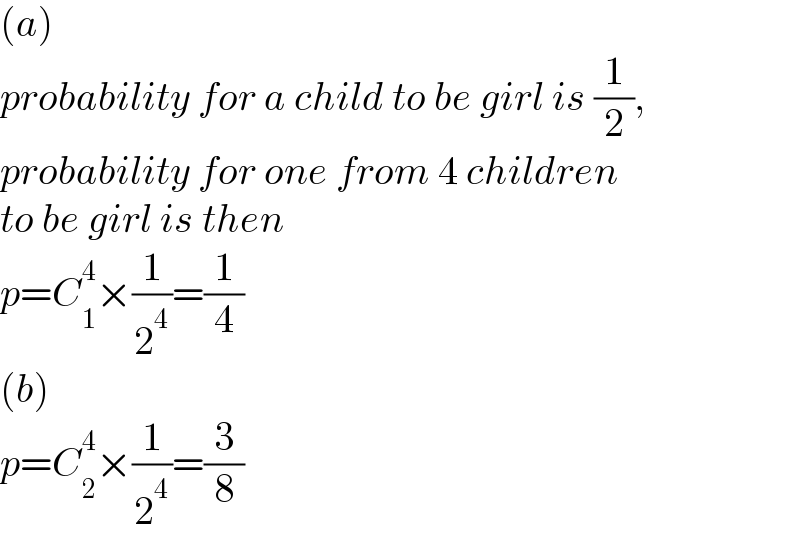
$$\left({a}\right) \\ $$$${probability}\:{for}\:{a}\:{child}\:{to}\:{be}\:{girl}\:{is}\:\frac{\mathrm{1}}{\mathrm{2}}, \\ $$$${probability}\:{for}\:{one}\:{from}\:\mathrm{4}\:{children} \\ $$$${to}\:{be}\:{girl}\:{is}\:{then} \\ $$$${p}={C}_{\mathrm{1}} ^{\mathrm{4}} ×\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\left({b}\right) \\ $$$${p}={C}_{\mathrm{2}} ^{\mathrm{4}} ×\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }=\frac{\mathrm{3}}{\mathrm{8}} \\ $$
Commented by mathdave last updated on 06/May/21
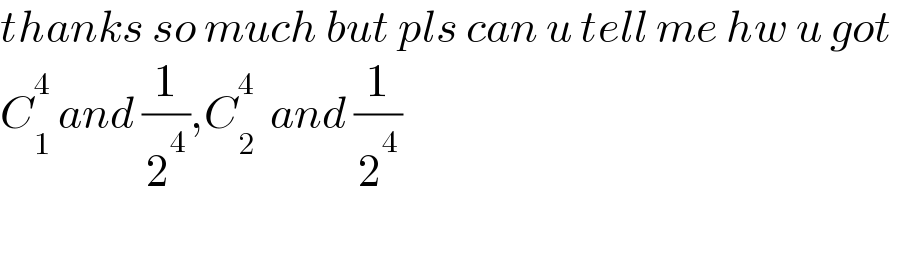
$${thanks}\:{so}\:{much}\:{but}\:{pls}\:{can}\:{u}\:{tell}\:{me}\:{hw}\:{u}\:{got}\: \\ $$$${C}_{\mathrm{1}} ^{\mathrm{4}} \:{and}\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} },{C}_{\mathrm{2}} ^{\mathrm{4}} \:\:{and}\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} } \\ $$$$ \\ $$
Commented by mr W last updated on 06/May/21
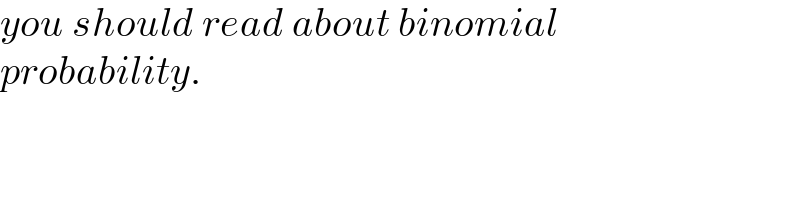
$${you}\:{should}\:{read}\:{about}\:{binomial} \\ $$$${probability}. \\ $$
Commented by mr W last updated on 06/May/21

Commented by mr W last updated on 06/May/21
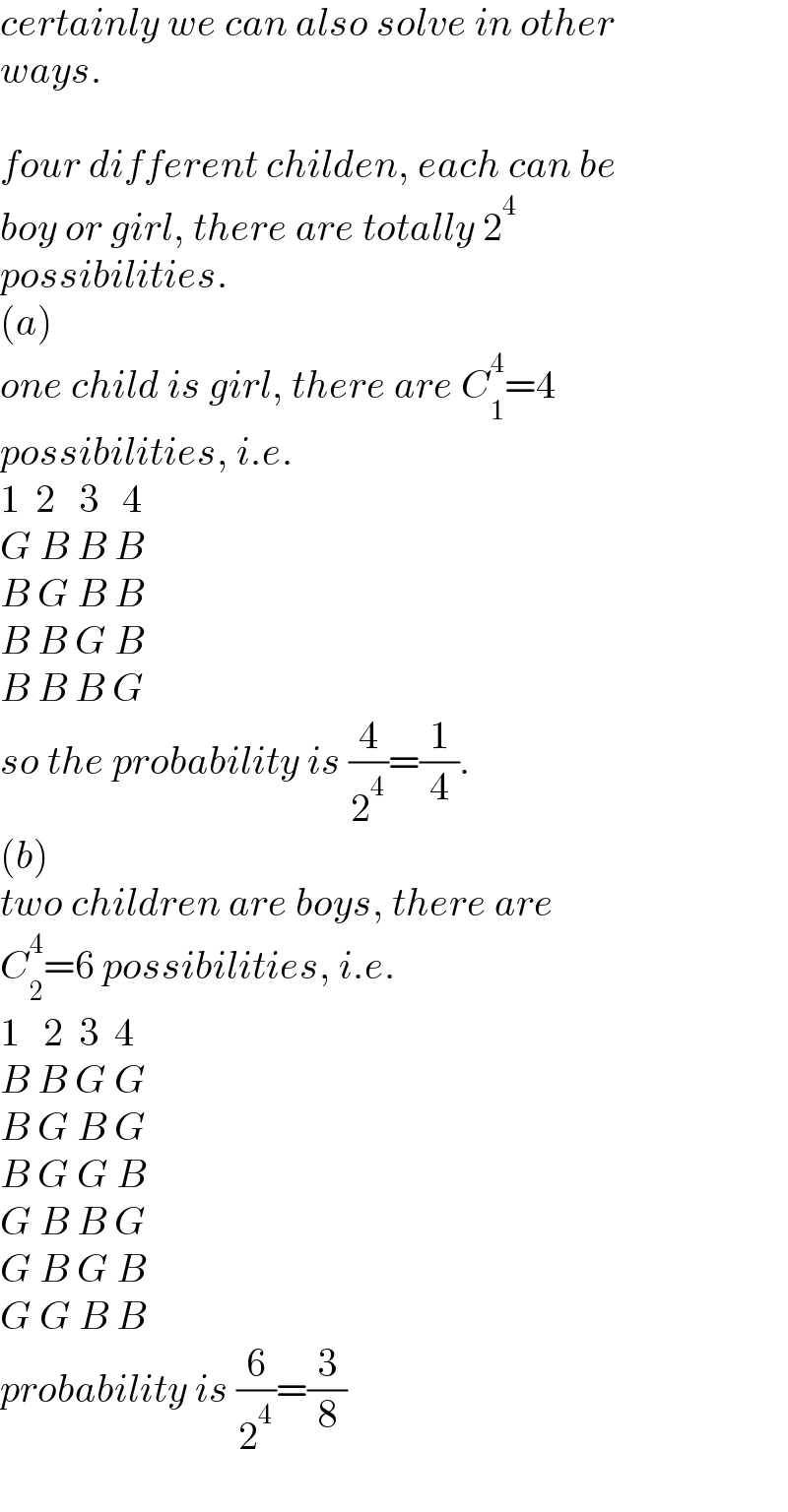
$${certainly}\:{we}\:{can}\:{also}\:{solve}\:{in}\:{other}\: \\ $$$${ways}. \\ $$$$ \\ $$$${four}\:{different}\:{childen},\:{each}\:{can}\:{be} \\ $$$${boy}\:{or}\:{girl},\:{there}\:{are}\:{totally}\:\mathrm{2}^{\mathrm{4}} \: \\ $$$${possibilities}. \\ $$$$\left({a}\right) \\ $$$${one}\:{child}\:{is}\:{girl},\:{there}\:{are}\:{C}_{\mathrm{1}} ^{\mathrm{4}} =\mathrm{4}\: \\ $$$${possibilities},\:{i}.{e}. \\ $$$$\mathrm{1}\:\:\mathrm{2}\:\:\:\mathrm{3}\:\:\:\mathrm{4} \\ $$$${G}\:{B}\:{B}\:{B} \\ $$$${B}\:{G}\:{B}\:{B} \\ $$$${B}\:{B}\:{G}\:{B} \\ $$$${B}\:{B}\:{B}\:{G} \\ $$$${so}\:{the}\:{probability}\:{is}\:\frac{\mathrm{4}}{\mathrm{2}^{\mathrm{4}} }=\frac{\mathrm{1}}{\mathrm{4}}. \\ $$$$\left({b}\right) \\ $$$${two}\:{children}\:{are}\:{boys},\:{there}\:{are} \\ $$$${C}_{\mathrm{2}} ^{\mathrm{4}} =\mathrm{6}\:{possibilities},\:{i}.{e}. \\ $$$$\mathrm{1}\:\:\:\mathrm{2}\:\:\mathrm{3}\:\:\mathrm{4} \\ $$$${B}\:{B}\:{G}\:{G} \\ $$$${B}\:{G}\:{B}\:{G} \\ $$$${B}\:{G}\:{G}\:{B} \\ $$$${G}\:{B}\:{B}\:{G} \\ $$$${G}\:{B}\:{G}\:{B} \\ $$$${G}\:{G}\:{B}\:{B} \\ $$$${probability}\:{is}\:\frac{\mathrm{6}}{\mathrm{2}^{\mathrm{4}} }=\frac{\mathrm{3}}{\mathrm{8}} \\ $$
Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
