
Question Number 206036 by Davidtim last updated on 05/Apr/24
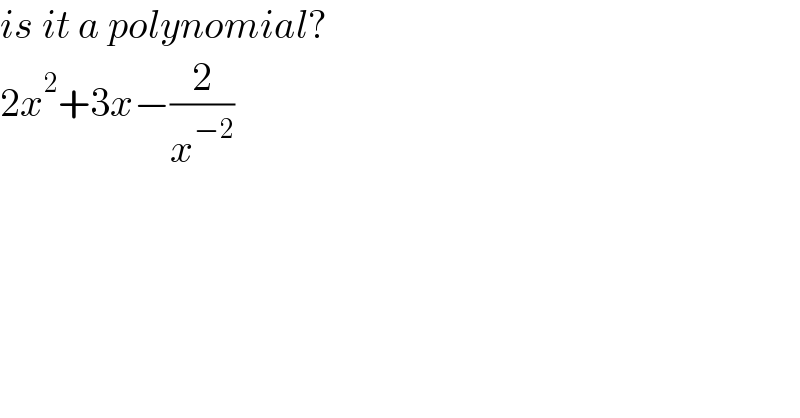
$${is}\:{it}\:{a}\:{polynomial}? \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}−\frac{\mathrm{2}}{{x}^{−\mathrm{2}} } \\ $$
Answered by Frix last updated on 05/Apr/24
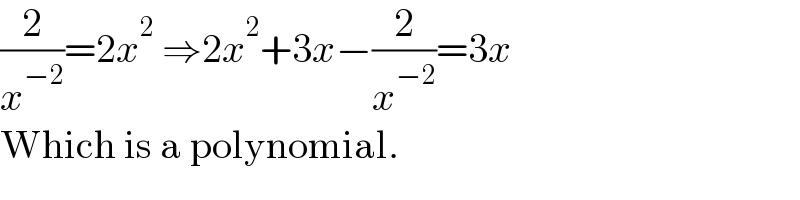
$$\frac{\mathrm{2}}{{x}^{−\mathrm{2}} }=\mathrm{2}{x}^{\mathrm{2}} \:\Rightarrow\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}−\frac{\mathrm{2}}{{x}^{−\mathrm{2}} }=\mathrm{3}{x} \\ $$$$\mathrm{Which}\:\mathrm{is}\:\mathrm{a}\:\mathrm{polynomial}. \\ $$
Commented by A5T last updated on 05/Apr/24
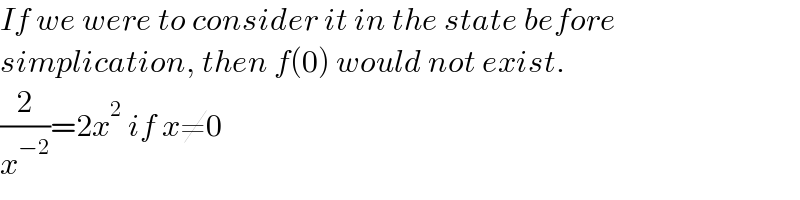
$${If}\:{we}\:{were}\:{to}\:{consider}\:{it}\:{in}\:{the}\:{state}\:{before} \\ $$$${simplication},\:{then}\:{f}\left(\mathrm{0}\right)\:{would}\:{not}\:{exist}. \\ $$$$\frac{\mathrm{2}}{{x}^{−\mathrm{2}} }=\mathrm{2}{x}^{\mathrm{2}} \:{if}\:{x}\neq\mathrm{0} \\ $$
Commented by Frix last updated on 05/Apr/24

$$\mathrm{You}'\mathrm{re}\:\mathrm{right}. \\ $$
