
Question Number 30419 by abdo imad last updated on 22/Feb/18
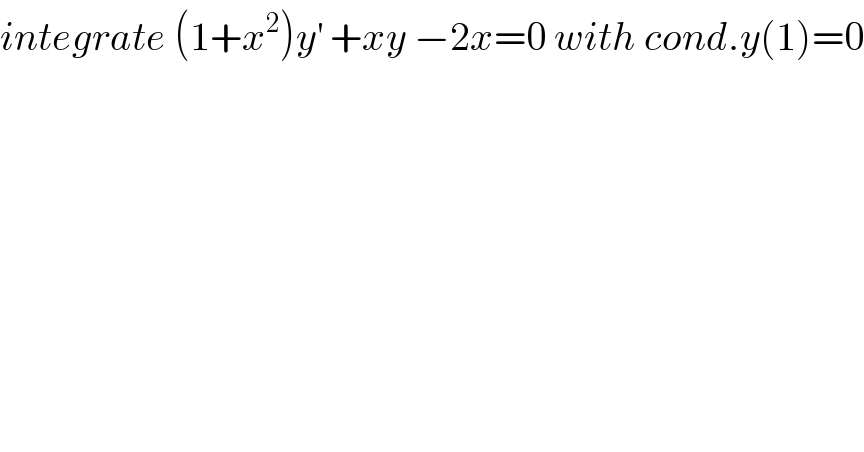
$${integrate}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}^{'} \:+{xy}\:−\mathrm{2}{x}=\mathrm{0}\:{with}\:{cond}.{y}\left(\mathrm{1}\right)=\mathrm{0} \\ $$
Answered by sma3l2996 last updated on 24/Feb/18
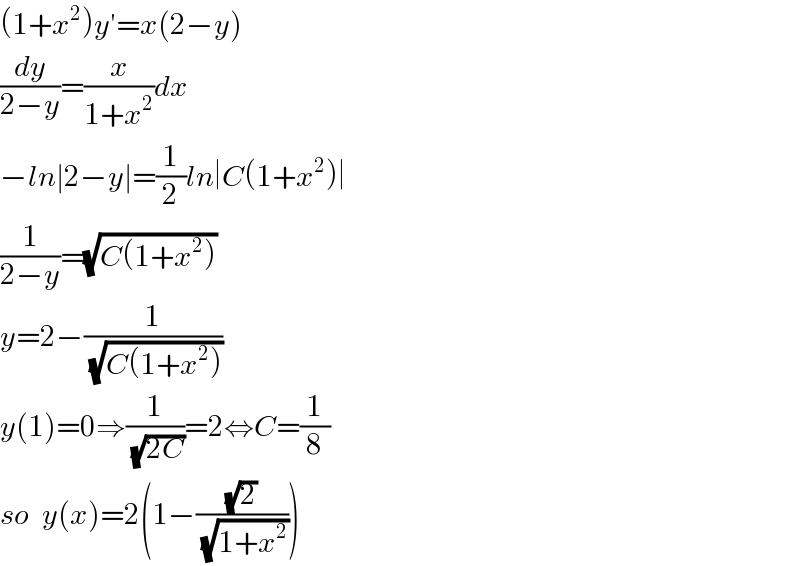
$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}'={x}\left(\mathrm{2}−{y}\right) \\ $$$$\frac{{dy}}{\mathrm{2}−{y}}=\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$−{ln}\mid\mathrm{2}−{y}\mid=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{C}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\mid \\ $$$$\frac{\mathrm{1}}{\mathrm{2}−{y}}=\sqrt{{C}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$$${y}=\mathrm{2}−\frac{\mathrm{1}}{\sqrt{{C}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}} \\ $$$${y}\left(\mathrm{1}\right)=\mathrm{0}\Rightarrow\frac{\mathrm{1}}{\sqrt{\mathrm{2}{C}}}=\mathrm{2}\Leftrightarrow{C}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$${so}\:\:{y}\left({x}\right)=\mathrm{2}\left(\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right) \\ $$
