
Question Number 204707 by Mummyjay last updated on 25/Feb/24
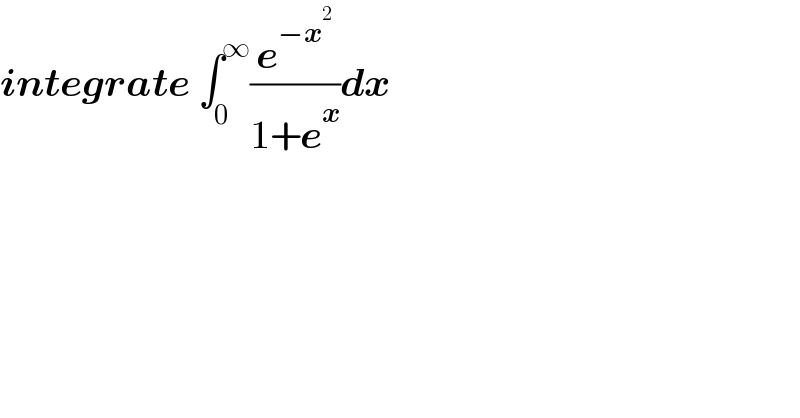
$$\boldsymbol{{integrate}}\:\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{e}}^{−\boldsymbol{{x}}^{\mathrm{2}} } }{\mathrm{1}+\boldsymbol{{e}}^{\boldsymbol{{x}}} }\boldsymbol{{dx}} \\ $$
Answered by witcher3 last updated on 26/Feb/24
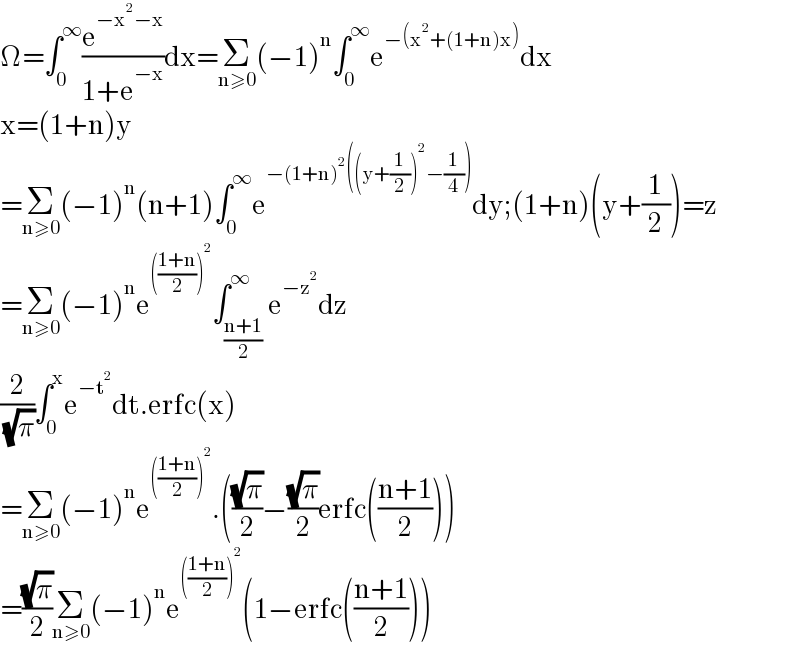
$$\Omega=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} −\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{x}} }\mathrm{dx}=\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{\mathrm{n}} \int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\left(\mathrm{x}^{\mathrm{2}} +\left(\mathrm{1}+\mathrm{n}\right)\mathrm{x}\right)} \mathrm{dx} \\ $$$$\mathrm{x}=\left(\mathrm{1}+\mathrm{n}\right)\mathrm{y} \\ $$$$=\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{n}+\mathrm{1}\right)\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\left(\mathrm{1}+\mathrm{n}\right)^{\mathrm{2}} \left(\left(\mathrm{y}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\right)} \mathrm{dy};\left(\mathrm{1}+\mathrm{n}\right)\left(\mathrm{y}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{z} \\ $$$$=\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{e}^{\left(\frac{\mathrm{1}+\mathrm{n}}{\mathrm{2}}\right)^{\mathrm{2}} } \int_{\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}}} ^{\infty} \mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz} \\ $$$$\frac{\mathrm{2}}{\:\sqrt{\pi}}\int_{\mathrm{0}} ^{\mathrm{x}} \mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{dt}.\mathrm{erfc}\left(\mathrm{x}\right) \\ $$$$=\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{e}^{\left(\frac{\mathrm{1}+\mathrm{n}}{\mathrm{2}}\right)^{\mathrm{2}} } .\left(\frac{\sqrt{\pi}}{\mathrm{2}}−\frac{\sqrt{\pi}}{\mathrm{2}}\mathrm{erfc}\left(\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}}\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{e}^{\left(\frac{\mathrm{1}+\mathrm{n}}{\mathrm{2}}\right)^{\mathrm{2}} } \left(\mathrm{1}−\mathrm{erfc}\left(\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$
