
Question Number 175585 by mnjuly1970 last updated on 03/Sep/22
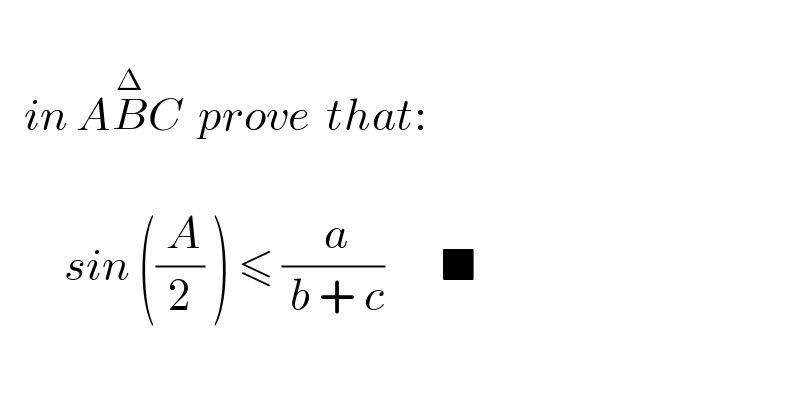
$$ \\ $$$$\:\:\:{in}\:{A}\overset{\Delta} {{B}C}\:\:{prove}\:\:{that}: \\ $$$$\:\:\: \\ $$$$\:\:\:\:\:\:\:\:{sin}\:\left(\frac{\:{A}}{\mathrm{2}}\:\right)\:\leqslant\:\frac{\:{a}}{\:{b}\:+\:{c}}\:\:\:\:\:\:\:\blacksquare \\ $$$$ \\ $$
Commented by mahdipoor last updated on 05/Sep/22
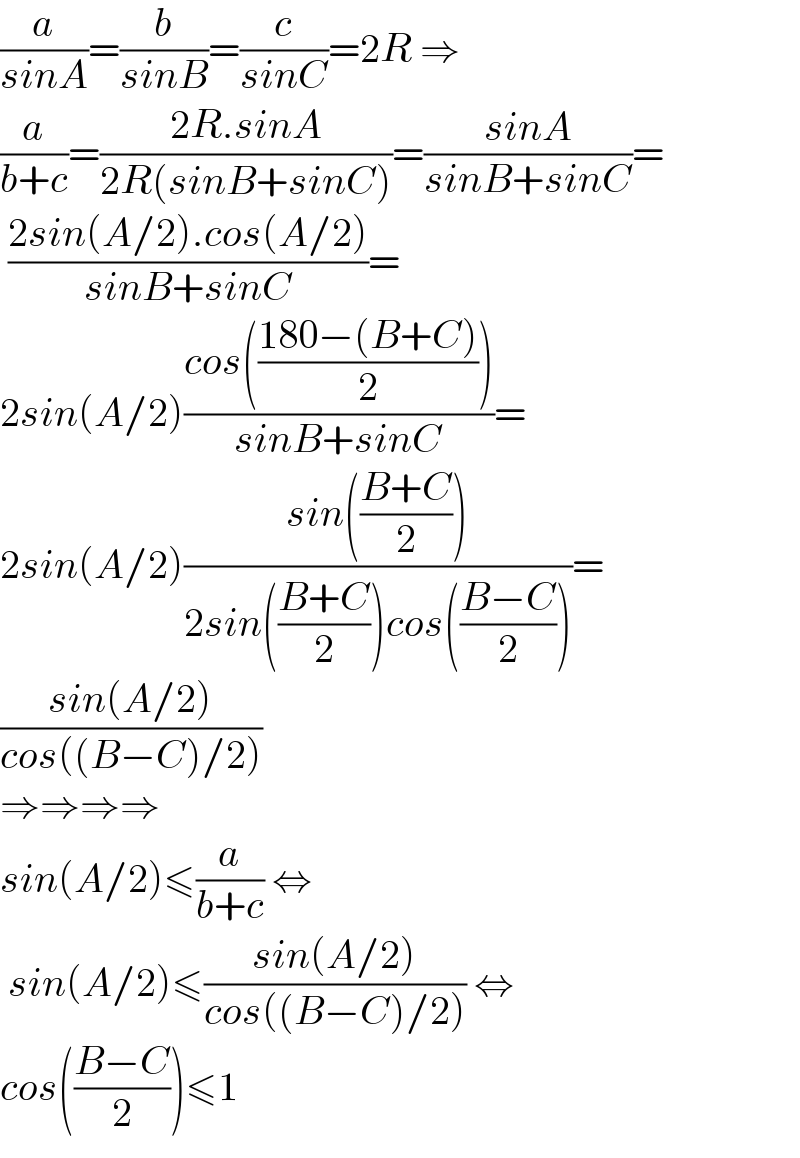
$$\frac{{a}}{{sinA}}=\frac{{b}}{{sinB}}=\frac{{c}}{{sinC}}=\mathrm{2}{R}\:\Rightarrow \\ $$$$\frac{{a}}{{b}+{c}}=\frac{\mathrm{2}{R}.{sinA}}{\mathrm{2}{R}\left({sinB}+{sinC}\right)}=\frac{{sinA}}{{sinB}+{sinC}}= \\ $$$$\:\frac{\mathrm{2}{sin}\left({A}/\mathrm{2}\right).{cos}\left({A}/\mathrm{2}\right)}{{sinB}+{sinC}}= \\ $$$$\mathrm{2}{sin}\left({A}/\mathrm{2}\right)\frac{{cos}\left(\frac{\mathrm{180}−\left({B}+{C}\right)}{\mathrm{2}}\right)}{{sinB}+{sinC}}= \\ $$$$\mathrm{2}{sin}\left({A}/\mathrm{2}\right)\frac{{sin}\left(\frac{{B}+{C}}{\mathrm{2}}\right)}{\mathrm{2}{sin}\left(\frac{{B}+{C}}{\mathrm{2}}\right){cos}\left(\frac{{B}−{C}}{\mathrm{2}}\right)}= \\ $$$$\frac{{sin}\left({A}/\mathrm{2}\right)}{{cos}\left(\left({B}−{C}\right)/\mathrm{2}\right)} \\ $$$$\Rightarrow\Rightarrow\Rightarrow\Rightarrow \\ $$$${sin}\left({A}/\mathrm{2}\right)\leqslant\frac{{a}}{{b}+{c}}\:\Leftrightarrow \\ $$$$\:{sin}\left({A}/\mathrm{2}\right)\leqslant\frac{{sin}\left({A}/\mathrm{2}\right)}{{cos}\left(\left({B}−{C}\right)/\mathrm{2}\right)}\:\Leftrightarrow \\ $$$${cos}\left(\frac{{B}−{C}}{\mathrm{2}}\right)\leqslant\mathrm{1}\: \\ $$
Commented by mnjuly1970 last updated on 03/Sep/22

$${zendeh}\:{bashid}\:{ostad}\:{mahdipoor}\: \\ $$$${mamnoon}.{besiar}\:{ali}\:{bood}. \\ $$
Commented by mahdipoor last updated on 03/Sep/22

$$\heartsuit \\ $$
Commented by behi834171 last updated on 03/Sep/22
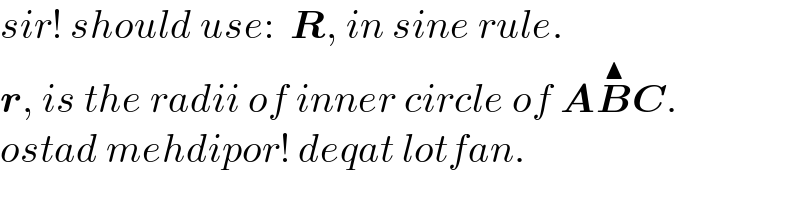
$${sir}!\:{should}\:{use}:\:\:\boldsymbol{{R}},\:{in}\:{sine}\:{rule}. \\ $$$$\boldsymbol{{r}},\:{is}\:{the}\:{radii}\:{of}\:{inner}\:{circle}\:{of}\:\boldsymbol{{A}}\overset{\blacktriangle} {\boldsymbol{{B}C}}. \\ $$$${ostad}\:{mehdipor}!\:{deqat}\:{lotfan}. \\ $$
Commented by mnjuly1970 last updated on 04/Sep/22

$$\:\:{eradatmandim}\:{ostad}\:.. \\ $$
Commented by mahdipoor last updated on 05/Sep/22
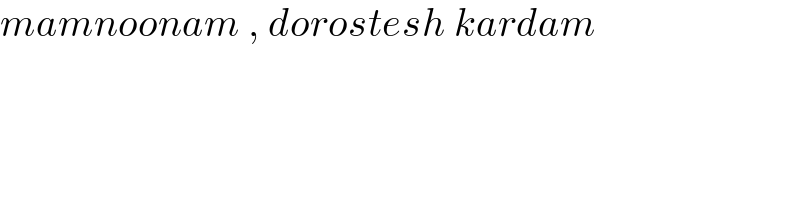
$${mamnoonam}\:,\:{dorostesh}\:{kardam} \\ $$
Answered by behi834171 last updated on 03/Sep/22
![sin(A/2)=(√(((p−b)(p−c))/(bc)))⇒ (√(((p−b)(p−c))/(bc)))≤(a/(b+c))⇒ ((√(p(p−a)(p−b)(p−c)))/( (√(p(p−a).abc))))≤((√a)/(b+c))⇒ (S/( (√(p(p−a)4R.S))))≤((√a)/(b+c))⇒((√r)/(2(√((p−a)R))))≤((√a)/(b+c))⇒ ⇒(√(r/R))≤((2(√(a(p−a))))/(b+c))⇒(r/R)≤((4a(p−a))/((b+c)^2 )) ((4a(p−a))/((b+c)^2 ))=((2a(b+c−a))/((b+c)^2 ))=2(a/(b+c))−2((a/(b+c)))^2 =2t−2t^2 f(t)=2t−2t^2 ⇒(df/dt)=2(1−2t)=0⇒t=(1/2) f_(min) =2×(1/2)−2×(1/4)=1−(1/2)=(1/2)⇒f≤(1/2)⇒ ⇒(r/R)≤(1/2)⇒R≥2r .this is true. [Euler′s rule: d^2 =R^2 −2R.r=R(R−2r)≥0⇒R≥2r]](Q175611.png)
$${sin}\frac{{A}}{\mathrm{2}}=\sqrt{\frac{\left({p}−{b}\right)\left({p}−{c}\right)}{{bc}}}\Rightarrow \\ $$$$\sqrt{\frac{\left({p}−{b}\right)\left({p}−{c}\right)}{{bc}}}\leqslant\frac{{a}}{{b}+{c}}\Rightarrow \\ $$$$\frac{\sqrt{{p}\left({p}−{a}\right)\left({p}−{b}\right)\left({p}−{c}\right)}}{\:\sqrt{{p}\left({p}−{a}\right).{abc}}}\leqslant\frac{\sqrt{{a}}}{{b}+{c}}\Rightarrow \\ $$$$\frac{{S}}{\:\sqrt{{p}\left({p}−{a}\right)\mathrm{4}{R}.{S}}}\leqslant\frac{\sqrt{{a}}}{{b}+{c}}\Rightarrow\frac{\sqrt{{r}}}{\mathrm{2}\sqrt{\left({p}−{a}\right){R}}}\leqslant\frac{\sqrt{{a}}}{{b}+{c}}\Rightarrow \\ $$$$\Rightarrow\sqrt{\frac{\boldsymbol{{r}}}{\boldsymbol{{R}}}}\leqslant\frac{\mathrm{2}\sqrt{\boldsymbol{{a}}\left(\boldsymbol{{p}}−\boldsymbol{{a}}\right)}}{\boldsymbol{{b}}+\boldsymbol{{c}}}\Rightarrow\frac{\boldsymbol{{r}}}{\boldsymbol{{R}}}\leqslant\frac{\mathrm{4}\boldsymbol{{a}}\left(\boldsymbol{{p}}−\boldsymbol{{a}}\right)}{\left(\boldsymbol{{b}}+\boldsymbol{{c}}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{4}\boldsymbol{{a}}\left(\boldsymbol{{p}}−\boldsymbol{{a}}\right)}{\left(\boldsymbol{{b}}+\boldsymbol{{c}}\right)^{\mathrm{2}} }=\frac{\mathrm{2}\boldsymbol{{a}}\left(\boldsymbol{{b}}+\boldsymbol{{c}}−\boldsymbol{{a}}\right)}{\left(\boldsymbol{{b}}+\boldsymbol{{c}}\right)^{\mathrm{2}} }=\mathrm{2}\frac{\boldsymbol{{a}}}{\boldsymbol{{b}}+\boldsymbol{{c}}}−\mathrm{2}\left(\frac{\boldsymbol{{a}}}{\boldsymbol{{b}}+\boldsymbol{{c}}}\right)^{\mathrm{2}} \\ $$$$=\mathrm{2}\boldsymbol{{t}}−\mathrm{2}\boldsymbol{{t}}^{\mathrm{2}} \\ $$$$\boldsymbol{{f}}\left(\boldsymbol{{t}}\right)=\mathrm{2}\boldsymbol{{t}}−\mathrm{2}\boldsymbol{{t}}^{\mathrm{2}} \Rightarrow\frac{\boldsymbol{{df}}}{\boldsymbol{{dt}}}=\mathrm{2}\left(\mathrm{1}−\mathrm{2}\boldsymbol{{t}}\right)=\mathrm{0}\Rightarrow\boldsymbol{{t}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\boldsymbol{{f}}_{\boldsymbol{{min}}} =\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\boldsymbol{{f}}\leqslant\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow \\ $$$$\Rightarrow\frac{\boldsymbol{{r}}}{\boldsymbol{{R}}}\leqslant\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\boldsymbol{{R}}\geqslant\mathrm{2}\boldsymbol{{r}}\:\:.\boldsymbol{{this}}\:\boldsymbol{{is}}\:\boldsymbol{{true}}. \\ $$$$\left[\boldsymbol{{Euler}}'\boldsymbol{{s}}\:\boldsymbol{{rule}}:\right. \\ $$$$\left.\boldsymbol{{d}}^{\mathrm{2}} =\boldsymbol{{R}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{R}}.\boldsymbol{{r}}=\boldsymbol{{R}}\left(\boldsymbol{{R}}−\mathrm{2}\boldsymbol{{r}}\right)\geqslant\mathrm{0}\Rightarrow\boldsymbol{{R}}\geqslant\mathrm{2}\boldsymbol{{r}}\right] \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 04/Sep/22
$$\:\:{zendeh}\:{bashid}\:{ostad}\:{bozorgvar} \\ $$$${kheili}\:{ali}\:{bood}. \\ $$
Commented by behi834171 last updated on 04/Sep/22
$${mamnon}.{shoma}\:{ham}\:{binazir}\:{hasted}. \\ $$$${zende}\:{bashid}. \\ $$
