Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 188515 by mnjuly1970 last updated on 02/Mar/23

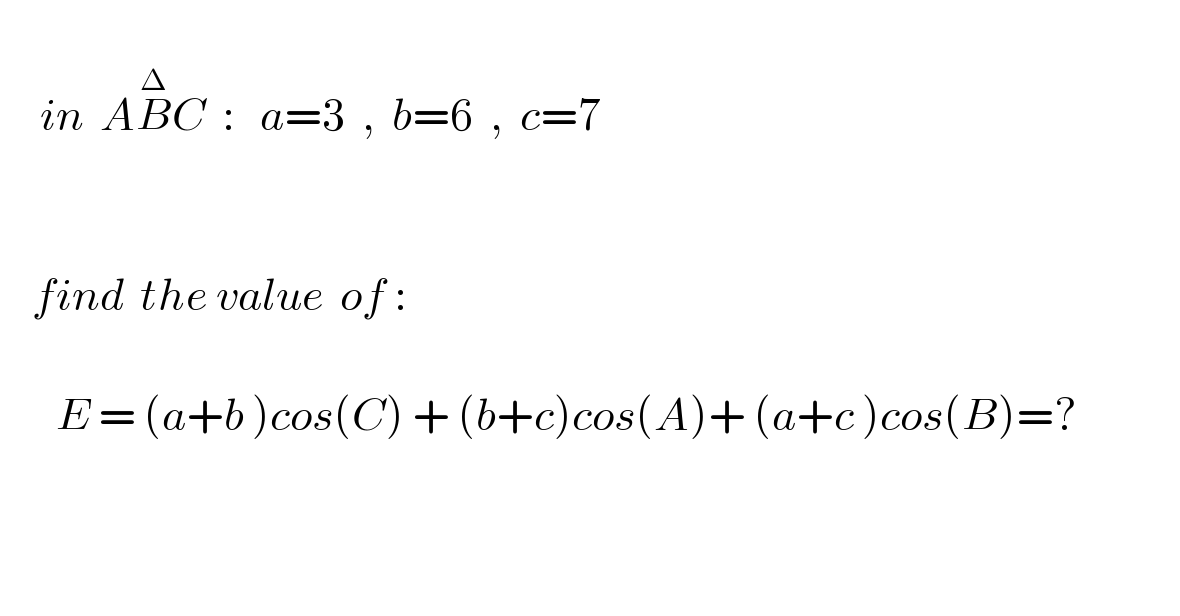
in AB^Δ C : a=3 , b=6 , c=7 find the value of : E = (a+b )cos(C) + (b+c)cos(A)+ (a+c )cos(B)=?

$$ \\ $$$$\:\:\:\:\:{in}\:\:{A}\overset{\Delta} {{B}C}\:\::\:\:\:{a}=\mathrm{3}\:\:,\:\:{b}=\mathrm{6}\:\:,\:\:{c}=\mathrm{7} \\ $$$$\:\:\: \\ $$$$\: \\ $$$$\:\:\:\:{find}\:\:{the}\:{value}\:\:{of}\:: \\ $$$$\:\:\: \\ $$$$\:\:\:\:\:\:\:{E}\:=\:\left({a}+{b}\:\right){cos}\left({C}\right)\:+\:\left({b}+{c}\right){cos}\left({A}\right)+\:\left({a}+{c}\:\right){cos}\left({B}\right)=?\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\: \\ $$

Answered by mr W last updated on 02/Mar/23

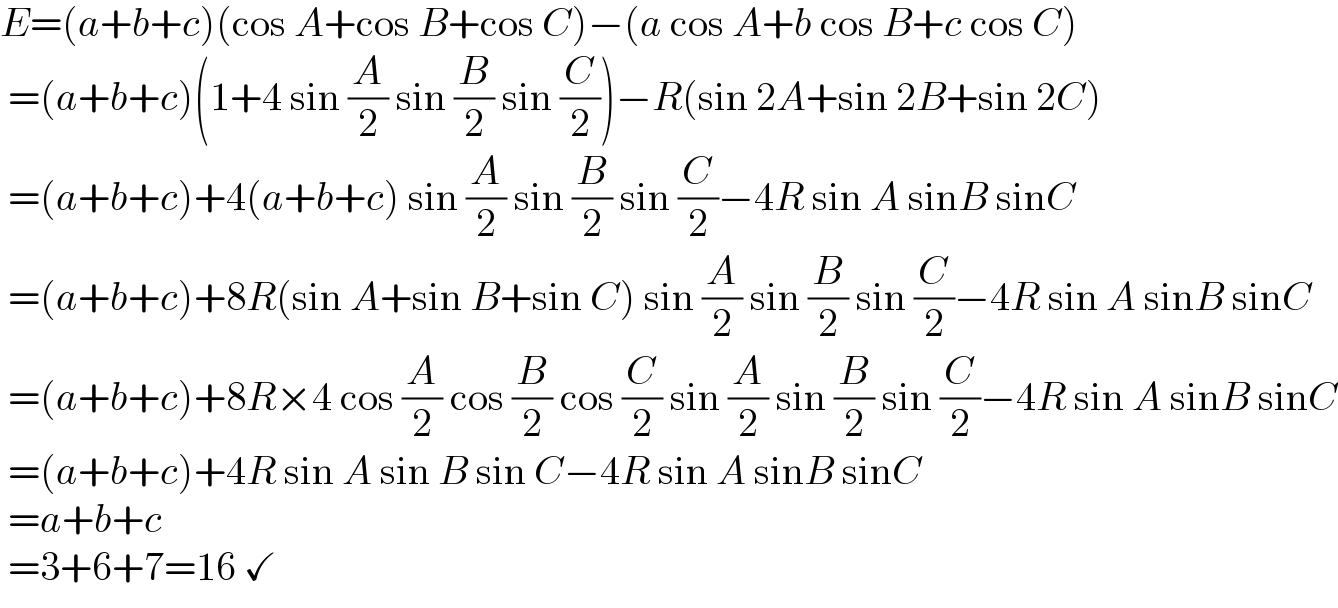
E=(a+b+c)(cos A+cos B+cos C)−(a cos A+b cos B+c cos C) =(a+b+c)(1+4 sin (A/2) sin (B/2) sin (C/2))−R(sin 2A+sin 2B+sin 2C) =(a+b+c)+4(a+b+c) sin (A/2) sin (B/2) sin (C/2)−4R sin A sinB sinC =(a+b+c)+8R(sin A+sin B+sin C) sin (A/2) sin (B/2) sin (C/2)−4R sin A sinB sinC =(a+b+c)+8R×4 cos (A/2) cos (B/2) cos (C/2) sin (A/2) sin (B/2) sin (C/2)−4R sin A sinB sinC =(a+b+c)+4R sin A sin B sin C−4R sin A sinB sinC =a+b+c =3+6+7=16 ✓

$${E}=\left({a}+{b}+{c}\right)\left(\mathrm{cos}\:{A}+\mathrm{cos}\:{B}+\mathrm{cos}\:{C}\right)−\left({a}\:\mathrm{cos}\:{A}+{b}\:\mathrm{cos}\:{B}+{c}\:\mathrm{cos}\:{C}\right) \\ $$$$\:=\left({a}+{b}+{c}\right)\left(\mathrm{1}+\mathrm{4}\:\mathrm{sin}\:\frac{{A}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{B}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{C}}{\mathrm{2}}\right)−{R}\left(\mathrm{sin}\:\mathrm{2}{A}+\mathrm{sin}\:\mathrm{2}{B}+\mathrm{sin}\:\mathrm{2}{C}\right) \\ $$$$\:=\left({a}+{b}+{c}\right)+\mathrm{4}\left({a}+{b}+{c}\right)\:\mathrm{sin}\:\frac{{A}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{B}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{C}}{\mathrm{2}}−\mathrm{4}{R}\:\mathrm{sin}\:{A}\:\mathrm{sin}{B}\:\mathrm{sin}{C} \\ $$$$\:=\left({a}+{b}+{c}\right)+\mathrm{8}{R}\left(\mathrm{sin}\:{A}+\mathrm{sin}\:{B}+\mathrm{sin}\:{C}\right)\:\mathrm{sin}\:\frac{{A}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{B}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{C}}{\mathrm{2}}−\mathrm{4}{R}\:\mathrm{sin}\:{A}\:\mathrm{sin}{B}\:\mathrm{sin}{C} \\ $$$$\:=\left({a}+{b}+{c}\right)+\mathrm{8}{R}×\mathrm{4}\:\mathrm{cos}\:\frac{{A}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{C}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{A}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{B}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{C}}{\mathrm{2}}−\mathrm{4}{R}\:\mathrm{sin}\:{A}\:\mathrm{sin}{B}\:\mathrm{sin}{C} \\ $$$$\:=\left({a}+{b}+{c}\right)+\mathrm{4}{R}\:\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}−\mathrm{4}{R}\:\mathrm{sin}\:{A}\:\mathrm{sin}{B}\:\mathrm{sin}{C} \\ $$$$\:={a}+{b}+{c} \\ $$$$\:=\mathrm{3}+\mathrm{6}+\mathrm{7}=\mathrm{16}\:\checkmark \\ $$

Commented by manxsol last updated on 03/Mar/23

perpendicular projection

$${perpendicular}\:{projection} \\ $$

Commented by manxsol last updated on 03/Mar/23

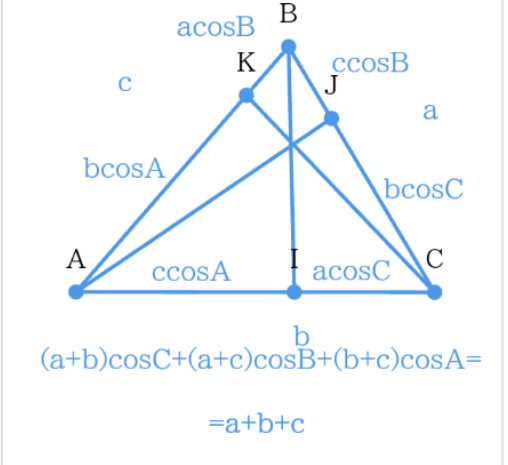
Commented by mnjuly1970 last updated on 03/Mar/23

thanks alot sir W

$${thanks}\:{alot}\:{sir}\:{W} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com