
Previous in Relation and Functions Next in Relation and Functions
Question Number 67518 by mathmax by abdo last updated on 28/Aug/19

$${if}\:{z}\:={x}+{iy}\:\:\:{find}\:\:{lnz}\:\:{interms}\:{of}\:{x}\:{and}\:{y} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 30/Aug/19
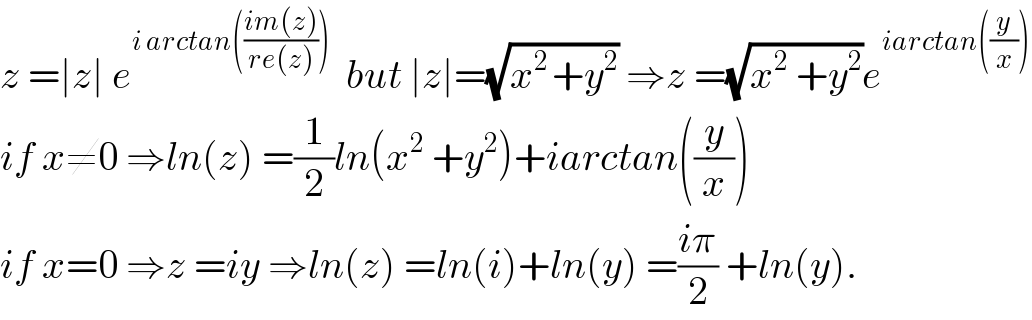
$${z}\:=\mid{z}\mid\:{e}^{{i}\:{arctan}\left(\frac{{im}\left({z}\right)}{{re}\left({z}\right)}\right)} \:\:{but}\:\mid{z}\mid=\sqrt{{x}^{\mathrm{2}\:} +{y}^{\mathrm{2}} }\:\Rightarrow{z}\:=\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }{e}^{{iarctan}\left(\frac{{y}}{{x}}\right)} \\ $$$${if}\:{x}\neq\mathrm{0}\:\Rightarrow{ln}\left({z}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \right)+{iarctan}\left(\frac{{y}}{{x}}\right) \\ $$$${if}\:{x}=\mathrm{0}\:\Rightarrow{z}\:={iy}\:\Rightarrow{ln}\left({z}\right)\:={ln}\left({i}\right)+{ln}\left({y}\right)\:=\frac{{i}\pi}{\mathrm{2}}\:+{ln}\left({y}\right). \\ $$
Answered by mr W last updated on 28/Aug/19
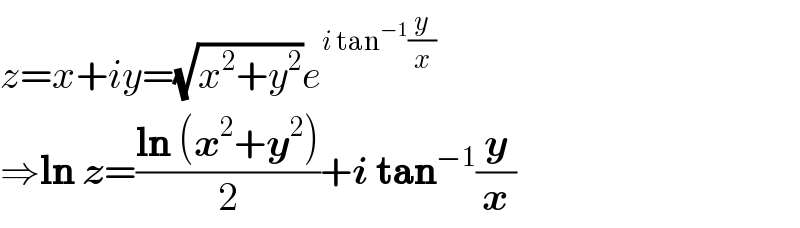
$${z}={x}+{iy}=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{e}^{{i}\:\mathrm{tan}^{−\mathrm{1}} \frac{{y}}{{x}}} \\ $$$$\Rightarrow\boldsymbol{\mathrm{ln}}\:\boldsymbol{{z}}=\frac{\boldsymbol{\mathrm{ln}}\:\left(\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} \right)}{\mathrm{2}}+\boldsymbol{{i}}\:\boldsymbol{\mathrm{tan}}^{−\mathrm{1}} \frac{\boldsymbol{{y}}}{\boldsymbol{{x}}} \\ $$
