Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 145763 by gsk2684 last updated on 07/Jul/21

if z=(((3+i sin θ)/(4−i cos θ)))is purely real and (Π/2)<θ<Π then find arg(sin θ +i cos θ)?

$${if}\:{z}=\left(\frac{\mathrm{3}+{i}\:\mathrm{sin}\:\theta}{\mathrm{4}−{i}\:\mathrm{cos}\:\theta}\right){is}\:{purely}\:{real}\:{and}\: \\ $$$$\frac{\Pi}{\mathrm{2}}<\theta<\Pi\:{then}\:{find}\:{arg}\left(\mathrm{sin}\:\theta\:+{i}\:\mathrm{cos}\:\theta\right)? \\ $$

Answered by mathmax by abdo last updated on 08/Jul/21

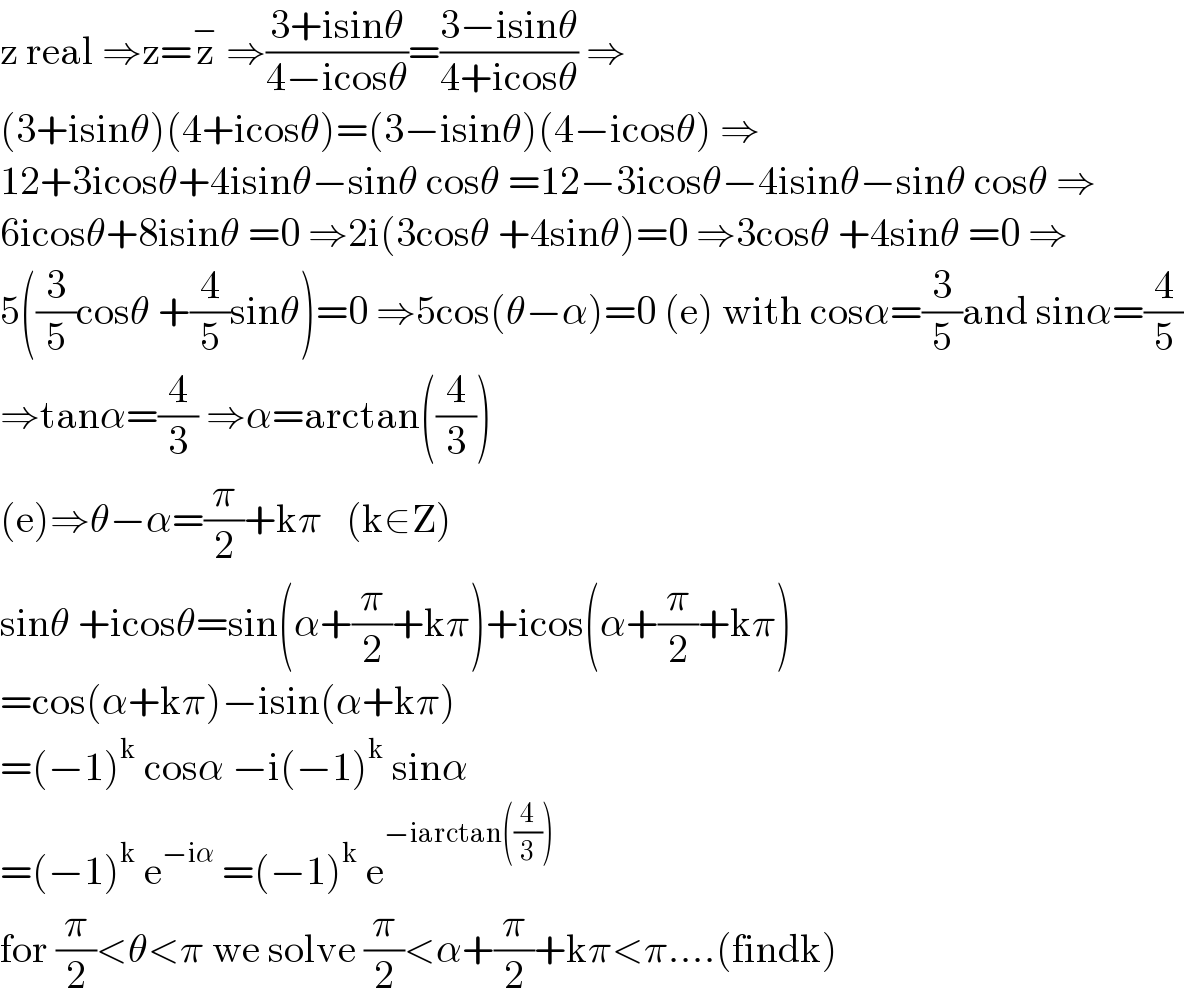
z real ⇒z=z^− ⇒((3+isinθ)/(4−icosθ))=((3−isinθ)/(4+icosθ)) ⇒ (3+isinθ)(4+icosθ)=(3−isinθ)(4−icosθ) ⇒ 12+3icosθ+4isinθ−sinθ cosθ =12−3icosθ−4isinθ−sinθ cosθ ⇒ 6icosθ+8isinθ =0 ⇒2i(3cosθ +4sinθ)=0 ⇒3cosθ +4sinθ =0 ⇒ 5((3/5)cosθ +(4/5)sinθ)=0 ⇒5cos(θ−α)=0 (e) with cosα=(3/5)and sinα=(4/5) ⇒tanα=(4/3) ⇒α=arctan((4/3)) (e)⇒θ−α=(π/2)+kπ (k∈Z) sinθ +icosθ=sin(α+(π/2)+kπ)+icos(α+(π/2)+kπ) =cos(α+kπ)−isin(α+kπ) =(−1)^k cosα −i(−1)^k sinα =(−1)^k e^(−iα) =(−1)^k e^(−iarctan((4/3))) for (π/2)<θ<π we solve (π/2)<α+(π/2)+kπ<π....(findk)

$$\mathrm{z}\:\mathrm{real}\:\Rightarrow\mathrm{z}=\overset{−} {\mathrm{z}}\:\Rightarrow\frac{\mathrm{3}+\mathrm{isin}\theta}{\mathrm{4}−\mathrm{icos}\theta}=\frac{\mathrm{3}−\mathrm{isin}\theta}{\mathrm{4}+\mathrm{icos}\theta}\:\Rightarrow \\ $$$$\left(\mathrm{3}+\mathrm{isin}\theta\right)\left(\mathrm{4}+\mathrm{icos}\theta\right)=\left(\mathrm{3}−\mathrm{isin}\theta\right)\left(\mathrm{4}−\mathrm{icos}\theta\right)\:\Rightarrow \\ $$$$\mathrm{12}+\mathrm{3icos}\theta+\mathrm{4isin}\theta−\mathrm{sin}\theta\:\mathrm{cos}\theta\:=\mathrm{12}−\mathrm{3icos}\theta−\mathrm{4isin}\theta−\mathrm{sin}\theta\:\mathrm{cos}\theta\:\Rightarrow \\ $$$$\mathrm{6icos}\theta+\mathrm{8isin}\theta\:=\mathrm{0}\:\Rightarrow\mathrm{2i}\left(\mathrm{3cos}\theta\:+\mathrm{4sin}\theta\right)=\mathrm{0}\:\Rightarrow\mathrm{3cos}\theta\:+\mathrm{4sin}\theta\:=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{5}\left(\frac{\mathrm{3}}{\mathrm{5}}\mathrm{cos}\theta\:+\frac{\mathrm{4}}{\mathrm{5}}\mathrm{sin}\theta\right)=\mathrm{0}\:\Rightarrow\mathrm{5cos}\left(\theta−\alpha\right)=\mathrm{0}\:\left(\mathrm{e}\right)\:\mathrm{with}\:\mathrm{cos}\alpha=\frac{\mathrm{3}}{\mathrm{5}}\mathrm{and}\:\mathrm{sin}\alpha=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\Rightarrow\mathrm{tan}\alpha=\frac{\mathrm{4}}{\mathrm{3}}\:\Rightarrow\alpha=\mathrm{arctan}\left(\frac{\mathrm{4}}{\mathrm{3}}\right) \\ $$$$\left(\mathrm{e}\right)\Rightarrow\theta−\alpha=\frac{\pi}{\mathrm{2}}+\mathrm{k}\pi\:\:\:\left(\mathrm{k}\in\mathrm{Z}\right) \\ $$$$\mathrm{sin}\theta\:+\mathrm{icos}\theta=\mathrm{sin}\left(\alpha+\frac{\pi}{\mathrm{2}}+\mathrm{k}\pi\right)+\mathrm{icos}\left(\alpha+\frac{\pi}{\mathrm{2}}+\mathrm{k}\pi\right) \\ $$$$=\mathrm{cos}\left(\alpha+\mathrm{k}\pi\right)−\mathrm{isin}\left(\alpha+\mathrm{k}\pi\right) \\ $$$$=\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{cos}\alpha\:−\mathrm{i}\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{sin}\alpha \\ $$$$=\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{e}^{−\mathrm{i}\alpha} \:=\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{e}^{−\mathrm{iarctan}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)} \\ $$$$\mathrm{for}\:\frac{\pi}{\mathrm{2}}<\theta<\pi\:\mathrm{we}\:\mathrm{solve}\:\frac{\pi}{\mathrm{2}}<\alpha+\frac{\pi}{\mathrm{2}}+\mathrm{k}\pi<\pi....\left(\mathrm{findk}\right) \\ $$

Commented by gsk2684 last updated on 08/Jul/21

thank you

$${thank}\:{you}\: \\ $$

Commented by mathmax by abdo last updated on 09/Jul/21

you are welcome

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com