Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 17065 by mrW1 last updated on 30/Jun/17

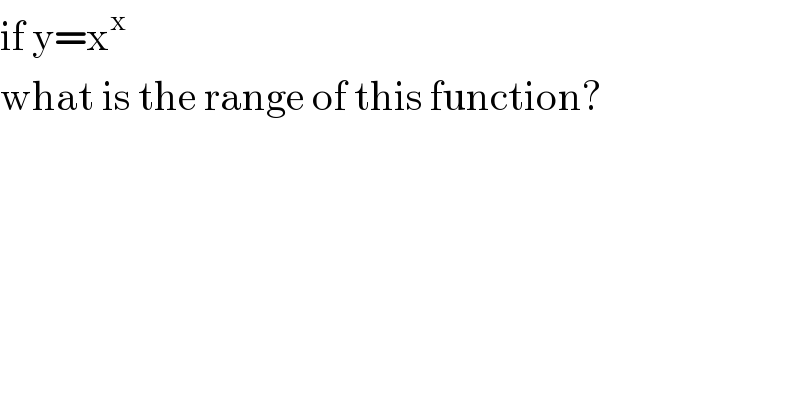
if y=x^x what is the range of this function?

$$\mathrm{if}\:\mathrm{y}=\mathrm{x}^{\mathrm{x}} \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{range}\:\mathrm{of}\:\mathrm{this}\:\mathrm{function}? \\ $$

Commented by ajfour last updated on 30/Jun/17

y∈[e^(−1/e) ,∞).

$$\mathrm{y}\in\left[\mathrm{e}^{−\mathrm{1}/\mathrm{e}} ,\infty\right). \\ $$

Commented by mrW1 last updated on 30/Jun/17

that′s right.

$$\mathrm{that}'\mathrm{s}\:\mathrm{right}. \\ $$

Commented by ajfour last updated on 30/Jun/17

Sir, i evaluated lim_(x→0) x^x taking logarithm , got 1.Then found (dy/dx), saw it is −ve at the start and zero for x=(1/e), and is +ve thereafter. so the minimum of x^x =((1/e))^(1/e) .

$$\mathrm{Sir},\:\mathrm{i}\:\mathrm{evaluated}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{x}^{\boldsymbol{\mathrm{x}}} \:\mathrm{taking} \\ $$$$\mathrm{logarithm}\:,\:\mathrm{got}\:\mathrm{1}.\mathrm{Then}\:\mathrm{found} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}},\:\mathrm{saw}\:\mathrm{it}\:\mathrm{is}\:−\mathrm{ve}\:\mathrm{at}\:\mathrm{the}\:\mathrm{start}\:\mathrm{and} \\ $$$$\mathrm{zero}\:\mathrm{for}\:\mathrm{x}=\frac{\mathrm{1}}{\mathrm{e}},\:\mathrm{and}\:\mathrm{is}\:+\mathrm{ve}\:\mathrm{thereafter}. \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{of}\:\mathrm{x}^{\boldsymbol{\mathrm{x}}} =\left(\frac{\mathrm{1}}{\boldsymbol{\mathrm{e}}}\right)^{\mathrm{1}/\boldsymbol{\mathrm{e}}} . \\ $$

Commented by mrW1 last updated on 30/Jun/17

I would also do like this and find the minimum of the function which is ((1/e))^(1/e) =e^(−(1/e)) =(1/(^e (√e))) But there is also an alternative way. y=x^x the inverse function is x=((ln y)/(W(ln y))) with W=lambert function its domain is −(1/e)≤ln y<∞ or e^(−(1/e)) ≤y<∞

$$\mathrm{I}\:\mathrm{would}\:\mathrm{also}\:\mathrm{do}\:\mathrm{like}\:\mathrm{this}\:\mathrm{and}\:\mathrm{find}\:\mathrm{the} \\ $$$$\mathrm{minimum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{function}\:\mathrm{which}\:\mathrm{is} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{e}}\right)^{\frac{\mathrm{1}}{\mathrm{e}}} =\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{e}}} =\frac{\mathrm{1}}{\:^{\mathrm{e}} \sqrt{\mathrm{e}}} \\ $$$$ \\ $$$$\mathrm{But}\:\mathrm{there}\:\mathrm{is}\:\mathrm{also}\:\mathrm{an}\:\mathrm{alternative}\:\mathrm{way}.\: \\ $$$$\mathrm{y}=\mathrm{x}^{\mathrm{x}} \\ $$$$\mathrm{the}\:\mathrm{inverse}\:\mathrm{function}\:\mathrm{is} \\ $$$$\mathrm{x}=\frac{\mathrm{ln}\:\mathrm{y}}{\mathrm{W}\left(\mathrm{ln}\:\mathrm{y}\right)}\:\mathrm{with}\:\mathrm{W}=\mathrm{lambert}\:\mathrm{function} \\ $$$$\mathrm{its}\:\mathrm{domain}\:\mathrm{is}\:−\frac{\mathrm{1}}{\mathrm{e}}\leqslant\mathrm{ln}\:\mathrm{y}<\infty\:\mathrm{or} \\ $$$$\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{e}}} \leqslant\mathrm{y}<\infty \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com