Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 25567 by rita1608 last updated on 11/Dec/17

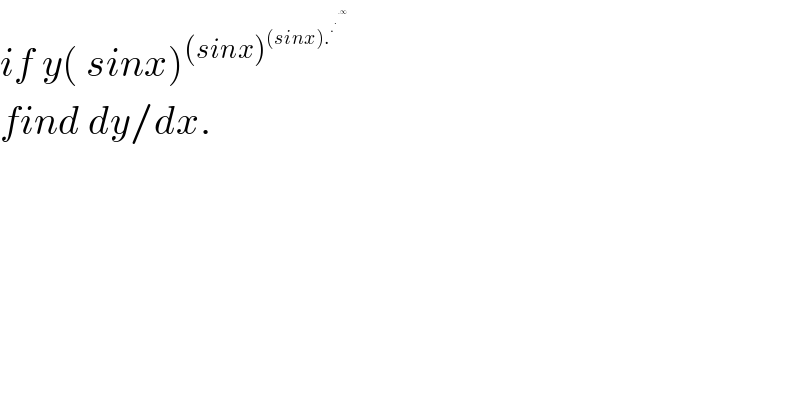
if y( sinx)^((sinx)^((sinx).^.^.^(.∞) ) ) find dy/dx.

$${if}\:{y}\left(\:{sinx}\right)^{\left({sinx}\right)^{\left({sinx}\right).^{.^{.^{.\infty} } } } } \\ $$$${find}\:{dy}/{dx}. \\ $$

Commented by prakash jain last updated on 11/Dec/17

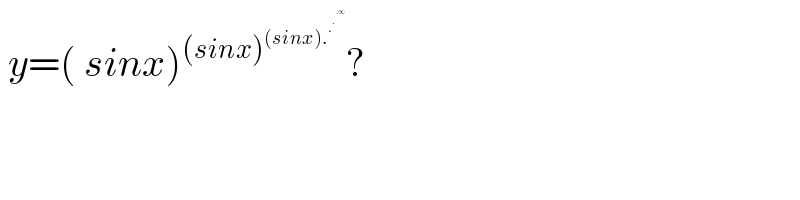
y=( sinx)^((sinx)^((sinx).^.^.^(.∞) ) ) ?

$$\:{y}=\left(\:{sinx}\right)^{\left({sinx}\right)^{\left({sinx}\right).^{.^{.^{.\infty} } } } } ? \\ $$$$ \\ $$

Answered by prakash jain last updated on 11/Dec/17

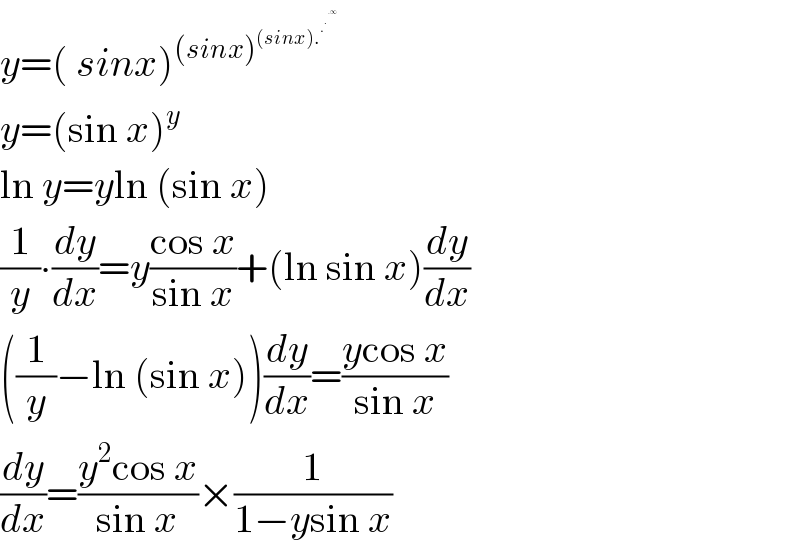
y=( sinx)^((sinx)^((sinx).^.^.^(.∞) ) ) y=(sin x)^y ln y=yln (sin x) (1/y)∙(dy/dx)=y((cos x)/(sin x))+(ln sin x)(dy/dx) ((1/y)−ln (sin x))(dy/dx)=((ycos x)/(sin x)) (dy/dx)=((y^2 cos x)/(sin x))×(1/(1−ysin x))

$${y}=\left(\:{sinx}\right)^{\left({sinx}\right)^{\left({sinx}\right).^{.^{.^{.\infty} } } } } \\ $$$${y}=\left(\mathrm{sin}\:{x}\right)^{{y}} \\ $$$$\mathrm{ln}\:{y}={y}\mathrm{ln}\:\left(\mathrm{sin}\:{x}\right) \\ $$$$\frac{\mathrm{1}}{{y}}\centerdot\frac{{dy}}{{dx}}={y}\frac{\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}}+\left(\mathrm{ln}\:\mathrm{sin}\:{x}\right)\frac{{dy}}{{dx}} \\ $$$$\left(\frac{\mathrm{1}}{{y}}−\mathrm{ln}\:\left(\mathrm{sin}\:{x}\right)\right)\frac{{dy}}{{dx}}=\frac{{y}\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}} \\ $$$$\frac{{dy}}{{dx}}=\frac{{y}^{\mathrm{2}} \mathrm{cos}\:{x}}{\mathrm{sin}\:{x}}×\frac{\mathrm{1}}{\mathrm{1}−{y}\mathrm{sin}\:{x}} \\ $$

Commented by rita1608 last updated on 11/Dec/17

thank u sir

$${thank}\:{u}\:{sir} \\ $$

Commented by mrW1 last updated on 11/Dec/17

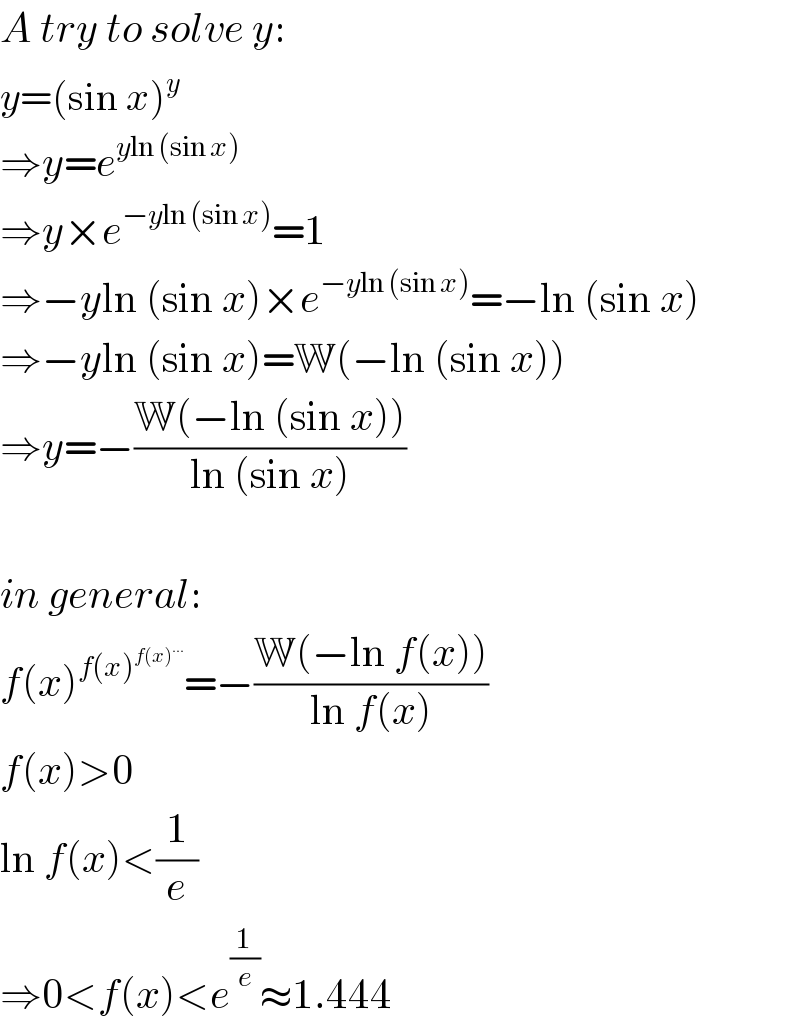
A try to solve y: y=(sin x)^y ⇒y=e^(yln (sin x)) ⇒y×e^(−yln (sin x)) =1 ⇒−yln (sin x)×e^(−yln (sin x)) =−ln (sin x) ⇒−yln (sin x)=W(−ln (sin x)) ⇒y=−((W(−ln (sin x)))/(ln (sin x))) in general: f(x)^(f(x)^(f(x)^(...) ) ) =−((W(−ln f(x)))/(ln f(x))) f(x)>0 ln f(x)<(1/e) ⇒0<f(x)<e^(1/e) ≈1.444

$${A}\:{try}\:{to}\:{solve}\:{y}: \\ $$$${y}=\left(\mathrm{sin}\:{x}\right)^{{y}} \\ $$$$\Rightarrow{y}={e}^{{y}\mathrm{ln}\:\left(\mathrm{sin}\:{x}\right)} \\ $$$$\Rightarrow{y}×{e}^{−{y}\mathrm{ln}\:\left(\mathrm{sin}\:{x}\right)} =\mathrm{1} \\ $$$$\Rightarrow−{y}\mathrm{ln}\:\left(\mathrm{sin}\:{x}\right)×{e}^{−{y}\mathrm{ln}\:\left(\mathrm{sin}\:{x}\right)} =−\mathrm{ln}\:\left(\mathrm{sin}\:{x}\right) \\ $$$$\Rightarrow−{y}\mathrm{ln}\:\left(\mathrm{sin}\:{x}\right)=\mathbb{W}\left(−\mathrm{ln}\:\left(\mathrm{sin}\:{x}\right)\right) \\ $$$$\Rightarrow{y}=−\frac{\mathbb{W}\left(−\mathrm{ln}\:\left(\mathrm{sin}\:{x}\right)\right)}{\mathrm{ln}\:\left(\mathrm{sin}\:{x}\right)} \\ $$$$ \\ $$$${in}\:{general}: \\ $$$${f}\left({x}\right)^{{f}\left({x}\right)^{{f}\left({x}\right)^{...} } } =−\frac{\mathbb{W}\left(−\mathrm{ln}\:{f}\left({x}\right)\right)}{\mathrm{ln}\:{f}\left({x}\right)} \\ $$$${f}\left({x}\right)>\mathrm{0} \\ $$$$\mathrm{ln}\:{f}\left({x}\right)<\frac{\mathrm{1}}{{e}} \\ $$$$\Rightarrow\mathrm{0}<{f}\left({x}\right)<{e}^{\frac{\mathrm{1}}{{e}}} \approx\mathrm{1}.\mathrm{444} \\ $$

Answered by ibraheem160 last updated on 11/Dec/17

Terms of Service

Privacy Policy

Contact: info@tinkutara.com