
Question Number 101558 by mhmd last updated on 03/Jul/20

$${if}\:{y}={sin}\mathrm{2}{x}\:{is}\:{the}\:{solution}\:{of}\:{differintial}\:{equation}\: \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:+\mathrm{4}{y}={k}\:{then}\:{the}\:{k}\:{is}\:....... \\ $$
Answered by bemath last updated on 03/Jul/20
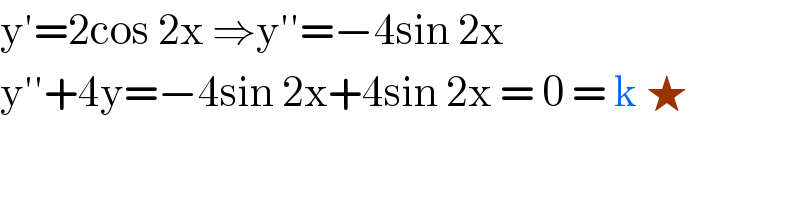
$$\mathrm{y}'=\mathrm{2cos}\:\mathrm{2x}\:\Rightarrow\mathrm{y}''=−\mathrm{4sin}\:\mathrm{2x} \\ $$$$\mathrm{y}''+\mathrm{4y}=−\mathrm{4sin}\:\mathrm{2x}+\mathrm{4sin}\:\mathrm{2x}\:=\:\mathrm{0}\:=\:\mathrm{k}\:\bigstar \\ $$
Commented by mhmd last updated on 03/Jul/20

$${thank}\:{you}\:{sir} \\ $$
