
Question Number 43489 by peter frank last updated on 11/Sep/18
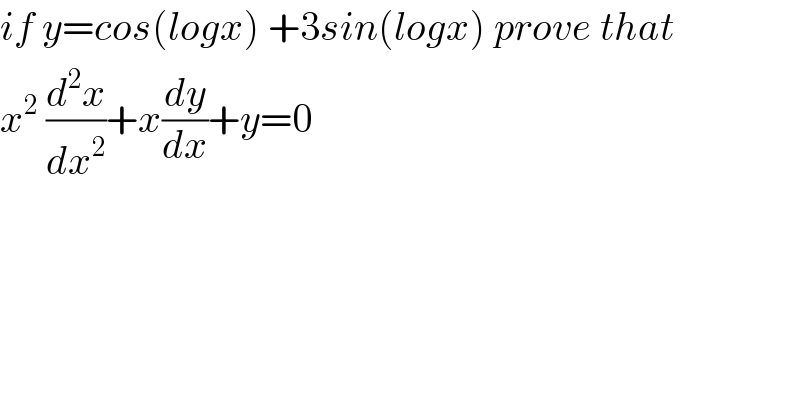
$${if}\:{y}={cos}\left({logx}\right)\:+\mathrm{3}{sin}\left({logx}\right)\:{prove}\:{that} \\ $$$${x}^{\mathrm{2}} \:\frac{{d}^{\mathrm{2}} {x}}{{dx}^{\mathrm{2}} }+{x}\frac{{dy}}{{dx}}+{y}=\mathrm{0} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 11/Sep/18
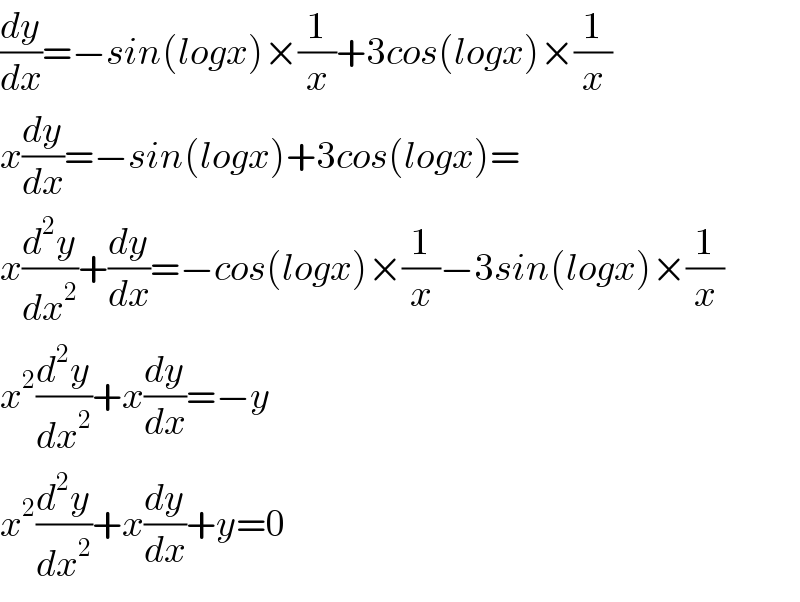
$$\frac{{dy}}{{dx}}=−{sin}\left({logx}\right)×\frac{\mathrm{1}}{{x}}+\mathrm{3}{cos}\left({logx}\right)×\frac{\mathrm{1}}{{x}} \\ $$$${x}\frac{{dy}}{{dx}}=−{sin}\left({logx}\right)+\mathrm{3}{cos}\left({logx}\right)= \\ $$$${x}\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\frac{{dy}}{{dx}}=−{cos}\left({logx}\right)×\frac{\mathrm{1}}{{x}}−\mathrm{3}{sin}\left({logx}\right)×\frac{\mathrm{1}}{{x}} \\ $$$${x}^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+{x}\frac{{dy}}{{dx}}=−{y} \\ $$$${x}^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+{x}\frac{{dy}}{{dx}}+{y}=\mathrm{0} \\ $$
Commented by peter frank last updated on 11/Sep/18

$${much}\:{respect}\:{sir} \\ $$
