Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 196629 by universe last updated on 28/Aug/23

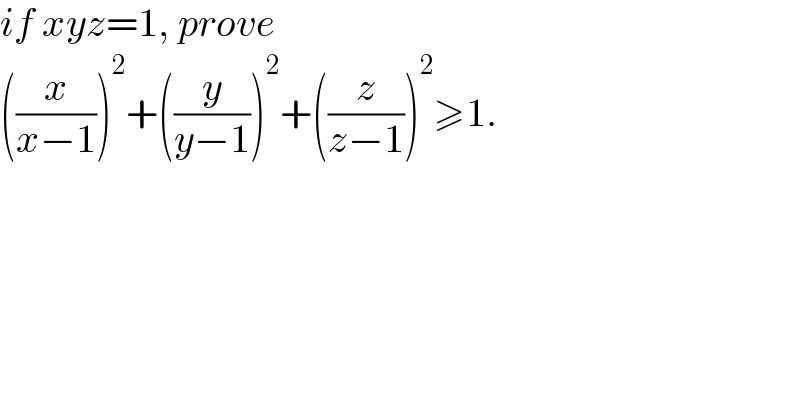
if xyz=1, prove ((x/(x−1)))^2 +((y/(y−1)))^2 +((z/(z−1)))^2 ≥1.

$${if}\:{xyz}=\mathrm{1},\:{prove} \\ $$$$\left(\frac{{x}}{{x}−\mathrm{1}}\right)^{\mathrm{2}} +\left(\frac{{y}}{{y}−\mathrm{1}}\right)^{\mathrm{2}} +\left(\frac{{z}}{{z}−\mathrm{1}}\right)^{\mathrm{2}} \geqslant\mathrm{1}. \\ $$

Commented by universe last updated on 28/Aug/23

solution to question #196519

$$ \\ $$$${solution}\:{to}\:{question}\:#\mathrm{196519} \\ $$

Answered by universe last updated on 28/Aug/23

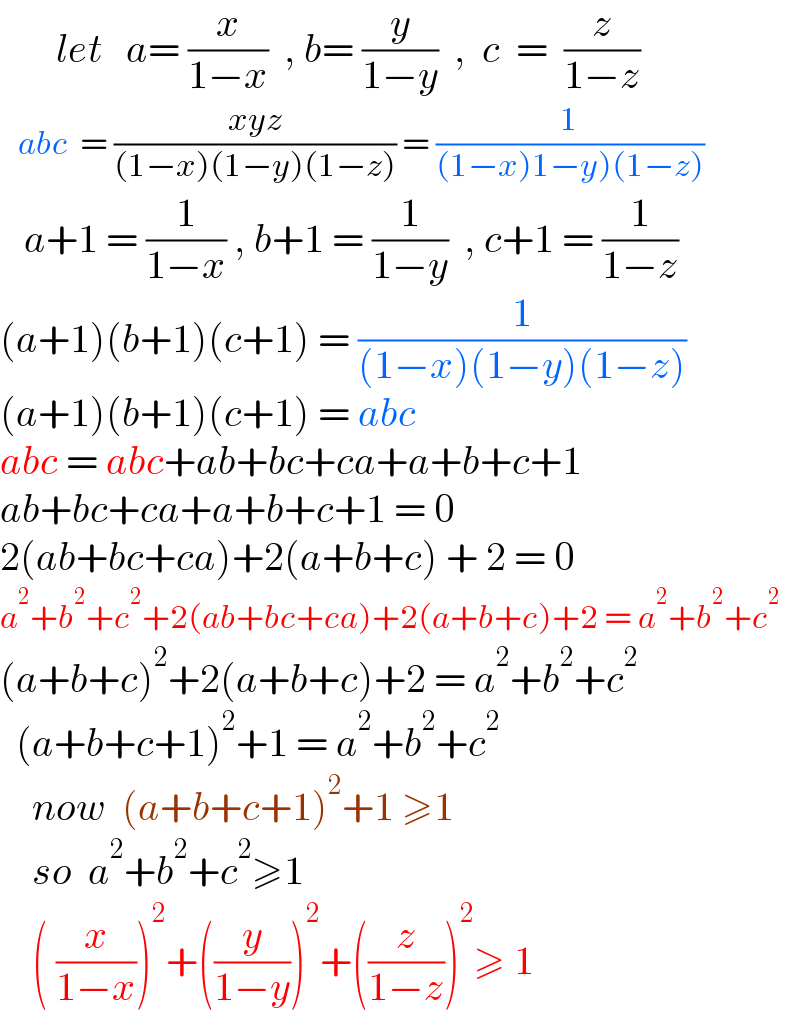
let a= (x/(1−x)) , b= (y/(1−y)) , c = (z/(1−z)) abc = ((xyz)/((1−x)(1−y)(1−z))) = (1/((1−x)1−y)(1−z))) a+1 = (1/(1−x)) , b+1 = (1/(1−y)) , c+1 = (1/(1−z)) (a+1)(b+1)(c+1) = (1/((1−x)(1−y)(1−z))) (a+1)(b+1)(c+1) = abc abc = abc+ab+bc+ca+a+b+c+1 ab+bc+ca+a+b+c+1 = 0 2(ab+bc+ca)+2(a+b+c) + 2 = 0 a^2 +b^2 +c^2 +2(ab+bc+ca)+2(a+b+c)+2 = a^2 +b^2 +c^2 (a+b+c)^2 +2(a+b+c)+2 = a^2 +b^2 +c^2 (a+b+c+1)^2 +1 = a^2 +b^2 +c^2 now (a+b+c+1)^2 +1 ≥1 so a^2 +b^2 +c^2 ≥1 ( (x/(1−x)))^2 +((y/(1−y)))^2 +((z/(1−z)))^2 ≥ 1

$$\:\:\:\:\:\:\:{let}\:\:\:{a}=\:\frac{{x}}{\mathrm{1}−{x}}\:\:,\:{b}=\:\frac{{y}}{\mathrm{1}−{y}}\:\:,\:\:{c}\:\:=\:\:\frac{{z}}{\mathrm{1}−{z}} \\ $$$$\:\:\:{abc}\:\:=\:\frac{{xyz}}{\left(\mathrm{1}−{x}\right)\left(\mathrm{1}−{y}\right)\left(\mathrm{1}−{z}\right)}\:=\:\frac{\mathrm{1}}{\left.\left(\mathrm{1}−{x}\right)\mathrm{1}−{y}\right)\left(\mathrm{1}−{z}\right)} \\ $$$$\:\:\:{a}+\mathrm{1}\:=\:\frac{\mathrm{1}}{\mathrm{1}−{x}}\:,\:{b}+\mathrm{1}\:=\:\frac{\mathrm{1}}{\mathrm{1}−{y}}\:\:,\:{c}+\mathrm{1}\:=\:\frac{\mathrm{1}}{\mathrm{1}−{z}} \\ $$$$\left({a}+\mathrm{1}\right)\left({b}+\mathrm{1}\right)\left({c}+\mathrm{1}\right)\:=\:\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)\left(\mathrm{1}−{y}\right)\left(\mathrm{1}−{z}\right)} \\ $$$$\left({a}+\mathrm{1}\right)\left({b}+\mathrm{1}\right)\left({c}+\mathrm{1}\right)\:=\:{abc} \\ $$$${abc}\:=\:{abc}+{ab}+{bc}+{ca}+{a}+{b}+{c}+\mathrm{1} \\ $$$${ab}+{bc}+{ca}+{a}+{b}+{c}+\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{2}\left({ab}+{bc}+{ca}\right)+\mathrm{2}\left({a}+{b}+{c}\right)\:+\:\mathrm{2}\:=\:\mathrm{0} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}\left({ab}+{bc}+{ca}\right)+\mathrm{2}\left({a}+{b}+{c}\right)+\mathrm{2}\:=\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{2}} +\mathrm{2}\left({a}+{b}+{c}\right)+\mathrm{2}\:=\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \\ $$$$\:\:\left({a}+{b}+{c}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\:=\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \\ $$$$\:\:\:\:{now}\:\:\left({a}+{b}+{c}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\:\geqslant\mathrm{1} \\ $$$$\:\:\:\:{so}\:\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \geqslant\mathrm{1} \\ $$$$\:\:\:\:\left(\:\frac{{x}}{\mathrm{1}−{x}}\right)^{\mathrm{2}} +\left(\frac{{y}}{\mathrm{1}−{y}}\right)^{\mathrm{2}} +\left(\frac{{z}}{\mathrm{1}−{z}}\right)^{\mathrm{2}} \geqslant\:\mathrm{1}\: \\ $$

Commented by mr W last updated on 28/Aug/23

great! thanks!

$${great}!\:{thanks}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com