
Question Number 147582 by mathdanisur last updated on 22/Jul/21
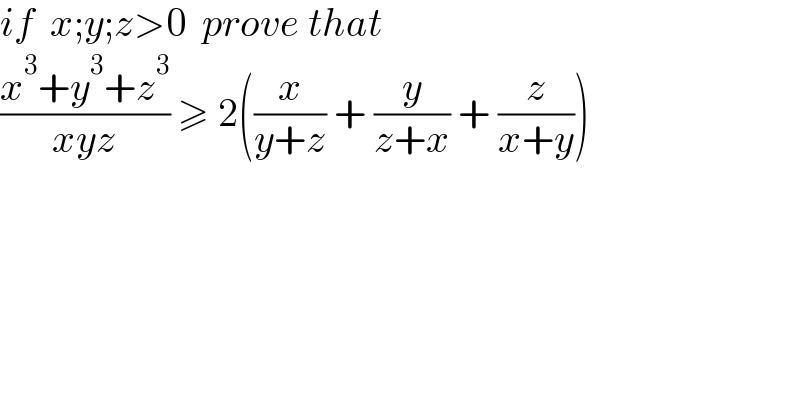
$${if}\:\:{x};{y};{z}>\mathrm{0}\:\:{prove}\:{that} \\ $$$$\frac{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} }{{xyz}}\:\geqslant\:\mathrm{2}\left(\frac{{x}}{{y}+{z}}\:+\:\frac{{y}}{{z}+{x}}\:+\:\frac{{z}}{{x}+{y}}\right) \\ $$
Answered by mitica last updated on 22/Jul/21
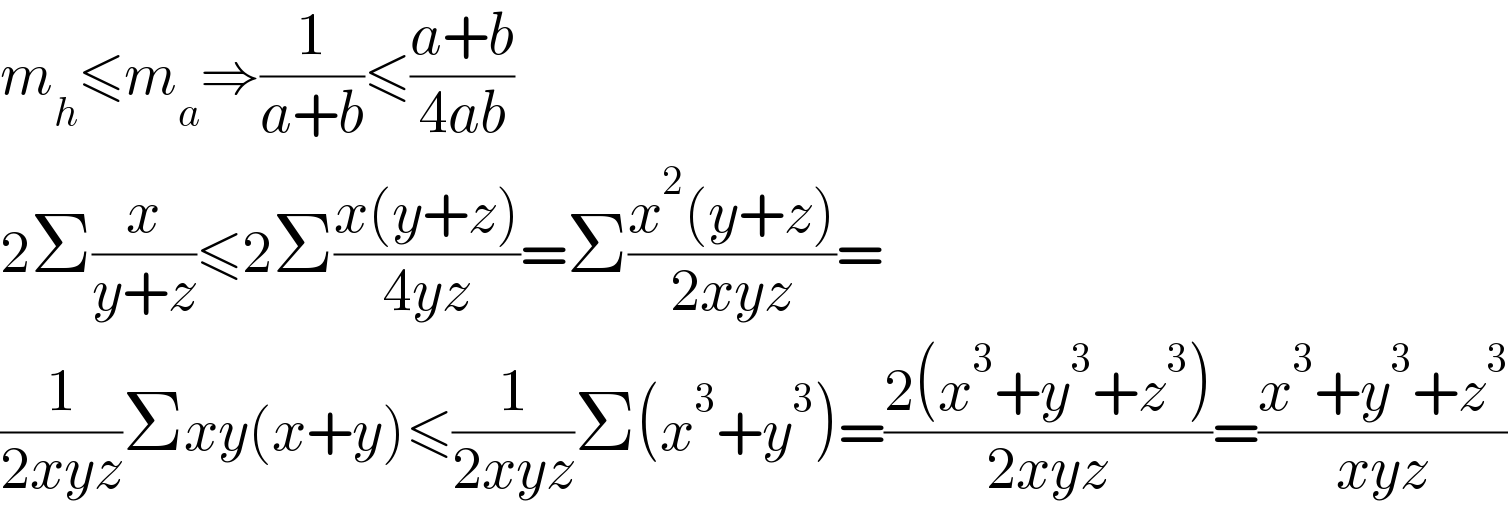
$${m}_{{h}} \leqslant{m}_{{a}} \Rightarrow\frac{\mathrm{1}}{{a}+{b}}\leqslant\frac{{a}+{b}}{\mathrm{4}{ab}} \\ $$$$\mathrm{2}\Sigma\frac{{x}}{{y}+{z}}\leqslant\mathrm{2}\Sigma\frac{{x}\left({y}+{z}\right)}{\mathrm{4}{yz}}=\Sigma\frac{{x}^{\mathrm{2}} \left({y}+{z}\right)}{\mathrm{2}{xyz}}= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{xyz}}\Sigma{xy}\left({x}+{y}\right)\leqslant\frac{\mathrm{1}}{\mathrm{2}{xyz}}\Sigma\left({x}^{\mathrm{3}} +{y}^{\mathrm{3}} \right)=\frac{\mathrm{2}\left({x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} \right)}{\mathrm{2}{xyz}}=\frac{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} }{{xyz}} \\ $$
Commented by mathdanisur last updated on 22/Jul/21

$${Thank}\:{you}\:{Sir} \\ $$
