
Question Number 52713 by F_Nongue last updated on 12/Jan/19
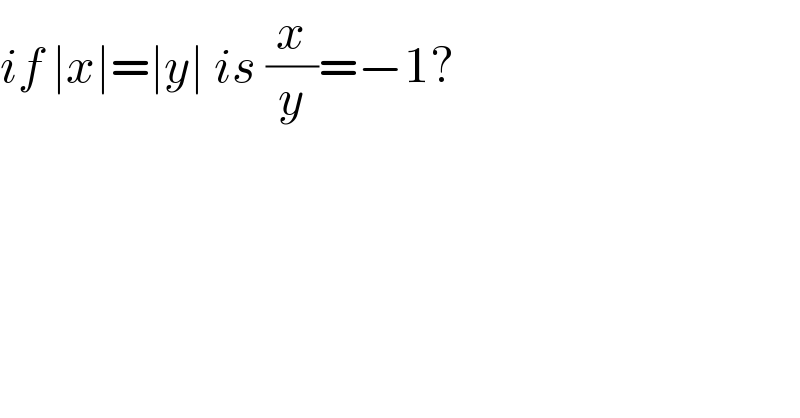
$${if}\:\mid{x}\mid=\mid{y}\mid\:{is}\:\frac{{x}}{{y}}=−\mathrm{1}? \\ $$
Commented by maxmathsup by imad last updated on 12/Jan/19
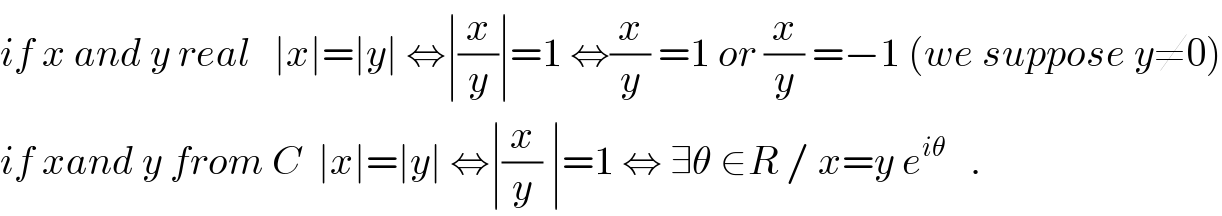
$${if}\:{x}\:{and}\:{y}\:{real}\:\:\:\mid{x}\mid=\mid{y}\mid\:\Leftrightarrow\mid\frac{{x}}{{y}}\mid=\mathrm{1}\:\Leftrightarrow\frac{{x}}{{y}}\:=\mathrm{1}\:{or}\:\frac{{x}}{{y}}\:=−\mathrm{1}\:\left({we}\:{suppose}\:{y}\neq\mathrm{0}\right) \\ $$$${if}\:{xand}\:{y}\:{from}\:{C}\:\:\mid{x}\mid=\mid{y}\mid\:\Leftrightarrow\mid\frac{{x}}{{y}}\:\mid=\mathrm{1}\:\Leftrightarrow\:\exists\theta\:\in{R}\:/\:{x}={y}\:{e}^{{i}\theta} \:\:\:. \\ $$
Answered by Kunal12588 last updated on 12/Jan/19

$$\mid{x}\mid=\mid{y}\mid \\ $$$$\Rightarrow{x}=\pm{y} \\ $$$$\Rightarrow\frac{{x}}{{y}}=\mathrm{1}\:{or}\:\frac{{x}}{{y}}=−\mathrm{1} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 12/Jan/19
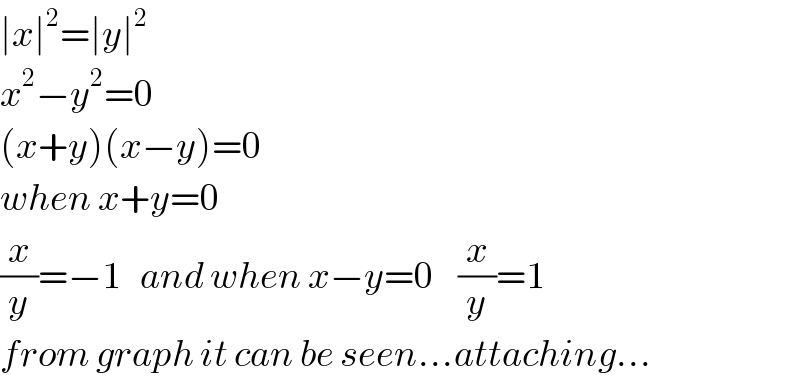
$$\mid{x}\mid^{\mathrm{2}} =\mid{y}\mid^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({x}+{y}\right)\left({x}−{y}\right)=\mathrm{0} \\ $$$${when}\:{x}+{y}=\mathrm{0} \\ $$$$\frac{{x}}{{y}}=−\mathrm{1}\:\:\:{and}\:{when}\:{x}−{y}=\mathrm{0}\:\:\:\:\frac{{x}}{{y}}=\mathrm{1} \\ $$$${from}\:{graph}\:{it}\:{can}\:{be}\:{seen}...{attaching}... \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 12/Jan/19
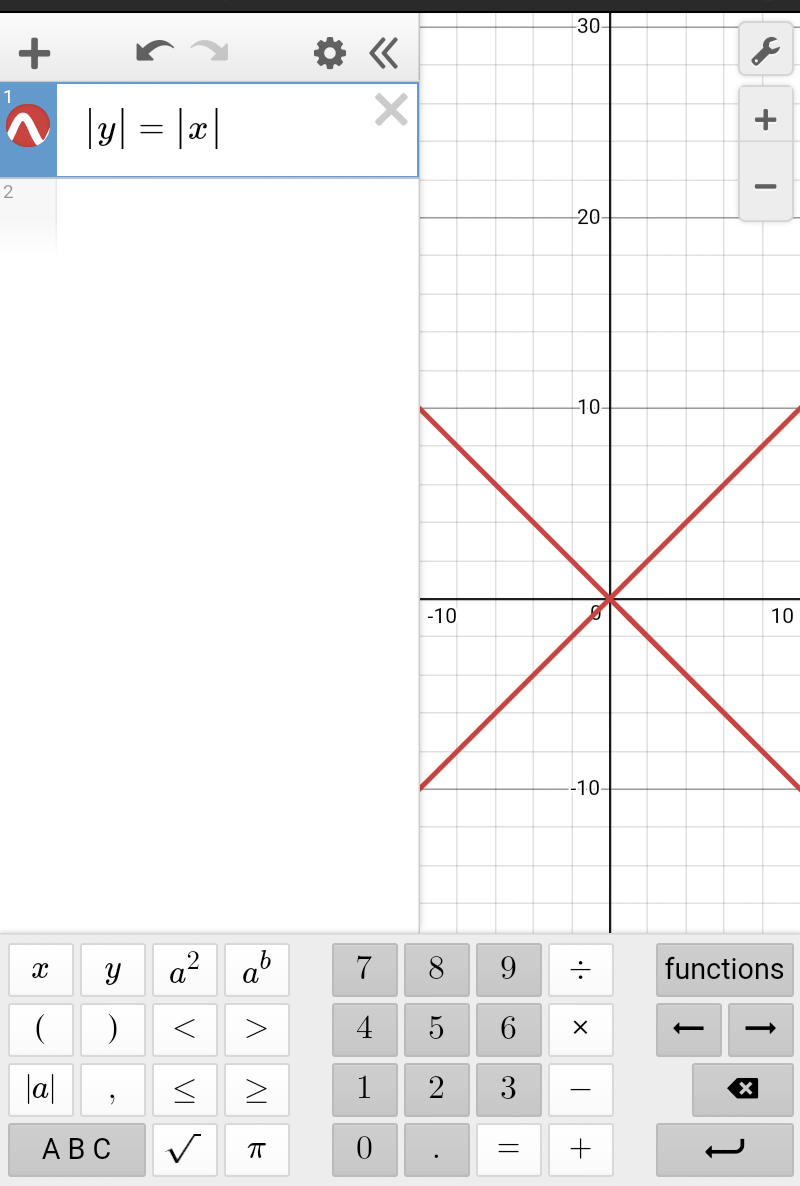
Commented by F_Nongue last updated on 25/Jan/19

$${thanks}\:{sir} \\ $$
