
Question Number 35481 by JOHNMASANJA last updated on 19/May/18
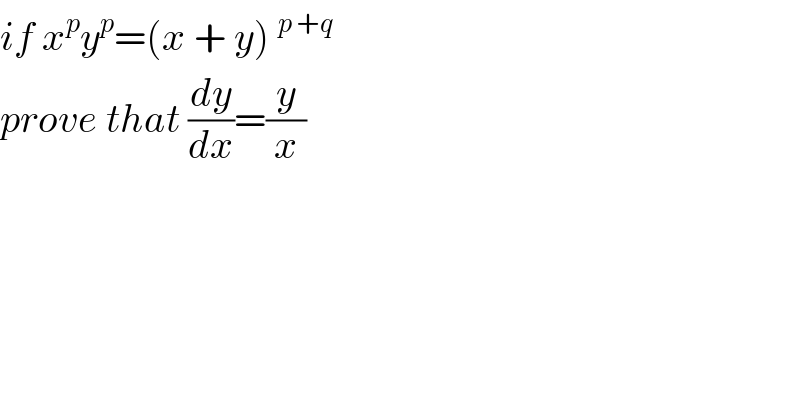
$${if}\:{x}^{{p}} {y}^{{p}} =\left({x}\:+\:{y}\right)\:^{{p}\:+{q}} \:\:\: \\ $$$${prove}\:{that}\:\frac{{dy}}{{dx}}=\frac{{y}}{{x}} \\ $$
Commented by math1967 last updated on 19/May/18
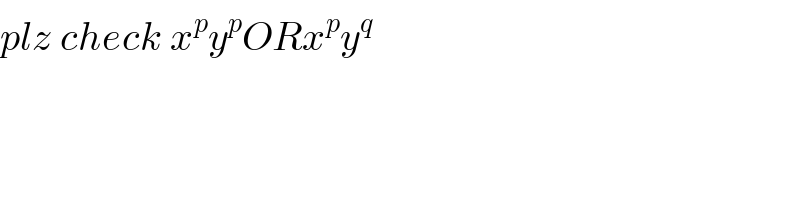
$${plz}\:{check}\:{x}^{{p}} {y}^{{p}} {ORx}^{{p}} {y}^{{q}} \\ $$
Answered by math1967 last updated on 19/May/18
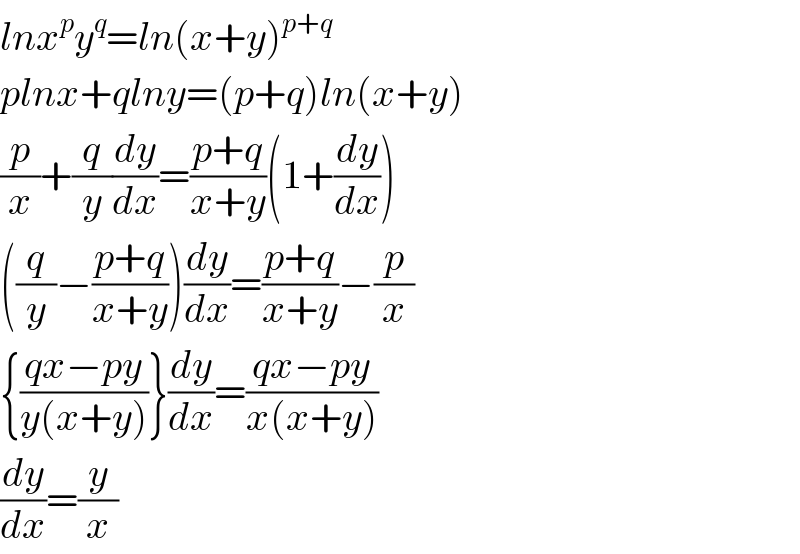
$${lnx}^{{p}} {y}^{{q}} ={ln}\left({x}+{y}\right)^{{p}+{q}} \\ $$$${plnx}+{qlny}=\left({p}+{q}\right){ln}\left({x}+{y}\right) \\ $$$$\frac{{p}}{{x}}+\frac{{q}}{{y}}\frac{{dy}}{{dx}}=\frac{{p}+{q}}{{x}+{y}}\left(\mathrm{1}+\frac{{dy}}{{dx}}\right) \\ $$$$\left(\frac{{q}}{{y}}−\frac{{p}+{q}}{{x}+{y}}\right)\frac{{dy}}{{dx}}=\frac{{p}+{q}}{{x}+{y}}−\frac{{p}}{{x}} \\ $$$$\left\{\frac{{qx}−{py}}{{y}\left({x}+{y}\right)}\right\}\frac{{dy}}{{dx}}=\frac{{qx}−{py}}{{x}\left({x}+{y}\right)} \\ $$$$\frac{{dy}}{{dx}}=\frac{{y}}{{x}} \\ $$
