Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 177579 by mr W last updated on 07/Oct/22

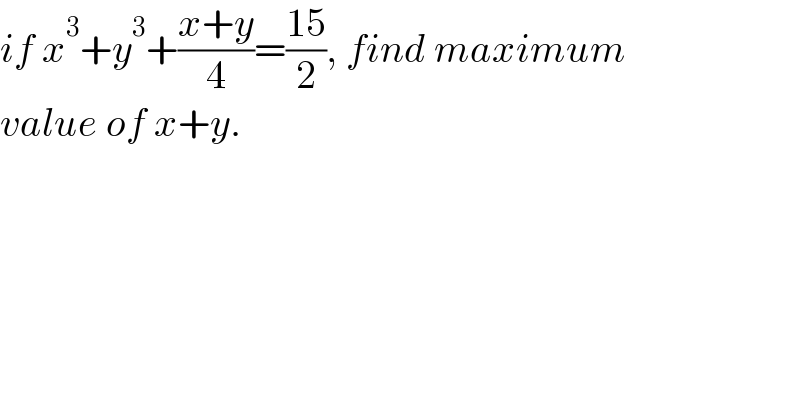
if x^3 +y^3 +((x+y)/4)=((15)/2), find maximum value of x+y.

$${if}\:{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +\frac{{x}+{y}}{\mathrm{4}}=\frac{\mathrm{15}}{\mathrm{2}},\:{find}\:{maximum} \\ $$$${value}\:{of}\:{x}+{y}. \\ $$

Answered by TheHoneyCat last updated on 07/Oct/22

if x=y+ε 15/2=x^3 +y^3 +((x+y)/4) =(y+ε)^3 +y^3 +((2y+ε)/4) =y^3 +3y^2 ε+3yε^2 +ε^3 +y^3 +((2y+ε)/4) =y^3 +y^3 +((y+y)/4) + ε(3y^2 +1/4) +ε^2 (3y) The function in y beeing monotonous This shows that ε needs to be decreese (when y is increesed) if you are to maintain the equation. Basicaly “x+y” is always greater when ε=0. So the problem boils down to finding the max value of 2x when 2x^3 +(x/2)=((15)/2) ⇔4x^3 +x=15 ⇔(x−3/2)(4x^2 +6x+10)=0 Since 6^2 −4×10<0 The only possible solution is thus: x=3/2 (one can verify that it is not a minimum by comparing to values for x=0 and y≠0...)

$$\mathrm{if}\:{x}={y}+\epsilon \\ $$$$\mathrm{15}/\mathrm{2}={x}^{\mathrm{3}} +{y}^{\mathrm{3}} +\frac{{x}+{y}}{\mathrm{4}} \\ $$$$=\left({y}+\epsilon\right)^{\mathrm{3}} +{y}^{\mathrm{3}} +\frac{\mathrm{2}{y}+\epsilon}{\mathrm{4}} \\ $$$$={y}^{\mathrm{3}} +\mathrm{3}{y}^{\mathrm{2}} \epsilon+\mathrm{3}{y}\epsilon^{\mathrm{2}} +\epsilon^{\mathrm{3}} +{y}^{\mathrm{3}} +\frac{\mathrm{2}{y}+\epsilon}{\mathrm{4}} \\ $$$$={y}^{\mathrm{3}} +{y}^{\mathrm{3}} +\frac{{y}+{y}}{\mathrm{4}}\:+\:\epsilon\left(\mathrm{3}{y}^{\mathrm{2}} +\mathrm{1}/\mathrm{4}\right)\:+\epsilon^{\mathrm{2}} \left(\mathrm{3}{y}\right) \\ $$$$ \\ $$$${The}\:{function}\:{in}\:{y}\:{beeing}\:{monotonous} \\ $$$$\mathrm{This}\:\mathrm{shows}\:\mathrm{that}\:\epsilon\:\mathrm{needs}\:\mathrm{to}\:\mathrm{be}\:\mathrm{decreese}\:\left(\mathrm{when}\right. \\ $$$$\left.{y}\:\mathrm{is}\:\mathrm{increesed}\right) \\ $$$$\mathrm{if}\:\mathrm{you}\:\mathrm{are}\:\mathrm{to}\:\mathrm{maintain}\:\mathrm{the}\:\mathrm{equation}. \\ $$$$ \\ $$$$\mathrm{Basicaly}\:``{x}+{y}''\:\mathrm{is}\:\mathrm{always}\:\mathrm{greater}\:\mathrm{when}\:\epsilon=\mathrm{0}. \\ $$$$ \\ $$$$\mathrm{So}\:\mathrm{the}\:\mathrm{problem}\:\mathrm{boils}\:\mathrm{down}\:\mathrm{to}\:\mathrm{finding}\:\mathrm{the}\: \\ $$$$\mathrm{max}\:\mathrm{value}\:\mathrm{of}\:\mathrm{2}{x}\: \\ $$$$\mathrm{when} \\ $$$$\mathrm{2}{x}^{\mathrm{3}} +\frac{{x}}{\mathrm{2}}=\frac{\mathrm{15}}{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{4}{x}^{\mathrm{3}} +{x}=\mathrm{15} \\ $$$$\Leftrightarrow\left({x}−\mathrm{3}/\mathrm{2}\right)\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{10}\right)=\mathrm{0} \\ $$$$\mathrm{Since}\:\mathrm{6}^{\mathrm{2}} −\mathrm{4}×\mathrm{10}<\mathrm{0} \\ $$$$\mathrm{The}\:\mathrm{only}\:\mathrm{possible}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{thus}:\: \\ $$$${x}=\mathrm{3}/\mathrm{2} \\ $$$$ \\ $$$$\left(\mathrm{one}\:\mathrm{can}\:\mathrm{verify}\:\mathrm{that}\:\mathrm{it}\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:\mathrm{minimum}\right. \\ $$$$\left.\mathrm{by}\:\mathrm{comparing}\:\mathrm{to}\:\mathrm{values}\:\mathrm{for}\:{x}=\mathrm{0}\:\mathrm{and}\:\mathrm{y}\neq\mathrm{0}...\right) \\ $$

Commented by mr W last updated on 07/Oct/22

thanks sir!

$${thanks}\:{sir}! \\ $$

Answered by mr W last updated on 07/Oct/22

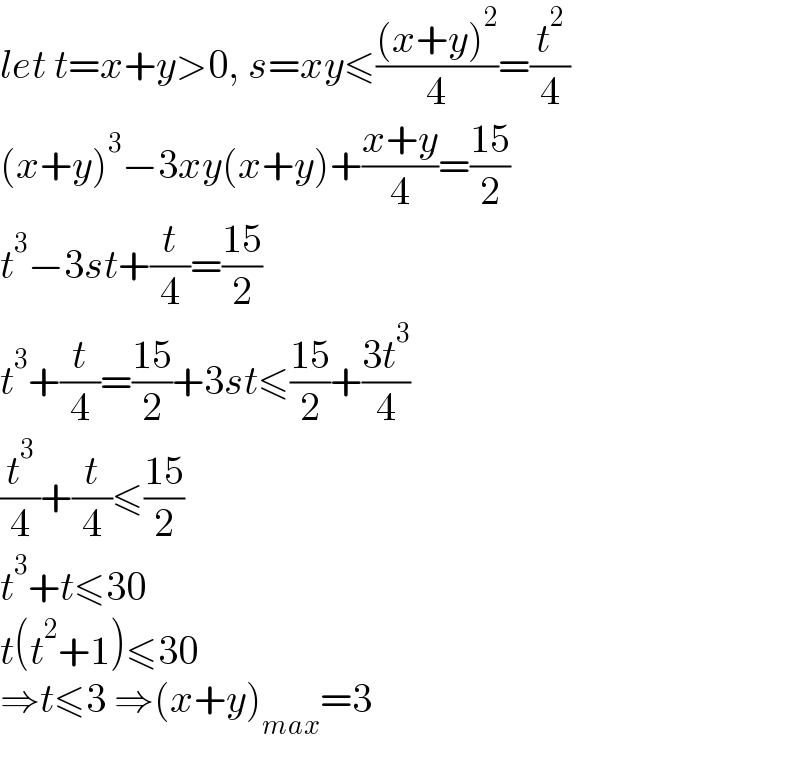
let t=x+y>0, s=xy≤(((x+y)^2 )/4)=(t^2 /4) (x+y)^3 −3xy(x+y)+((x+y)/4)=((15)/2) t^3 −3st+(t/4)=((15)/2) t^3 +(t/4)=((15)/2)+3st≤((15)/2)+((3t^3 )/4) (t^3 /4)+(t/4)≤((15)/2) t^3 +t≤30 t(t^2 +1)≤30 ⇒t≤3 ⇒(x+y)_(max) =3

$${let}\:{t}={x}+{y}>\mathrm{0},\:{s}={xy}\leqslant\frac{\left({x}+{y}\right)^{\mathrm{2}} }{\mathrm{4}}=\frac{{t}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\left({x}+{y}\right)^{\mathrm{3}} −\mathrm{3}{xy}\left({x}+{y}\right)+\frac{{x}+{y}}{\mathrm{4}}=\frac{\mathrm{15}}{\mathrm{2}} \\ $$$${t}^{\mathrm{3}} −\mathrm{3}{st}+\frac{{t}}{\mathrm{4}}=\frac{\mathrm{15}}{\mathrm{2}} \\ $$$${t}^{\mathrm{3}} +\frac{{t}}{\mathrm{4}}=\frac{\mathrm{15}}{\mathrm{2}}+\mathrm{3}{st}\leqslant\frac{\mathrm{15}}{\mathrm{2}}+\frac{\mathrm{3}{t}^{\mathrm{3}} }{\mathrm{4}} \\ $$$$\frac{{t}^{\mathrm{3}} }{\mathrm{4}}+\frac{{t}}{\mathrm{4}}\leqslant\frac{\mathrm{15}}{\mathrm{2}} \\ $$$${t}^{\mathrm{3}} +{t}\leqslant\mathrm{30} \\ $$$${t}\left({t}^{\mathrm{2}} +\mathrm{1}\right)\leqslant\mathrm{30} \\ $$$$\Rightarrow{t}\leqslant\mathrm{3}\:\Rightarrow\left({x}+{y}\right)_{{max}} =\mathrm{3} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com