Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 185706 by Shrinava last updated on 26/Jan/23

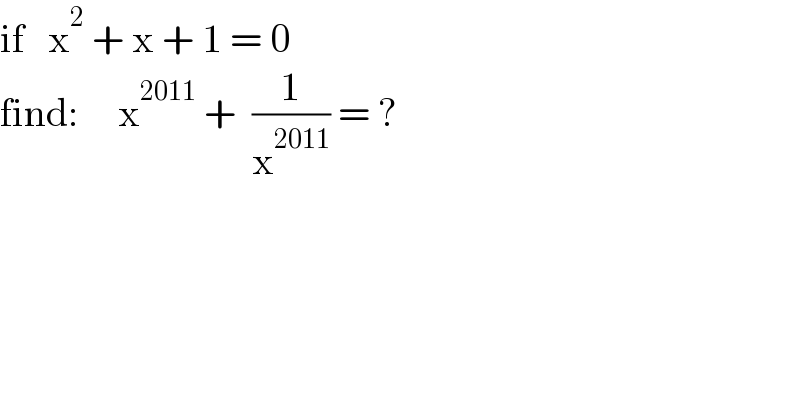
if x^2 + x + 1 = 0 find: x^(2011) + (1/x^(2011) ) = ?

$$\mathrm{if}\:\:\:\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{x}\:+\:\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{find}:\:\:\:\:\:\mathrm{x}^{\mathrm{2011}} \:+\:\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2011}} }\:=\:? \\ $$

Answered by Rajpurohith last updated on 26/Jan/23

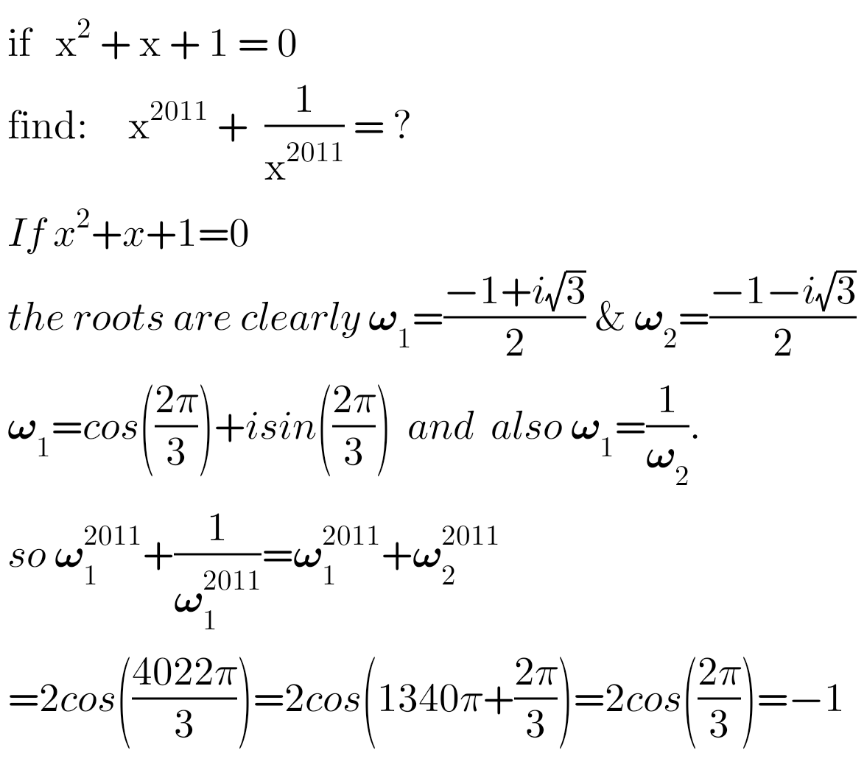
Answered by SEKRET last updated on 26/Jan/23

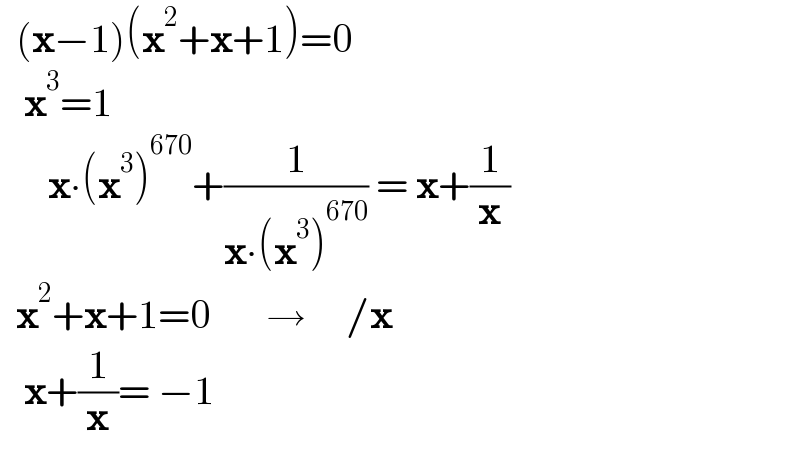
(x−1)(x^2 +x+1)=0 x^3 =1 x∙(x^3 )^(670) +(1/(x∙(x^3 )^(670) )) = x+(1/x) x^2 +x+1=0 → /x x+(1/x)= −1

$$\:\:\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{3}} =\mathrm{1} \\ $$$$\:\:\:\:\:\:\boldsymbol{\mathrm{x}}\centerdot\left(\boldsymbol{\mathrm{x}}^{\mathrm{3}} \right)^{\mathrm{670}} +\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}\centerdot\left(\boldsymbol{\mathrm{x}}^{\mathrm{3}} \right)^{\mathrm{670}} }\:=\:\boldsymbol{\mathrm{x}}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}} \\ $$$$\:\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}+\mathrm{1}=\mathrm{0}\:\:\:\:\:\:\:\rightarrow\:\:\:\:\:/\boldsymbol{\mathrm{x}} \\ $$$$\:\:\:\boldsymbol{\mathrm{x}}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}=\:−\mathrm{1}\: \\ $$

Answered by Rasheed.Sindhi last updated on 26/Jan/23

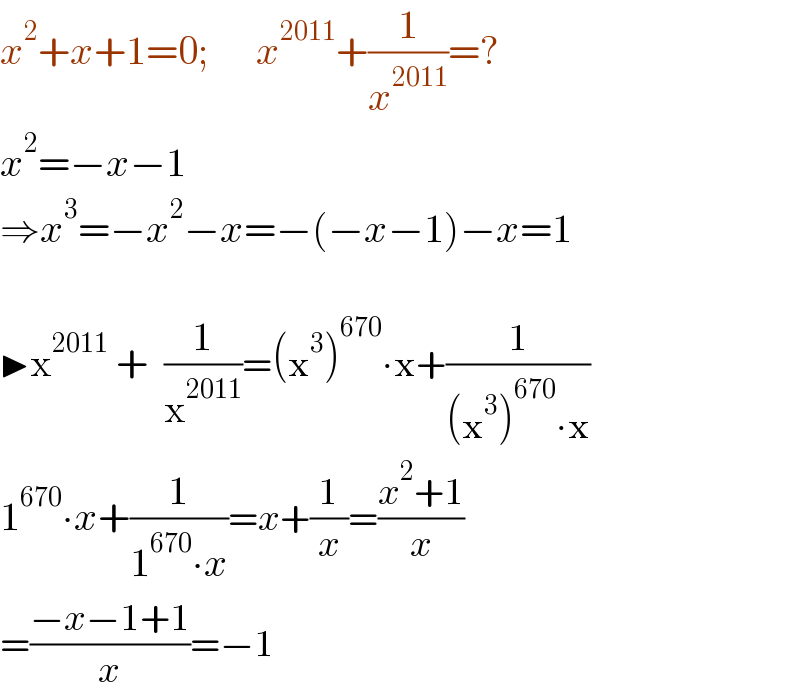
x^2 +x+1=0; x^(2011) +(1/x^(2011) )=? x^2 =−x−1 ⇒x^3 =−x^2 −x=−(−x−1)−x=1 ▶x^(2011) + (1/x^(2011) )=(x^3 )^(670) ∙x+(1/((x^3 )^(670) ∙x)) 1^(670) ∙x+(1/(1^(670) ∙x))=x+(1/x)=((x^2 +1)/x) =((−x−1+1)/x)=−1

$${x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0};\:\:\:\:\:\:{x}^{\mathrm{2011}} +\frac{\mathrm{1}}{{x}^{\mathrm{2011}} }=? \\ $$$${x}^{\mathrm{2}} =−{x}−\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{3}} =−{x}^{\mathrm{2}} −{x}=−\left(−{x}−\mathrm{1}\right)−{x}=\mathrm{1} \\ $$$$\: \\ $$$$\blacktriangleright\mathrm{x}^{\mathrm{2011}} \:+\:\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2011}} }=\left(\mathrm{x}^{\mathrm{3}} \right)^{\mathrm{670}} \centerdot\mathrm{x}+\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{3}} \right)^{\mathrm{670}} \centerdot\mathrm{x}} \\ $$$$\mathrm{1}^{\mathrm{670}} \centerdot{x}+\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{670}} \centerdot{x}}={x}+\frac{\mathrm{1}}{{x}}=\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}} \\ $$$$=\frac{−{x}−\mathrm{1}+\mathrm{1}}{{x}}=−\mathrm{1} \\ $$

Commented by Spillover last updated on 26/Jan/23

perfect

$${perfect} \\ $$

Commented by Rasheed.Sindhi last updated on 27/Jan/23

ThanX for compliment.

$$\mathcal{T}{han}\mathcal{X}\:{for}\:{compliment}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com