Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 191611 by vishal1234 last updated on 27/Apr/23

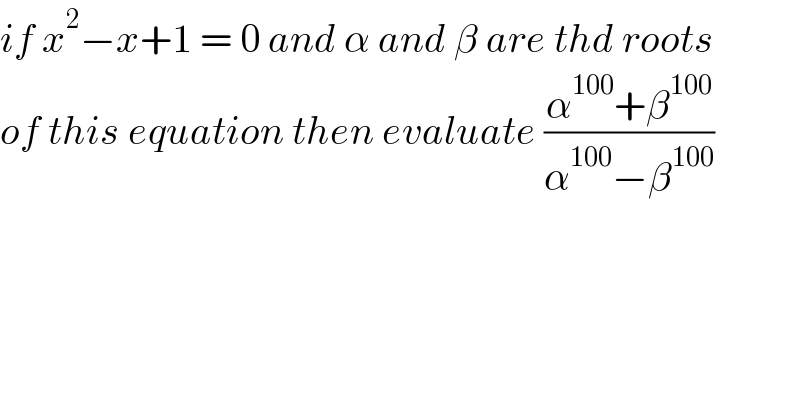
if x^2 −x+1 = 0 and α and β are thd roots of this equation then evaluate ((α^(100) +β^(100) )/(α^(100) −β^(100) ))

$${if}\:{x}^{\mathrm{2}} −{x}+\mathrm{1}\:=\:\mathrm{0}\:{and}\:\alpha\:{and}\:\beta\:{are}\:{thd}\:{roots} \\ $$$${of}\:{this}\:{equation}\:{then}\:{evaluate}\:\frac{\alpha^{\mathrm{100}} +\beta^{\mathrm{100}} }{\alpha^{\mathrm{100}} −\beta^{\mathrm{100}} } \\ $$

Answered by mehdee42 last updated on 27/Apr/23

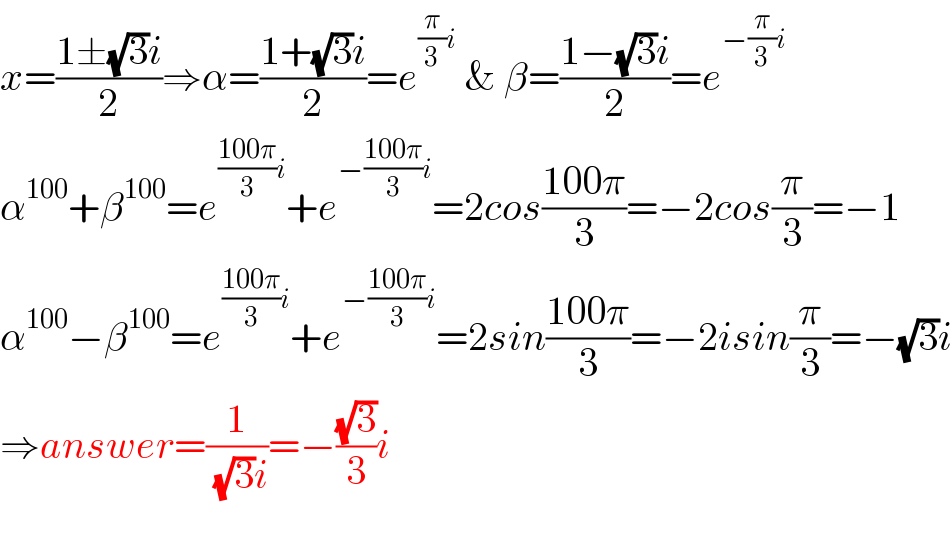
x=((1±(√3)i)/2)⇒α=((1+(√3)i)/2)=e^((π/3)i) & β=((1−(√3)i)/2)=e^(−(π/3)i) α^(100) +β^(100) =e^(((100π)/3)i) +e^(−((100π)/3)i) =2cos((100π)/3)=−2cos(π/3)=−1 α^(100) −β^(100) =e^(((100π)/3)i) +e^(−((100π)/3)i) =2sin((100π)/3)=−2isin(π/3)=−(√3)i ⇒answer=(1/( (√3)i))=−((√3)/3)i

$${x}=\frac{\mathrm{1}\pm\sqrt{\mathrm{3}}{i}}{\mathrm{2}}\Rightarrow\alpha=\frac{\mathrm{1}+\sqrt{\mathrm{3}}{i}}{\mathrm{2}}={e}^{\frac{\pi}{\mathrm{3}}{i}} \:\&\:\beta=\frac{\mathrm{1}−\sqrt{\mathrm{3}}{i}}{\mathrm{2}}={e}^{−\frac{\pi}{\mathrm{3}}{i}} \\ $$$$\alpha^{\mathrm{100}} +\beta^{\mathrm{100}} ={e}^{\frac{\mathrm{100}\pi}{\mathrm{3}}{i}} +{e}^{−\frac{\mathrm{100}\pi}{\mathrm{3}}{i}} =\mathrm{2}{cos}\frac{\mathrm{100}\pi}{\mathrm{3}}=−\mathrm{2}{cos}\frac{\pi}{\mathrm{3}}=−\mathrm{1} \\ $$$$\alpha^{\mathrm{100}} −\beta^{\mathrm{100}} ={e}^{\frac{\mathrm{100}\pi}{\mathrm{3}}{i}} +{e}^{−\frac{\mathrm{100}\pi}{\mathrm{3}}{i}} =\mathrm{2}{sin}\frac{\mathrm{100}\pi}{\mathrm{3}}=−\mathrm{2}{isin}\frac{\pi}{\mathrm{3}}=−\sqrt{\mathrm{3}}{i} \\ $$$$\Rightarrow{answer}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}{i}}=−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}{i} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com