Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 154385 by amin96 last updated on 17/Sep/21

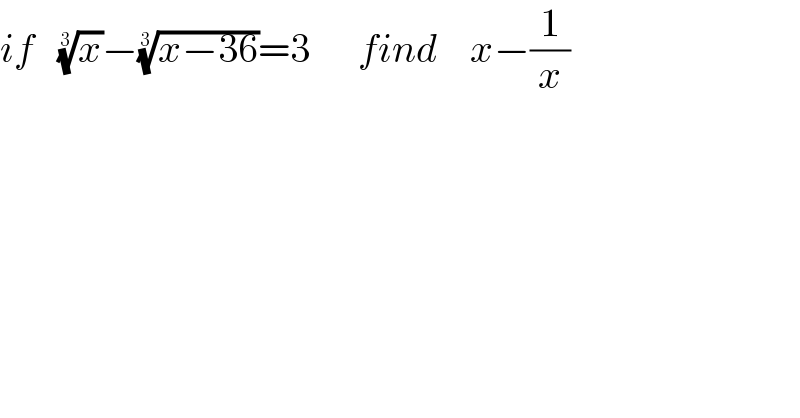
if (x)^(1/3) −((x−36))^(1/3) =3 find x−(1/x)

$${if}\:\:\:\sqrt[{\mathrm{3}}]{{x}}−\sqrt[{\mathrm{3}}]{{x}−\mathrm{36}}=\mathrm{3}\:\:\:\:\:\:{find}\:\:\:\:{x}−\frac{\mathrm{1}}{{x}} \\ $$

Answered by amin96 last updated on 18/Sep/21

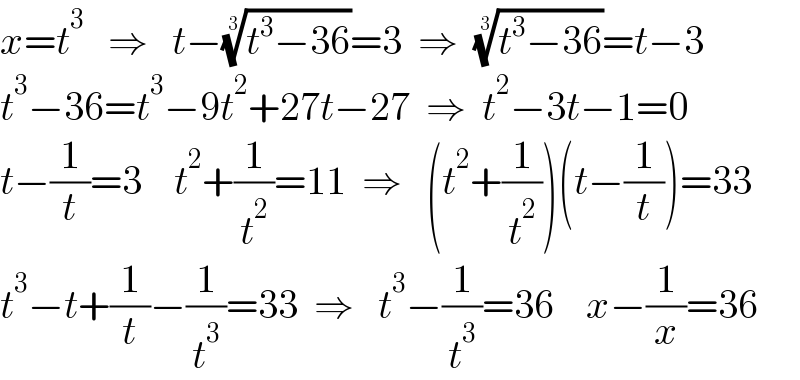
x=t^3 ⇒ t−((t^3 −36))^(1/3) =3 ⇒ ((t^3 −36))^(1/3) =t−3 t^3 −36=t^3 −9t^2 +27t−27 ⇒ t^2 −3t−1=0 t−(1/t)=3 t^2 +(1/t^2 )=11 ⇒ (t^2 +(1/t^2 ))(t−(1/t))=33 t^3 −t+(1/t)−(1/t^3 )=33 ⇒ t^3 −(1/t^3 )=36 x−(1/x)=36

$${x}={t}^{\mathrm{3}} \:\:\:\Rightarrow\:\:\:{t}−\sqrt[{\mathrm{3}}]{{t}^{\mathrm{3}} −\mathrm{36}}=\mathrm{3}\:\:\Rightarrow\:\:\sqrt[{\mathrm{3}}]{{t}^{\mathrm{3}} −\mathrm{36}}={t}−\mathrm{3} \\ $$$${t}^{\mathrm{3}} −\mathrm{36}={t}^{\mathrm{3}} −\mathrm{9}{t}^{\mathrm{2}} +\mathrm{27}{t}−\mathrm{27}\:\:\Rightarrow\:\:{t}^{\mathrm{2}} −\mathrm{3}{t}−\mathrm{1}=\mathrm{0} \\ $$$${t}−\frac{\mathrm{1}}{{t}}=\mathrm{3}\:\:\:\:{t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }=\mathrm{11}\:\:\Rightarrow\:\:\:\left({t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)\left({t}−\frac{\mathrm{1}}{{t}}\right)=\mathrm{33} \\ $$$${t}^{\mathrm{3}} −{t}+\frac{\mathrm{1}}{{t}}−\frac{\mathrm{1}}{{t}^{\mathrm{3}} }=\mathrm{33}\:\:\Rightarrow\:\:\:{t}^{\mathrm{3}} −\frac{\mathrm{1}}{{t}^{\mathrm{3}} }=\mathrm{36}\:\:\:\:{x}−\frac{\mathrm{1}}{{x}}=\mathrm{36} \\ $$

Answered by liberty last updated on 18/Sep/21

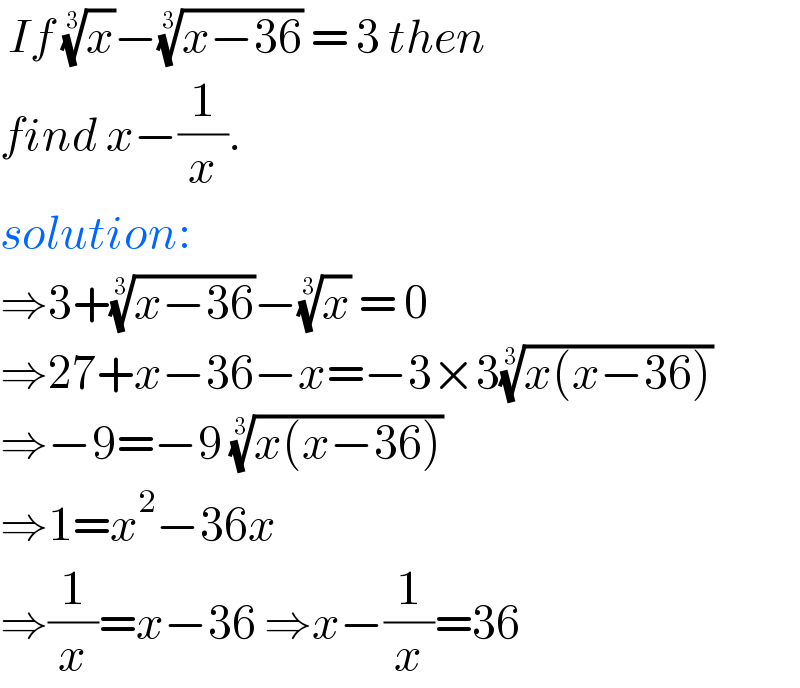
If (x)^(1/3) −((x−36))^(1/3) = 3 then find x−(1/x). solution: ⇒3+((x−36))^(1/3) −(x)^(1/3) = 0 ⇒27+x−36−x=−3×3((x(x−36)))^(1/3) ⇒−9=−9 ((x(x−36)))^(1/3) ⇒1=x^2 −36x ⇒(1/x)=x−36 ⇒x−(1/x)=36

$$\:{If}\:\sqrt[{\mathrm{3}}]{{x}}−\sqrt[{\mathrm{3}}]{{x}−\mathrm{36}}\:=\:\mathrm{3}\:{then} \\ $$$${find}\:{x}−\frac{\mathrm{1}}{{x}}. \\ $$$${solution}: \\ $$$$\Rightarrow\mathrm{3}+\sqrt[{\mathrm{3}}]{{x}−\mathrm{36}}−\sqrt[{\mathrm{3}}]{{x}}\:=\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{27}+{x}−\mathrm{36}−{x}=−\mathrm{3}×\mathrm{3}\sqrt[{\mathrm{3}}]{{x}\left({x}−\mathrm{36}\right)} \\ $$$$\Rightarrow−\mathrm{9}=−\mathrm{9}\:\sqrt[{\mathrm{3}}]{{x}\left({x}−\mathrm{36}\right)}\: \\ $$$$\Rightarrow\mathrm{1}={x}^{\mathrm{2}} −\mathrm{36}{x} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{x}}={x}−\mathrm{36}\:\Rightarrow{x}−\frac{\mathrm{1}}{{x}}=\mathrm{36} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com