Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 209837 by lmcp1203 last updated on 23/Jul/24

if the series Σ_(n=1) ^∞ (1/n^2 ) converges to k . find the convergence value of Σ_(n=1) ^∞ (1/((2n+1)^2 ))

$$ \\ $$$${if}\:{the}\:{series}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:{converges}\:{to}\:{k}\:.\:\:{find}\:\:{the}\:{convergence}\:{value}\:{of}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$

Answered by mr W last updated on 23/Jul/24

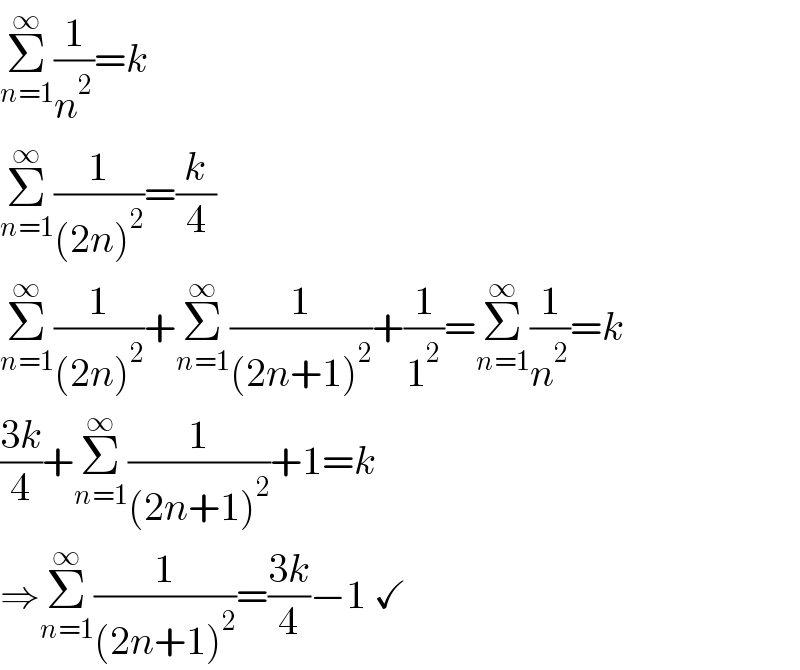
Σ_(n=1) ^∞ (1/n^2 )=k Σ_(n=1) ^∞ (1/((2n)^2 ))=(k/4) Σ_(n=1) ^∞ (1/((2n)^2 ))+Σ_(n=1) ^∞ (1/((2n+1)^2 ))+(1/1^2 )=Σ_(n=1) ^∞ (1/n^2 )=k ((3k)/4)+Σ_(n=1) ^∞ (1/((2n+1)^2 ))+1=k ⇒Σ_(n=1) ^∞ (1/((2n+1)^2 ))=((3k)/4)−1 ✓

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }={k} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)^{\mathrm{2}} }=\frac{{k}}{\mathrm{4}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)^{\mathrm{2}} }+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }={k} \\ $$$$\frac{\mathrm{3}{k}}{\mathrm{4}}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }+\mathrm{1}={k} \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{3}{k}}{\mathrm{4}}−\mathrm{1}\:\checkmark \\ $$

Answered by lmcp1203 last updated on 23/Jul/24

thanks

$${thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com