Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 188327 by HeferH last updated on 28/Feb/23

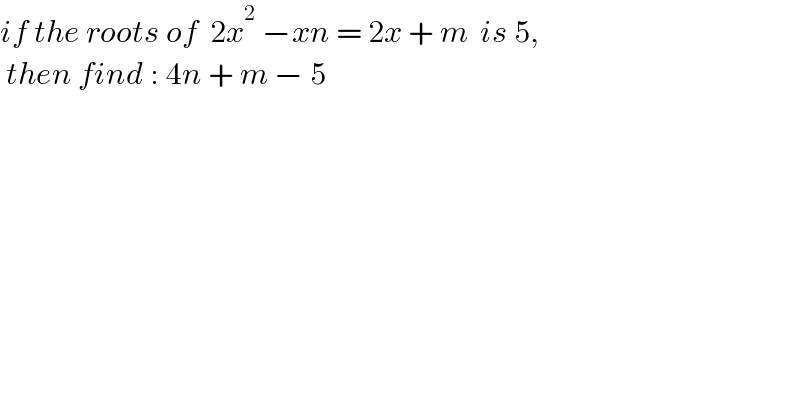
if the roots of 2x^2 −xn = 2x + m is 5, then find : 4n + m − 5

$${if}\:{the}\:{roots}\:{of}\:\:\mathrm{2}{x}^{\mathrm{2}} \:−{xn}\:=\:\mathrm{2}{x}\:+\:{m}\:\:{is}\:\mathrm{5}, \\ $$$$\:{then}\:{find}\::\:\mathrm{4}{n}\:+\:{m}\:−\:\mathrm{5}\: \\ $$$$\: \\ $$

Answered by Rasheed.Sindhi last updated on 28/Feb/23

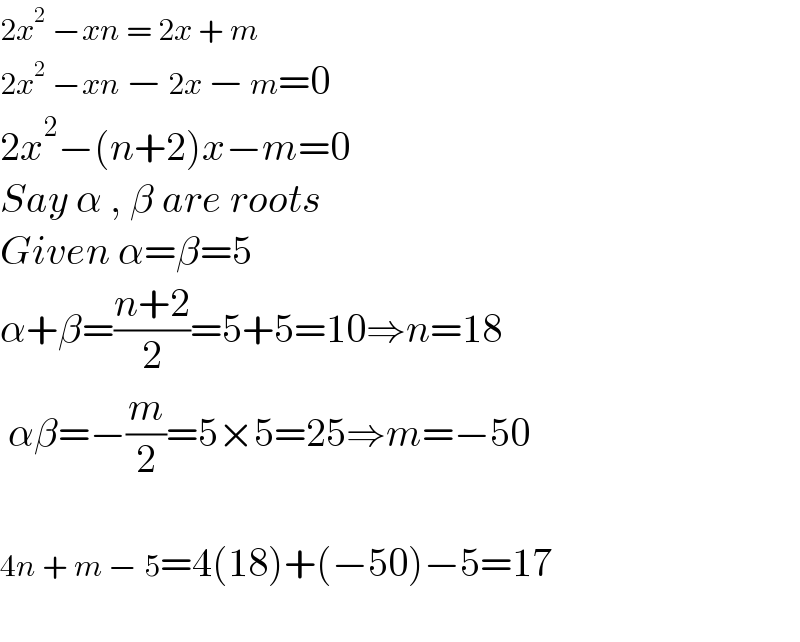
2x^2 −xn = 2x + m 2x^2 −xn − 2x − m=0 2x^2 −(n+2)x−m=0 Say α , β are roots Given α=β=5 α+β=((n+2)/2)=5+5=10⇒n=18 αβ=−(m/2)=5×5=25⇒m=−50 4n + m − 5=4(18)+(−50)−5=17

$$\mathrm{2}{x}^{\mathrm{2}} \:−{xn}\:=\:\mathrm{2}{x}\:+\:{m} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} \:−{xn}\:−\:\mathrm{2}{x}\:−\:{m}=\mathrm{0} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} −\left({n}+\mathrm{2}\right){x}−{m}=\mathrm{0} \\ $$$${Say}\:\alpha\:,\:\beta\:{are}\:{roots} \\ $$$${Given}\:\alpha=\beta=\mathrm{5} \\ $$$$\alpha+\beta=\frac{{n}+\mathrm{2}}{\mathrm{2}}=\mathrm{5}+\mathrm{5}=\mathrm{10}\Rightarrow{n}=\mathrm{18} \\ $$$$\:\alpha\beta=−\frac{{m}}{\mathrm{2}}=\mathrm{5}×\mathrm{5}=\mathrm{25}\Rightarrow{m}=−\mathrm{50} \\ $$$$ \\ $$$$\mathrm{4}{n}\:+\:{m}\:−\:\mathrm{5}=\mathrm{4}\left(\mathrm{18}\right)+\left(−\mathrm{50}\right)−\mathrm{5}=\mathrm{17} \\ $$$$ \\ $$

Commented by HeferH last updated on 28/Feb/23

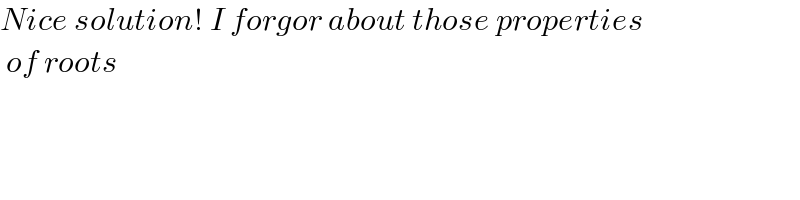
Nice solution! I forgor about those properties of roots

$${Nice}\:{solution}!\:{I}\:{forgor}\:{about}\:{those}\:{properties} \\ $$$$\:{of}\:{roots} \\ $$

Answered by Rasheed.Sindhi last updated on 28/Feb/23

Another way... 2x^2 −xn = 2x + m 2x^2 −xn−2x− m=0 2x^2 −(n+2)x−m=0....(i) The equation having roots 5 , 5 is (x−5)^2 =0 x^2 −10x+25=0.........(ii) Comparing coefficients of (i) & (ii) (2/1)=((−(n+2))/(−10))=(( −m )/(25)) n+2=20 ∧ −m=50 n=18 ∧ m=−50 ▶ 4n + m − 5=4(18)+(−50)−5=17

$${Another}\:{way}... \\ $$$$\:\mathrm{2}{x}^{\mathrm{2}} \:−{xn}\:=\:\mathrm{2}{x}\:+\:{m} \\ $$$$\:\mathrm{2}{x}^{\mathrm{2}} \:−{xn}−\mathrm{2}{x}−\:{m}=\mathrm{0} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} −\left({n}+\mathrm{2}\right){x}−{m}=\mathrm{0}....\left({i}\right) \\ $$$${The}\:{equation}\:{having}\:{roots}\:\mathrm{5}\:,\:\mathrm{5}\:{is} \\ $$$$\:\:\:\:\left({x}−\mathrm{5}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{25}=\mathrm{0}.........\left({ii}\right) \\ $$$${Comparing}\:{coefficients}\:{of}\:\left({i}\right)\:\&\:\left({ii}\right) \\ $$$$\frac{\mathrm{2}}{\mathrm{1}}=\frac{−\left({n}+\mathrm{2}\right)}{−\mathrm{10}}=\frac{\:−{m}\:}{\mathrm{25}} \\ $$$${n}+\mathrm{2}=\mathrm{20}\:\wedge\:−{m}=\mathrm{50} \\ $$$$\:\:\:{n}=\mathrm{18}\:\wedge\:{m}=−\mathrm{50} \\ $$$$\blacktriangleright\:\mathrm{4}{n}\:+\:{m}\:−\:\mathrm{5}=\mathrm{4}\left(\mathrm{18}\right)+\left(−\mathrm{50}\right)−\mathrm{5}=\mathrm{17} \\ $$

Answered by Rasheed.Sindhi last updated on 28/Feb/23

2x^2 −(n+2)x−m=0 • ∵5 is root ∴2(5)^2 −(n+2)(5)−m=0 50−5n−10−m=0 m+5n=40..........(i) •(d/dx)(2x^2 −(n+2)x−m)_(n=5) =(d/dx)(0)_(x=5) 4x−(n+2)]_(x=5) =0 ⇒4(5)−n−2=0 ⇒n=18 (i)⇒m+5(18)=40⇒m=−50 ▶4n + m − 5=4(18)+(−50)−5=17

$$\mathrm{2}{x}^{\mathrm{2}} −\left({n}+\mathrm{2}\right){x}−{m}=\mathrm{0} \\ $$$$\bullet\:\because\mathrm{5}\:{is}\:{root} \\ $$$$\:\:\:\therefore\mathrm{2}\left(\mathrm{5}\right)^{\mathrm{2}} −\left({n}+\mathrm{2}\right)\left(\mathrm{5}\right)−{m}=\mathrm{0} \\ $$$$\:\:\:\:\mathrm{50}−\mathrm{5}{n}−\mathrm{10}−{m}=\mathrm{0} \\ $$$$\:\:\:\:{m}+\mathrm{5}{n}=\mathrm{40}..........\left({i}\right) \\ $$$$\bullet\frac{{d}}{{dx}}\left(\mathrm{2}{x}^{\mathrm{2}} −\left({n}+\mathrm{2}\right){x}−{m}\right)_{{n}=\mathrm{5}} =\frac{{d}}{{dx}}\left(\mathrm{0}\right)_{{x}=\mathrm{5}} \\ $$$$\left.\:\:\mathrm{4}{x}−\left({n}+\mathrm{2}\right)\right]_{{x}=\mathrm{5}} =\mathrm{0} \\ $$$$\:\:\Rightarrow\mathrm{4}\left(\mathrm{5}\right)−{n}−\mathrm{2}=\mathrm{0} \\ $$$$\:\:\Rightarrow{n}=\mathrm{18} \\ $$$$\:\:\:\left({i}\right)\Rightarrow{m}+\mathrm{5}\left(\mathrm{18}\right)=\mathrm{40}\Rightarrow{m}=−\mathrm{50} \\ $$$$\blacktriangleright\mathrm{4}{n}\:+\:{m}\:−\:\mathrm{5}=\mathrm{4}\left(\mathrm{18}\right)+\left(−\mathrm{50}\right)−\mathrm{5}=\mathrm{17}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com