Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 188320 by normans last updated on 27/Feb/23

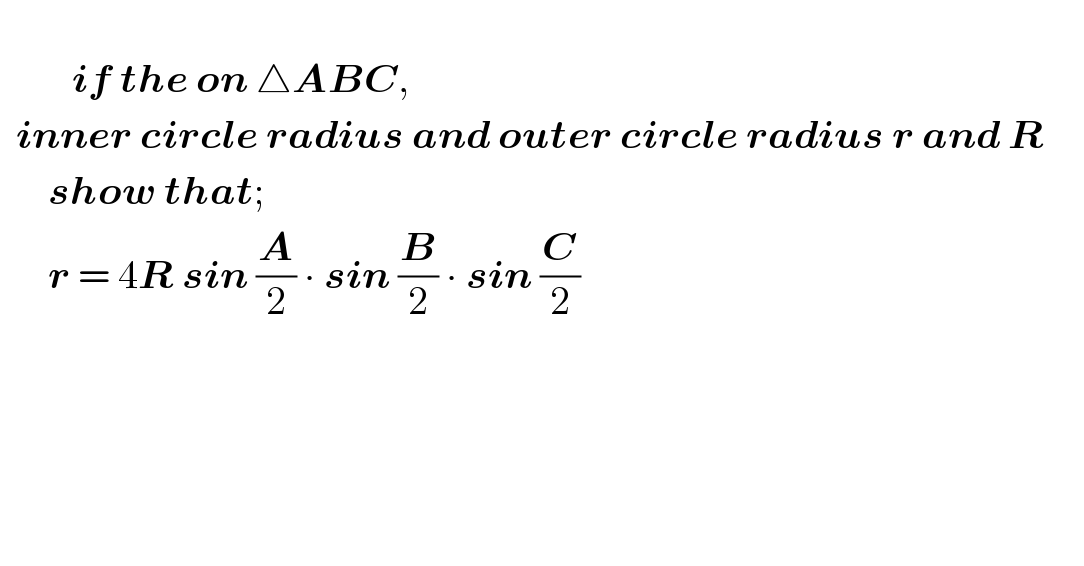
if the on △ABC, inner circle radius and outer circle radius r and R show that; r = 4R sin (A/2) ∙ sin (B/2) ∙ sin (C/2)

$$ \\ $$$$\:\:\:\:\:\:\:\:\:\boldsymbol{{if}}\:\boldsymbol{{the}}\:\boldsymbol{{on}}\:\bigtriangleup\boldsymbol{{ABC}},\: \\ $$$$\:\:\boldsymbol{{inner}}\:\boldsymbol{{circle}}\:\boldsymbol{{radius}}\:\boldsymbol{{and}}\:\boldsymbol{{outer}}\:\boldsymbol{{circle}}\:\boldsymbol{{radius}}\:\boldsymbol{{r}}\:\boldsymbol{{and}}\:\boldsymbol{{R}}\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\boldsymbol{{show}}\:\boldsymbol{{that}}; \\ $$$$\:\:\:\:\:\:\boldsymbol{{r}}\:=\:\mathrm{4}\boldsymbol{{R}}\:\boldsymbol{{sin}}\:\frac{\boldsymbol{{A}}}{\mathrm{2}}\:\centerdot\:\boldsymbol{{sin}}\:\frac{\boldsymbol{{B}}}{\mathrm{2}}\:\centerdot\:\boldsymbol{{sin}}\:\frac{\boldsymbol{{C}}}{\mathrm{2}} \\ $$$$ \\ $$

Answered by mr W last updated on 28/Feb/23

(a/(sin A))=(b/(sin B))=(c/(sin C))=2R Δ=((abc)/(4R))=2R^2 sin A sin B sin C r=((2Δ)/(a+b+c)) =((2Δ)/(2R(sin A+sin B+sin C))) =((2R^2 sin A sin B sin C)/(R(sin A+sin B+sin C))) =((2R sin A sin B sin C)/(sin A+sin B+sin C)) =((2R sin A sin B sin C)/(4 cos (A/2) cos (B/2) cos (C/2))) =((16R sin (A/2) cos (A/2) sin (B/2) cos (B/2) sin (C/2) cos (C/2))/(4 cos (A/2) cos (B/2) cos (C/2))) =4R sin (A/2) sin (B/2) sin (C/2)

$$\frac{{a}}{\mathrm{sin}\:{A}}=\frac{{b}}{\mathrm{sin}\:{B}}=\frac{{c}}{\mathrm{sin}\:{C}}=\mathrm{2}{R} \\ $$$$\Delta=\frac{{abc}}{\mathrm{4}{R}}=\mathrm{2}{R}^{\mathrm{2}} \:\mathrm{sin}\:{A}\:\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C} \\ $$$${r}=\frac{\mathrm{2}\Delta}{{a}+{b}+{c}} \\ $$$$\:\:=\frac{\mathrm{2}\Delta}{\mathrm{2}{R}\left(\mathrm{sin}\:{A}+\mathrm{sin}\:{B}+\mathrm{sin}\:{C}\right)} \\ $$$$\:\:=\frac{\mathrm{2}{R}^{\mathrm{2}} \:\mathrm{sin}\:{A}\:\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}}{{R}\left(\mathrm{sin}\:{A}+\mathrm{sin}\:{B}+\mathrm{sin}\:{C}\right)} \\ $$$$\:\:=\frac{\mathrm{2}{R}\:\mathrm{sin}\:{A}\:\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}}{\mathrm{sin}\:{A}+\mathrm{sin}\:{B}+\mathrm{sin}\:{C}} \\ $$$$\:\:=\frac{\mathrm{2}{R}\:\mathrm{sin}\:{A}\:\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}}{\mathrm{4}\:\mathrm{cos}\:\frac{{A}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{C}}{\mathrm{2}}} \\ $$$$\:\:=\frac{\mathrm{16}{R}\:\mathrm{sin}\:\frac{{A}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{A}}{\mathrm{2}}\:\:\mathrm{sin}\:\frac{{B}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{C}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{C}}{\mathrm{2}}}{\mathrm{4}\:\mathrm{cos}\:\frac{{A}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{C}}{\mathrm{2}}} \\ $$$$\:\:=\mathrm{4}{R}\:\mathrm{sin}\:\frac{{A}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{B}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{C}}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com