Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 172124 by Mikenice last updated on 23/Jun/22

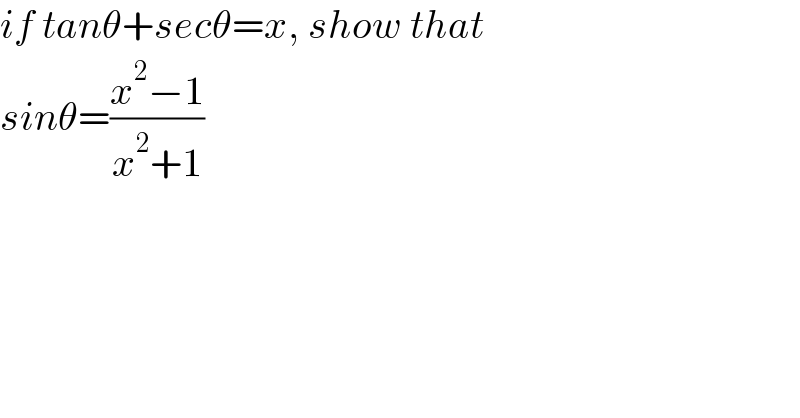
if tanθ+secθ=x, show that sinθ=((x^2 −1)/(x^2 +1))

$${if}\:{tan}\theta+{sec}\theta={x},\:{show}\:{that}\: \\ $$$${sin}\theta=\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$

Commented by infinityaction last updated on 23/Jun/22

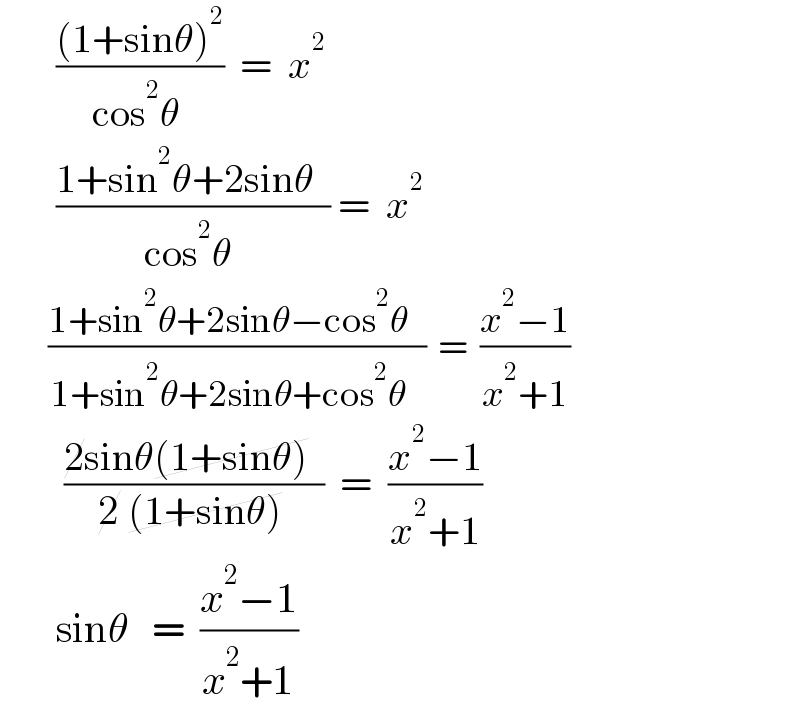
(((1+sinθ)^2 )/(cos^2 θ )) = x^2 ((1+sin^2 θ+2sinθ )/(cos^2 θ )) = x^2 ((1+sin^2 θ+2sinθ−cos^2 θ )/(1+sin^2 θ+2sinθ+cos^2 θ )) = ((x^2 −1)/(x^2 +1)) ((2sinθ(1+sinθ) )/(2 (1+sinθ) )) = ((x^2 −1)/(x^2 +1)) sinθ = ((x^2 −1)/(x^2 +1))

$$\:\:\:\:\:\:\:\frac{\left(\mathrm{1}+\mathrm{sin}\theta\right)^{\mathrm{2}} }{\mathrm{cos}^{\mathrm{2}} \theta\:}\:\:=\:\:{x}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \theta+\mathrm{2sin}\theta\:\:}{\mathrm{cos}^{\mathrm{2}} \theta\:}\:=\:\:{x}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\frac{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \theta+\mathrm{2sin}\theta−\mathrm{cos}^{\mathrm{2}} \theta\:\:\:}{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \theta+\mathrm{2sin}\theta+\mathrm{cos}^{\mathrm{2}} \theta\:\:\:}\:\:=\:\:\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\frac{\cancel{\mathrm{2}sin}\theta\cancel{\left(\mathrm{1}+\mathrm{sin}\theta\right)}\:\:}{\cancel{\mathrm{2}}\:\cancel{\left(\mathrm{1}+\mathrm{sin}\theta\right)}\:}\:\:=\:\:\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\mathrm{sin}\theta\:\:\:=\:\:\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}\: \\ $$

Commented by BaliramSingh last updated on 24/Jun/22

Nice Solution

$${Nice}\:{Solution} \\ $$

Answered by BaliramSingh last updated on 23/Jun/22

secθ+tanθ=x ..... .....[1] (((secθ+tanθ)(secθ−tanθ))/((secθ−tanθ))) = x ((sec^2 θ−tan^2 θ)/((secθ−tanθ))) = x (1/((secθ−tanθ)))=x secθ−tanθ = (1/x) ...........[2] by [1]+[2] 2secθ=x+(1/x) ............[3] by [1]−[2] 2tanθ=x−(1/x) .............[4] by [4]÷[3] ((2tanθ)/(2secθ)) = ((x−(1/x))/(x+(1/x))) (((sinθ)/(cosθ))/(1/(cosθ))) = (((x^2 −1)/x)/((x^2 +1)/x)) sinθ = ((x^2 −1)/(x^2 +1))

$$ \\ $$$${sec}\theta+{tan}\theta={x}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.....\:.....\left[\mathrm{1}\right] \\ $$$$\frac{\left({sec}\theta+{tan}\theta\right)\left({sec}\theta−{tan}\theta\right)}{\left({sec}\theta−{tan}\theta\right)}\:=\:{x} \\ $$$$\frac{{sec}^{\mathrm{2}} \theta−{tan}^{\mathrm{2}} \theta}{\left({sec}\theta−{tan}\theta\right)}\:=\:{x} \\ $$$$\frac{\mathrm{1}}{\left({sec}\theta−{tan}\theta\right)}={x}\:\:\:\:\:\:\:\:\:\: \\ $$$${sec}\theta−{tan}\theta\:=\:\frac{\mathrm{1}}{{x}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...........\left[\mathrm{2}\right] \\ $$$$\:\:\:{by}\:\:\:\:\left[\mathrm{1}\right]+\left[\mathrm{2}\right] \\ $$$$\mathrm{2}{sec}\theta={x}+\frac{\mathrm{1}}{{x}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:............\left[\mathrm{3}\right] \\ $$$$\:\:\:{by}\:\:\:\:\left[\mathrm{1}\right]−\left[\mathrm{2}\right] \\ $$$$\mathrm{2}{tan}\theta={x}−\frac{\mathrm{1}}{{x}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.............\left[\mathrm{4}\right] \\ $$$${by}\:\:\:\:\:\left[\mathrm{4}\right]\boldsymbol{\div}\left[\mathrm{3}\right] \\ $$$$\:\frac{\mathrm{2}{tan}\theta}{\mathrm{2}{sec}\theta}\:=\:\frac{{x}−\frac{\mathrm{1}}{{x}}}{{x}+\frac{\mathrm{1}}{{x}}} \\ $$$$\frac{\frac{{sin}\theta}{{cos}\theta}}{\frac{\mathrm{1}}{{cos}\theta}}\:=\:\frac{\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}}}{\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}}} \\ $$$${sin}\theta\:=\:\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$ \\ $$

Commented by peter frank last updated on 23/Jun/22

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Answered by Plato last updated on 23/Jun/22

soln sin θ=((x^2 −1)/(x^2 +1)) ((x^2 −1)/(x^2 +1)) (((tan θ+sec θ)^2 −1)/((tan θ+sec θ)^2 +1)) ((tan^2 θ+sec^2 θ+2tan θsec θ−1)/(tan^2 θ+sec^2 θ+2tan θsec θ+1)) but 1+tan^2 θ=sec^2 θ ((2tan θsec θ+2tan^2 θ)/(2tan θsec θ+2tan^2 θ+2)) factoring 2 ((tanθ secθ+tan^2 θ )/(tan θsec θ+sec^2 θ)) divide by secθ ((tanθ+tan^2 θcos θ)/(tanθ+(1/(cos θ)))) ((((sinθ)/(cosθ))+((sin^2 θ)/(cosθ)))/( ((sinθ )/(cosθ ))+(1/(cosθ)))) (((sinθ(1+sinθ))/(cosθ))/((1+sinθ)/(cosθ))) ((sinθ(1+sinθ))/((1+sinθ))) =sin θ

$${soln} \\ $$$$\mathrm{sin}\:\theta=\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\frac{\left(\mathrm{tan}\:\theta+\mathrm{sec}\:\theta\right)^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{tan}\:\theta+\mathrm{sec}\:\theta\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$\frac{\mathrm{tan}\:^{\mathrm{2}} \theta+\mathrm{sec}\:^{\mathrm{2}} \theta+\mathrm{2tan}\:\theta\mathrm{sec}\:\theta−\mathrm{1}}{\mathrm{tan}\:^{\mathrm{2}} \theta+\mathrm{sec}\:^{\mathrm{2}} \theta+\mathrm{2tan}\:\theta\mathrm{sec}\:\theta+\mathrm{1}} \\ $$$${but}\:\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta=\mathrm{sec}\:^{\mathrm{2}} \theta \\ $$$$\frac{\mathrm{2tan}\:\theta\mathrm{sec}\:\theta+\mathrm{2tan}^{\mathrm{2}} \theta}{\mathrm{2tan}\:\theta\mathrm{sec}\:\theta+\mathrm{2tan}\:^{\mathrm{2}} \theta+\mathrm{2}} \\ $$$${factoring}\:\mathrm{2}\:\: \\ $$$$\frac{\mathrm{tan}\theta\:\mathrm{sec}\theta+\mathrm{tan}^{\mathrm{2}} \theta\:}{\mathrm{tan}\:\theta\mathrm{sec}\:\theta+\mathrm{sec}^{\mathrm{2}} \theta} \\ $$$${divide}\:{by}\:\mathrm{sec}\theta \\ $$$$\frac{\mathrm{tan}\theta+\mathrm{tan}^{\mathrm{2}} \theta\mathrm{cos}\:\theta}{\mathrm{tan}\theta+\frac{\mathrm{1}}{\mathrm{cos}\:\theta}} \\ $$$$\frac{\frac{\mathrm{sin}\theta}{\mathrm{cos}\theta}+\frac{\mathrm{sin}^{\mathrm{2}} \theta}{\mathrm{cos}\theta}}{\:\frac{\mathrm{sin}\theta\:}{\mathrm{cos}\theta\:}+\frac{\mathrm{1}}{\mathrm{cos}\theta}} \\ $$$$\frac{\frac{\mathrm{sin}\theta\left(\mathrm{1}+\mathrm{sin}\theta\right)}{\mathrm{cos}\theta}}{\frac{\mathrm{1}+\mathrm{sin}\theta}{\mathrm{cos}\theta}} \\ $$$$\frac{\mathrm{sin}\theta\left(\mathrm{1}+\mathrm{sin}\theta\right)}{\left(\mathrm{1}+\mathrm{sin}\theta\right)} \\ $$$$=\mathrm{sin}\:\theta \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com