Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 191344 by mnjuly1970 last updated on 23/Apr/23

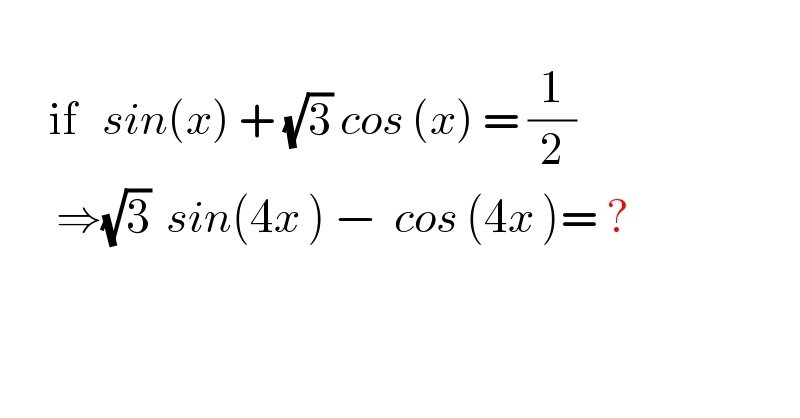
if sin(x) + (√3) cos (x) = (1/2) ⇒(√3) sin(4x ) − cos (4x )= ?

$$ \\ $$$$\:\:\:\:\:\:\mathrm{if}\:\:\:{sin}\left({x}\right)\:+\:\sqrt{\mathrm{3}}\:{cos}\:\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\Rightarrow\sqrt{\mathrm{3}}\:\:{sin}\left(\mathrm{4}{x}\:\right)\:−\:\:{cos}\:\left(\mathrm{4}{x}\:\right)=\:? \\ $$$$ \\ $$

Answered by mehdee42 last updated on 23/Apr/23

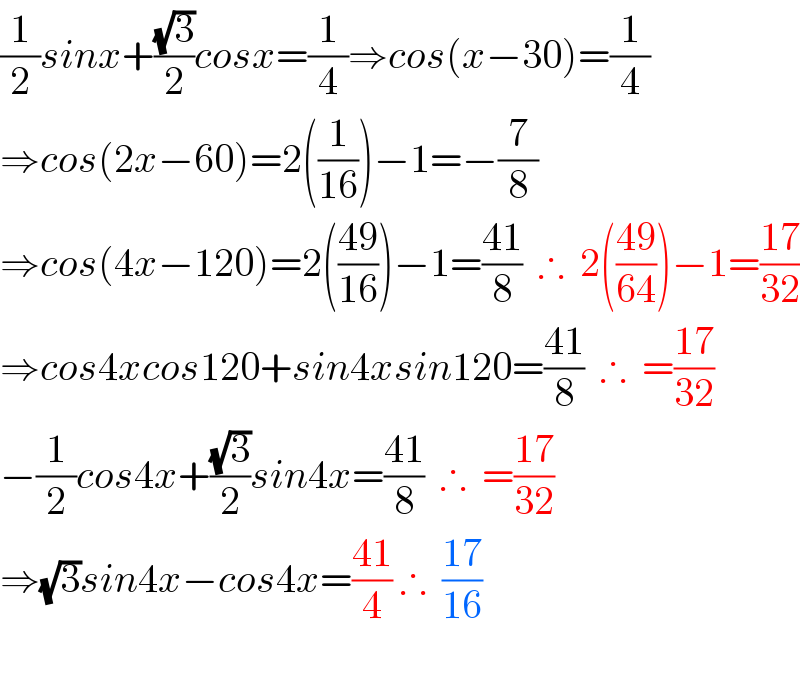
(1/2)sinx+((√3)/2)cosx=(1/4)⇒cos(x−30)=(1/4) ⇒cos(2x−60)=2((1/(16)))−1=−(7/8) ⇒cos(4x−120)=2(((49)/(16)))−1=((41)/8) ∴ 2(((49)/(64)))−1=((17)/(32)) ⇒cos4xcos120+sin4xsin120=((41)/8) ∴ =((17)/(32)) −(1/2)cos4x+((√3)/2)sin4x=((41)/8) ∴ =((17)/(32)) ⇒(√3)sin4x−cos4x=((41)/4) ∴ ((17)/(16))

$$\frac{\mathrm{1}}{\mathrm{2}}{sinx}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{cosx}=\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow{cos}\left({x}−\mathrm{30}\right)=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{cos}\left(\mathrm{2}{x}−\mathrm{60}\right)=\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{16}}\right)−\mathrm{1}=−\frac{\mathrm{7}}{\mathrm{8}} \\ $$$$\Rightarrow{cos}\left(\mathrm{4}{x}−\mathrm{120}\right)=\mathrm{2}\left(\frac{\mathrm{49}}{\mathrm{16}}\right)−\mathrm{1}=\frac{\mathrm{41}}{\mathrm{8}}\:\:\therefore\:\:\mathrm{2}\left(\frac{\mathrm{49}}{\mathrm{64}}\right)−\mathrm{1}=\frac{\mathrm{17}}{\mathrm{32}} \\ $$$$\Rightarrow{cos}\mathrm{4}{xcos}\mathrm{120}+{sin}\mathrm{4}{xsin}\mathrm{120}=\frac{\mathrm{41}}{\mathrm{8}}\:\:\therefore\:\:=\frac{\mathrm{17}}{\mathrm{32}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}{cos}\mathrm{4}{x}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sin}\mathrm{4}{x}=\frac{\mathrm{41}}{\mathrm{8}}\:\:\therefore\:\:=\frac{\mathrm{17}}{\mathrm{32}} \\ $$$$\Rightarrow\sqrt{\mathrm{3}}{sin}\mathrm{4}{x}−{cos}\mathrm{4}{x}=\frac{\mathrm{41}}{\mathrm{4}}\:\therefore\:\:\frac{\mathrm{17}}{\mathrm{16}} \\ $$$$ \\ $$

Commented by mr W last updated on 23/Apr/23

very nice sir!

$${very}\:{nice}\:{sir}! \\ $$

Commented by mehdee42 last updated on 23/Apr/23

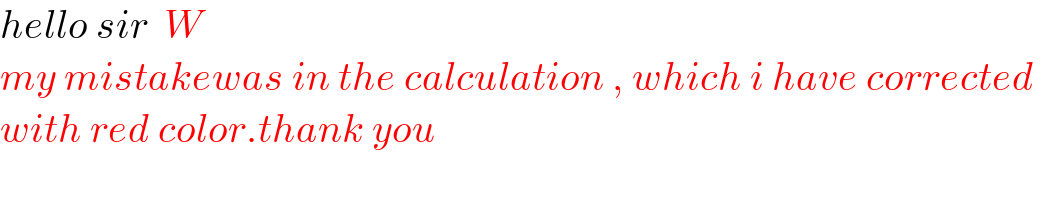
hello sir W my mistakewas in the calculation , which i have corrected with red color.thank you

$${hello}\:{sir}\:\:{W} \\ $$$${my}\:{mistakewas}\:{in}\:{the}\:{calculation}\:,\:{which}\:{i}\:{have}\:{corrected}\: \\ $$$${with}\:{red}\:{color}.{thank}\:{you} \\ $$

Answered by mr W last updated on 23/Apr/23

((sin x)/2)+((√3)/2) cos x=(1/4) sin x sin (π/6)+cos x cos (π/6)=(1/4) cos (x−(π/6))=(1/4) ⇒x−(π/6)=2kπ±cos^(−1) (1/4) ⇒x=2kπ+(π/6)±cos^(−1) (1/4) (√3) sin 4x−cos 4x =2(sin 4x cos (π/6)−cos 4x sin (π/6)) =2 sin (4x−(π/6)) =2 sin (8kπ+(π/2)±4 cos^(−1) (1/4)) =2 cos (4 cos^(−1) (1/4)) =2 [2 cos^2 (2 cos^(−1) (1/4))−1] =2 [2 {2 cos^2 (cos^(−1) (1/4))−1}^2 −1] =2 [2 {2×(1/4^2 )−1}^2 −1] =2 [2 {(7/8)}^2 −1] =((17)/(16)) ✓

$$\frac{\mathrm{sin}\:{x}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{cos}\:{x}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{sin}\:{x}\:\mathrm{sin}\:\frac{\pi}{\mathrm{6}}+\mathrm{cos}\:{x}\:\mathrm{cos}\:\frac{\pi}{\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{cos}\:\left({x}−\frac{\pi}{\mathrm{6}}\right)=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{x}−\frac{\pi}{\mathrm{6}}=\mathrm{2}{k}\pi\pm\mathrm{cos}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{x}=\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{6}}\pm\mathrm{cos}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$ \\ $$$$\sqrt{\mathrm{3}}\:\mathrm{sin}\:\mathrm{4}{x}−\mathrm{cos}\:\mathrm{4}{x} \\ $$$$=\mathrm{2}\left(\mathrm{sin}\:\mathrm{4}{x}\:\mathrm{cos}\:\frac{\pi}{\mathrm{6}}−\mathrm{cos}\:\mathrm{4}{x}\:\mathrm{sin}\:\frac{\pi}{\mathrm{6}}\right) \\ $$$$=\mathrm{2}\:\mathrm{sin}\:\left(\mathrm{4}{x}−\frac{\pi}{\mathrm{6}}\right) \\ $$$$=\mathrm{2}\:\mathrm{sin}\:\left(\mathrm{8}{k}\pi+\frac{\pi}{\mathrm{2}}\pm\mathrm{4}\:\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$=\mathrm{2}\:\mathrm{cos}\:\left(\mathrm{4}\:\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$=\mathrm{2}\:\left[\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\left(\mathrm{2}\:\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{4}}\right)−\mathrm{1}\right] \\ $$$$=\mathrm{2}\:\left[\mathrm{2}\:\left\{\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\:\left(\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{4}}\right)−\mathrm{1}\right\}^{\mathrm{2}} −\mathrm{1}\right] \\ $$$$=\mathrm{2}\:\left[\mathrm{2}\:\left\{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} }−\mathrm{1}\right\}^{\mathrm{2}} −\mathrm{1}\right] \\ $$$$=\mathrm{2}\:\left[\mathrm{2}\:\left\{\frac{\mathrm{7}}{\mathrm{8}}\right\}^{\mathrm{2}} −\mathrm{1}\right] \\ $$$$=\frac{\mathrm{17}}{\mathrm{16}}\:\checkmark \\ $$

Commented by mnjuly1970 last updated on 23/Apr/23

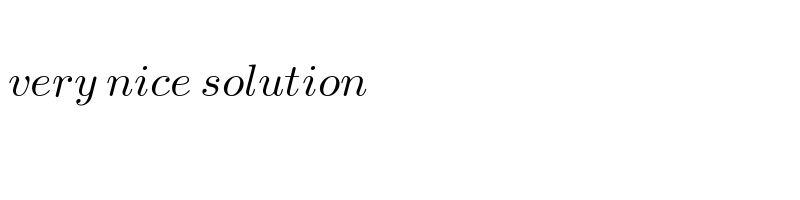
very nice solution

$$\:{very}\:{nice}\:{solution}\:\: \\ $$

Answered by cortano12 last updated on 23/Apr/23

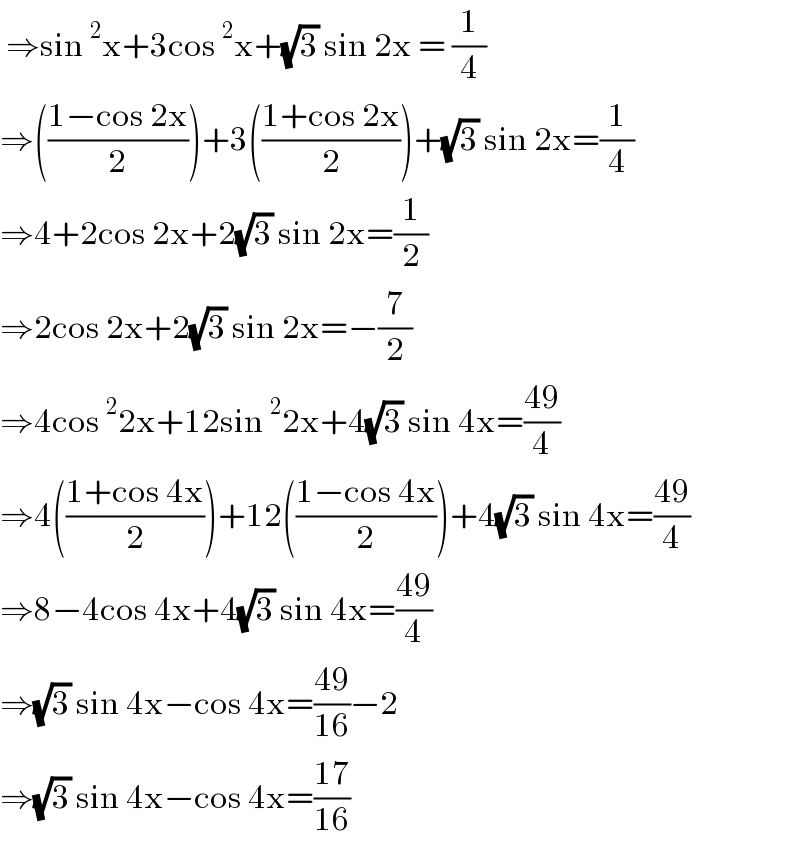
⇒sin^2 x+3cos^2 x+(√3) sin 2x = (1/4) ⇒(((1−cos 2x)/2))+3(((1+cos 2x)/2))+(√3) sin 2x=(1/4) ⇒4+2cos 2x+2(√3) sin 2x=(1/2) ⇒2cos 2x+2(√3) sin 2x=−(7/2) ⇒4cos^2 2x+12sin^2 2x+4(√3) sin 4x=((49)/4) ⇒4(((1+cos 4x)/2))+12(((1−cos 4x)/2))+4(√3) sin 4x=((49)/4) ⇒8−4cos 4x+4(√3) sin 4x=((49)/4) ⇒(√3) sin 4x−cos 4x=((49)/(16))−2 ⇒(√3) sin 4x−cos 4x=((17)/(16))

$$\:\Rightarrow\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{3cos}\:^{\mathrm{2}} \mathrm{x}+\sqrt{\mathrm{3}}\:\mathrm{sin}\:\mathrm{2x}\:=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\left(\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2x}}{\mathrm{2}}\right)+\mathrm{3}\left(\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2x}}{\mathrm{2}}\right)+\sqrt{\mathrm{3}}\:\mathrm{sin}\:\mathrm{2x}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{4}+\mathrm{2cos}\:\mathrm{2x}+\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{sin}\:\mathrm{2x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2cos}\:\mathrm{2x}+\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{sin}\:\mathrm{2x}=−\frac{\mathrm{7}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{4cos}\:^{\mathrm{2}} \mathrm{2x}+\mathrm{12sin}\:^{\mathrm{2}} \mathrm{2x}+\mathrm{4}\sqrt{\mathrm{3}}\:\mathrm{sin}\:\mathrm{4x}=\frac{\mathrm{49}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{4}\left(\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{4x}}{\mathrm{2}}\right)+\mathrm{12}\left(\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{4x}}{\mathrm{2}}\right)+\mathrm{4}\sqrt{\mathrm{3}}\:\mathrm{sin}\:\mathrm{4x}=\frac{\mathrm{49}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{8}−\mathrm{4cos}\:\mathrm{4x}+\mathrm{4}\sqrt{\mathrm{3}}\:\mathrm{sin}\:\mathrm{4x}=\frac{\mathrm{49}}{\mathrm{4}} \\ $$$$\Rightarrow\sqrt{\mathrm{3}}\:\mathrm{sin}\:\mathrm{4x}−\mathrm{cos}\:\mathrm{4x}=\frac{\mathrm{49}}{\mathrm{16}}−\mathrm{2} \\ $$$$\Rightarrow\sqrt{\mathrm{3}}\:\mathrm{sin}\:\mathrm{4x}−\mathrm{cos}\:\mathrm{4x}=\frac{\mathrm{17}}{\mathrm{16}} \\ $$

Commented by mnjuly1970 last updated on 23/Apr/23

thanks alot sir cortano ⋛

$${thanks}\:{alot}\:{sir}\:{cortano}\:\cancel{\lesseqgtr} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com