
Question Number 129489 by mr W last updated on 16/Jan/21
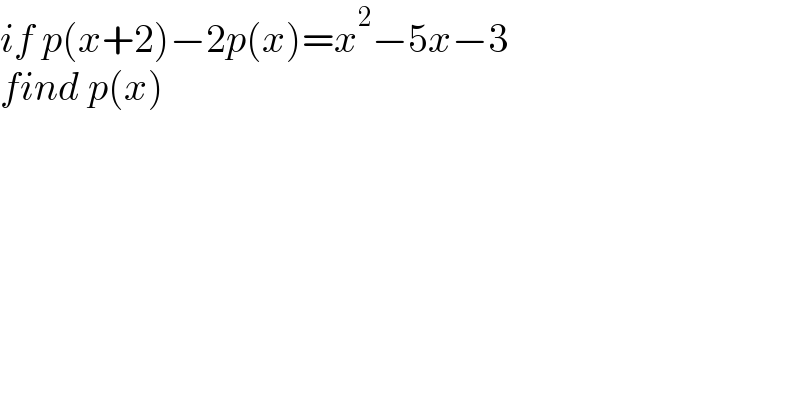
$${if}\:{p}\left({x}+\mathrm{2}\right)−\mathrm{2}{p}\left({x}\right)={x}^{\mathrm{2}} −\mathrm{5}{x}−\mathrm{3} \\ $$$${find}\:{p}\left({x}\right) \\ $$
Answered by bramlexs22 last updated on 16/Jan/21
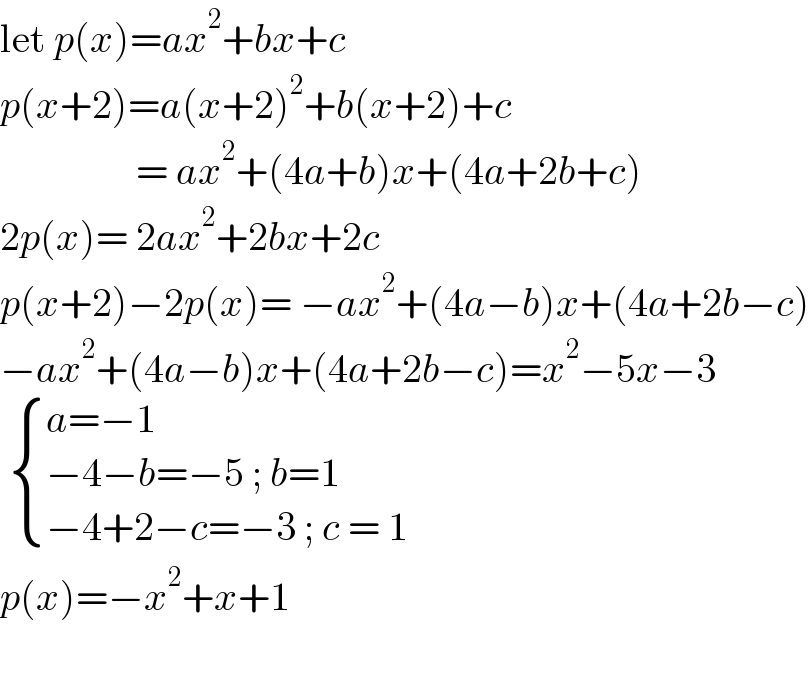
$$\mathrm{let}\:{p}\left({x}\right)={ax}^{\mathrm{2}} +{bx}+{c} \\ $$$${p}\left({x}+\mathrm{2}\right)={a}\left({x}+\mathrm{2}\right)^{\mathrm{2}} +{b}\left({x}+\mathrm{2}\right)+{c} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{ax}^{\mathrm{2}} +\left(\mathrm{4}{a}+{b}\right){x}+\left(\mathrm{4}{a}+\mathrm{2}{b}+{c}\right) \\ $$$$\mathrm{2}{p}\left({x}\right)=\:\mathrm{2}{ax}^{\mathrm{2}} +\mathrm{2}{bx}+\mathrm{2}{c}\: \\ $$$${p}\left({x}+\mathrm{2}\right)−\mathrm{2}{p}\left({x}\right)=\:−{ax}^{\mathrm{2}} +\left(\mathrm{4}{a}−{b}\right){x}+\left(\mathrm{4}{a}+\mathrm{2}{b}−{c}\right) \\ $$$$−{ax}^{\mathrm{2}} +\left(\mathrm{4}{a}−{b}\right){x}+\left(\mathrm{4}{a}+\mathrm{2}{b}−{c}\right)={x}^{\mathrm{2}} −\mathrm{5}{x}−\mathrm{3} \\ $$$$\:\begin{cases}{{a}=−\mathrm{1}}\\{−\mathrm{4}−{b}=−\mathrm{5}\:;\:{b}=\mathrm{1}\:}\\{−\mathrm{4}+\mathrm{2}−{c}=−\mathrm{3}\:;\:{c}\:=\:\mathrm{1}}\end{cases} \\ $$$${p}\left({x}\right)=−{x}^{\mathrm{2}} +{x}+\mathrm{1} \\ $$$$ \\ $$
Commented by mr W last updated on 16/Jan/21
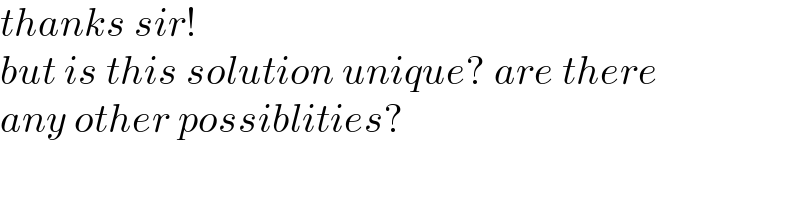
$${thanks}\:{sir}! \\ $$$${but}\:{is}\:{this}\:{solution}\:{unique}?\:{are}\:{there} \\ $$$${any}\:{other}\:{possiblities}? \\ $$
Answered by liberty last updated on 16/Jan/21
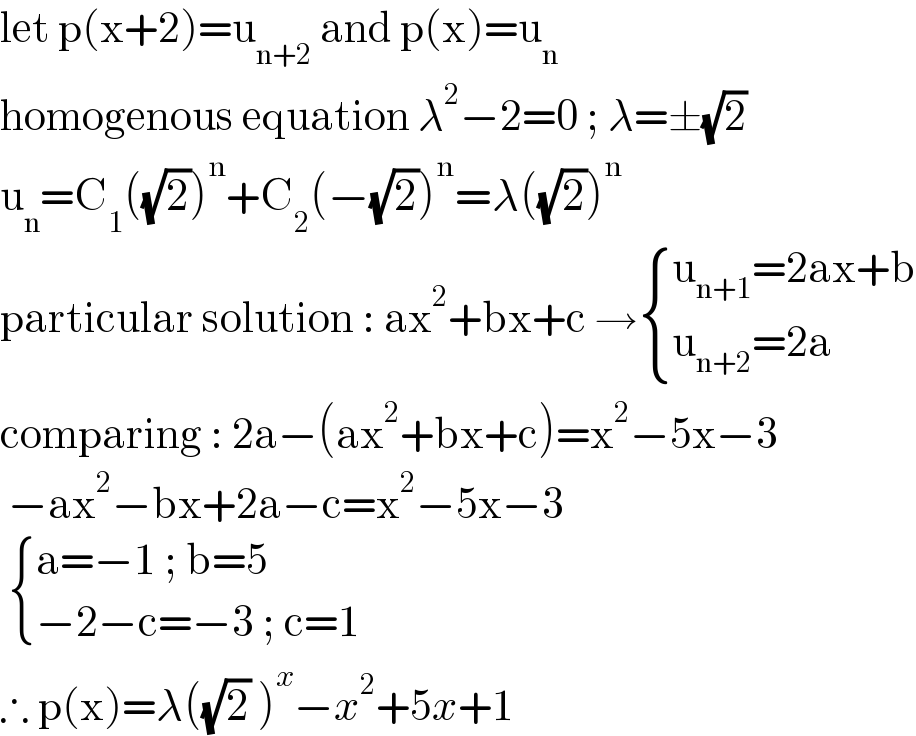
$$\mathrm{let}\:\mathrm{p}\left(\mathrm{x}+\mathrm{2}\right)=\mathrm{u}_{\mathrm{n}+\mathrm{2}} \:\mathrm{and}\:\mathrm{p}\left(\mathrm{x}\right)=\mathrm{u}_{\mathrm{n}} \\ $$$$\mathrm{homogenous}\:\mathrm{equation}\:\lambda^{\mathrm{2}} −\mathrm{2}=\mathrm{0}\:;\:\lambda=\pm\sqrt{\mathrm{2}} \\ $$$$\mathrm{u}_{\mathrm{n}} =\mathrm{C}_{\mathrm{1}} \left(\sqrt{\mathrm{2}}\right)^{\mathrm{n}} +\mathrm{C}_{\mathrm{2}} \left(−\sqrt{\mathrm{2}}\right)^{\mathrm{n}} =\lambda\left(\sqrt{\mathrm{2}}\right)^{\mathrm{n}} \\ $$$$\mathrm{particular}\:\mathrm{solution}\::\:\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c}\:\rightarrow\begin{cases}{\mathrm{u}_{\mathrm{n}+\mathrm{1}} =\mathrm{2ax}+\mathrm{b}}\\{\mathrm{u}_{\mathrm{n}+\mathrm{2}} =\mathrm{2a}}\end{cases} \\ $$$$\mathrm{comparing}\::\:\mathrm{2a}−\left(\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c}\right)=\mathrm{x}^{\mathrm{2}} −\mathrm{5x}−\mathrm{3} \\ $$$$\:−\mathrm{ax}^{\mathrm{2}} −\mathrm{bx}+\mathrm{2a}−\mathrm{c}=\mathrm{x}^{\mathrm{2}} −\mathrm{5x}−\mathrm{3} \\ $$$$\:\begin{cases}{\mathrm{a}=−\mathrm{1}\:;\:\mathrm{b}=\mathrm{5}}\\{−\mathrm{2}−\mathrm{c}=−\mathrm{3}\:;\:\mathrm{c}=\mathrm{1}}\end{cases} \\ $$$$\therefore\:\mathrm{p}\left(\mathrm{x}\right)=\lambda\left(\sqrt{\mathrm{2}}\:\right)^{{x}} −{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{1} \\ $$
Commented by mr W last updated on 16/Jan/21

$${thanks}! \\ $$
Commented by liberty last updated on 16/Jan/21
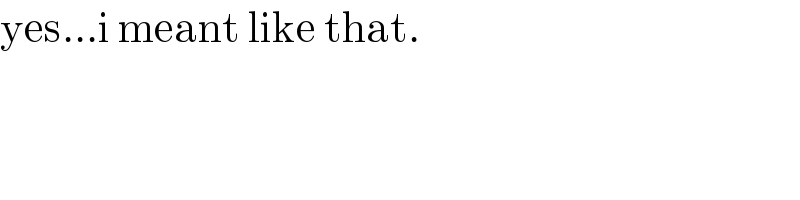
$$\mathrm{yes}...\mathrm{i}\:\mathrm{meant}\:\mathrm{like}\:\mathrm{that}.\: \\ $$
